Interactive Techniques in Three-dimensional Scenes (Part 1): Moving 3D Objects with the Mouse using OpenGL 2.1

Steve Katic

4.97/5 (80 votes)

22 Apr 2009CPOL38 min read

325.3K

25.7K

Moving 3D objects with the mouse using OpenGL.

For easy reference, here is what is covered in the article:

Introduction
Who is this Article for?
Background
Select and Move Process Overview
Virtual Planes based Translation Controller

The Design
Download Source Overview
The Classes
How the Classes are used in the Demo Application
Some Implementation Details
Translation along a Single Axis
Special Case: When the Viewing Plane is Orthogonal to the Virtual Plane
Some Room for Improvement

Using the Demo Project
A Slightly Bigger Picture
Supplementary Information

Shooting a Pick Ray from the Mouse Pointer
OpenGL Picking by Color Code
Ray Plane Intersection Test
OpenGL Modelview Matrix and the Camera Basis Vectors

References
Further Reading

Introduction

There are many applications available for interactive 3D modelling and scene construction that provide the three fundamental manipulation tasks of selecting, positioning and rotating 3D objects. This article describes a strategy used to translate 3D objects with the standard 2D mouse and provides an old fashioned example implementation using OpenGL 2.1 in a C++/CLI Windows Forms application to illustrate the basic principles involved. I've tried to keep it as basic as possible in the hope it can help you create your own implementation.

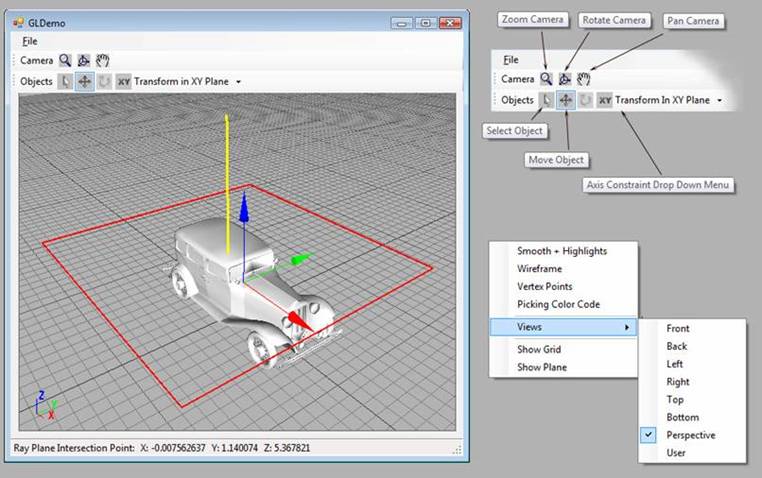
Figure 1: Visual summary of the interaction available in the demo project.

Moving an object is a common task in 3D interactive software that has many scenarios. The demo contains one scenario. This article is about one specific part of the scenario: That part where you left click on the object and drag it to your desired position. Looking at figure 1 above, we have:

Axis Constraint Drop Down Menu: ‘Transform In XY Plane’ is the default selection when you start the application (as shown). The other transform constraint options available in the drop down list are X Axis, Y Axis, Z Axis, XZ Plane or YZ Plane.
Move Object button. Left click on this button to toggle ‘Object Move Mode’ to ‘On’ (A barely visible blue outline on the button indicates ‘On”) “Hey I never said I know how to built interfaces well, did I?”
Left click and drag on an object to select and move it with the mouse cursor. As Michael ‘Jacko’ Jackson would say “This Is It!” Or as I would say “This article shows you how to go about implementing this part”. The object will feel like it’s glued to the mouse cursor as you drag it around in the XY plane, or any other 3D plane or axis you choose to constrain movement to. And you'll pretty much be able to move the object from any sane camera viewing position or angle. (a lot like how you can do it in any good quality 3D modelling package).

This scenario is a combination of WIMP (1 & 2) and Direct Manipulation (3).

There is also another more intuitive scenario that involves Direct Manipulation alone, where an object is moved via a 3-axis widget. I won't be touching this one yet (it might be in part 2 down the track). In Figure 1, the axis aligned triads (one in the bottom left corner of the viewport and one attached to the centre of the object) are not interactive (i.e. not widgets by a conventional UI definition); they just provide visual cues to orientation.

I will be concentrating on the principle on which both these scenarios are based. And that is: The use of axis aligned planes to move a 3D object with the mouse pointer. In the demo, you can watch the plane in action by selecting ‘Show Plane’ from the view context menu (right click anywhere in the viewport to bring up this context menu). If you grab the demo to see it in action immediately (as we all do), but run into problems the Using the Demo Project section may be a good first stop for help.

Who is this Article For?

This article aims to provide a simple, clear and practical description and example to developers, who are not experts in 3D interactive techniques, and would like to implement a 3D translation controller that behaves like it was built by an expert (Of course, you be the judge as to whether that is achieved). The article should at least help get you started with your own implementation. You may feel more comfortable with this article (and download source), with the better knowledge you have of the following:

OpenGL: mainly because the demo source in implemented in OpenGL 2.1, but other APIs can be similarly implemented
Windows Forms and user interface development (The functionality is hosted in a C++/CLI Windows Forms application built in Visual C++ 8.0 on Window Vista and XP)
3D graphics: particularly perspective and orthographic 3D projections, the rendering loop (AKA the so called game loop), and
Some typical strategies for the integration of all the above into an application.

Background

This could be huge, but it’s not going to be. See the Further Reading section for a sample of the background to this topic (or rather the haystack that this needle is in). Continue reading here for the concentrated version. Conventional 3D interactive techniques with the 2D mouse rely on some form of guiding entity or extra abstract object to assist the manipulation of 3D objects. For example, descriptions exist based on the well known idea of a virtual sphere, aka arcball or trackball, to rotate 3D objects. Not so well or as often described clearly enough is the idea of using axis aligned planes and lines of one form or another to translate objects. You can see another implementation in the tutorial article entitled 3D Manipulators using XNA. A survey of literature on 3D interactive techniques indicates that this idea was one of the earliest Direct Manipulation techniques for the translation of 3D objects, and is still the most popular in 3D modelling tools, at least in outward appearances (in the form of some kind of 3-axis translation widget provided to the user), and where implementation details may vary. Today the idea of using planes for translation seems an obvious extension of the idea of a virtual sphere for rotation (whereas over a decade ago it may or may not have been so obvious?).

Select and Move Object Overview

So let’s recap the steps of the process we are interested in, from the user’s point of view (that can be performed in the demo application):

Turn on Move Object Mode: Click on the Move Object button.
Constrain Object Movement: Select the plane from the drop down menu list that object movement will be constrained to.
Select Object: Select the object by moving the mouse pointer over the object and pressing the left mouse button down. Hold the left mouse button down.
Move Object: Move the object by dragging the mouse with the left mouse button down.
Stop Moving Object: Release the left mouse button after the object has been moved.

Our translation controller is initialized at step 3 and used to move the object at step 4 until step 5.

Virtual Plane Based Translation Controller

Here is the implementation in a nutshell. A virtual plane is our guiding entity (virtual as in not visibly rendered to the screen). The plane will be aligned to one of only three possible axis alignments (xy, xz or zy). After an object is selected, the plane is moved to the 3D selection point on the object. Translation is computed by a ray casting procedure which consists of propagating a ray in world space from the viewpoint through the cursor’s position, then testing the intersection between this ray and the plane with each movement of the cursor. The difference between the previous intersection point and the most recent intersection point propagated during this process becomes the displacement vector used to translate the object.

A modular approach is taken in the design so that the translation controller can either be used as a standalone unit or it can be combined with an actual visible guiding entity in the form of a 3D widget (highly recommended) to help reduce the cognitive load on the user during the process and increase the robustness of the implementation.

A detailed description of the virtual plane based translation controller is given below and consists of the following:

The Design
The Code

The Classes
Using the Classes in an Application
Implementation Details
Translation along a Single Axis
Special Case: When the Viewing Plane is Orthogonal to the Virtual Plane
Some Room for Improvement

The Design

Figure 2: The object translation algorithm

A description of the algorithm (Figure 2) is given below.

Select Object: When the user selects an object:

Shoot a ray from m1 to intersect with the object to get the 3D position of the pixel at the intersection point p1.
Align the virtual plane to the axes that the object movement has been constrained to (the XY plane is the example used in the diagram).
Move the height of the virtual plane to the height of p1.

Move Object: When the mouse pointer moves to m1’:

Perform a Ray-Plane intersection test: shooting a ray from m1’ to intersect with the virtual plane to get the intersection point p1’.
Move the object by vector p1’ – p1.
Make p1 = p1’ in preparation for the next movement of the mouse cursor (i.e. for the next iteration through steps 4(a), (b) and (c)).

Note: At step (3c), moving the height of the virtual plane to the height of p1 is important for maintaining a consistent positional correlation of the 2D mouse pointer with the 3D position on the object being moved in views where the perspective projection is applied, and typically not necessary for views that utilize the orthographic projection.

A Special Case

There is one special case the algorithm will need to handle: when the camera/viewing plane is orthogonal to the virtual plane. For more information see the Special Case section.

Download Source Overview

The demo source uses the OpenGL API in a C++/CLI Windows Forms application that has been built in (a) Visual C++ 2008 Professional and Express Edition on Windows Vista and in (b) Visual C++ 2008 Express Edition on XP
There are no reusable packages/components or classes to use (The project contents have not been designed/tested or presented to be used in such a way), and there is very little code required to implement the translation controller anyhow. You might already have things like planes, rays, picking, collision detection and user mouse controls. So the recommended approach is to pick and choose and peruse as many bits and pieces of code and concepts provided, at your discretion.
I wanted to provide a minimal 3D tool environment for you to try out the translation controller in (I like living dangerously,…sometimes). So, the project makes use of a dozen or so DLLs that I use elsewhere (to create a minimal 3D viewing/modelling tool environment for the article) and as long as this strategy works for us they can safely be ignored. There are also a handful of classes in the source, but there are only 3 main classes to concentrate on. They are the MouseTranslationController class, the Ray class, and the Plane class. Other classes (and/or some of their methods) may be mentioned or discussed in so far as how they are involved in the process of (or use case for) moving an object with the mouse, and, how the translation controller is integrated to work in the application. It is hoped that this will help you to produce a clearer mental picture of where you might see the translation controller fitting (or perhaps not fitting) into your application.

The Code (1): Translation Controller Classes Overview

Summary views of the 3 classes (in Ray, Plane and MouseTranslationController) that make up the translation controller are listed below.

MouseTranslationController.h

C++

/// <summary>
/// MouseTranslationController()
/// This class controls how the mouse translates objects in an opengl 3D space
/// However, it currently has one very specific use:
/// It shoots a ray through the mouse location testing for intersections with
/// the an axis aligned plane. It is more of a RayPlaneIntersectionPointFinder
/// than anything else at the moment( and could/should be renamed as such?).
///
/// Vectors and points in 3D space given to this class to manipulate
/// must conform to the flight simulator
/// co-ordinate system and not the OpenGL co-ordinate system.
/// The difference is: The Z axis is vertical in
/// the flight simulator; whereas the Y axis is vertical in OpenGL
/// (This is an inconsistency that
/// could/should be removed ).
/// </summary>
public ref class MouseTranslationController
{
        Ray^ ray;
        Plane^ plane;
        Vector3^ position;             // intersection point of ray on plane.
        DWORD translationConstraint;   // The axes that translation is constrained to

        Vector3^ displacement;
        static Vector3^ lastposition;

        void CreatePlane();
        void CreateRay(int x2D, int y2D);
        void SetPlaneOrientation(DWORD theTranslationConstraint);
        void InitializePlane(DWORD theTranslationConstraint);
        void ApplyTranslationConstraint(Vector3^ intersectPos);
        property Vector3^ PlanePosition;
        property Vector3^ Position;
public:
        MouseTranslationController(void);
        void Initialize(int x2D, int y2D,
                 DWORD theTranslationConstraint,Vector3^ planePos);
        void Update(int x2D, int y2D);
        void DrawPlane();

        property Vector3^ Displacement;
        property DWORD TranslationConstraint;
};

Later we will see that the application directly uses only 3 functions during the move object operation: Initialize( ), Update() and the Displacement property.

Primitives.h

C++

//=====================================================================================
//    Plane defined by a point and a normal
//    The normal and point are expressed in non-opengl Cartesian co-ordinates.
//    where the Z axis in vertical. In opengl the screen and the Y axis is vertical.
//=====================================================================================
public ref class Plane
{
public:
        Vector3^ Normal;
        Vector3^ Position;
        DWORD transformAxes;

        Plane(void);
        Plane(Vector3^ norm,Vector3^ pos, DWORD axes);

        void DrawNormal();
        void Draw()
        property DWORD TransformAxes;
};

//======================================================================================
//      Ray defined by 2 points (can we call it a segment?)
//
//      The 2 points p0 and p1 are expressed in non-opengl Cartesian co-ordinates.
//      where the Z axis in vertical. In opengl the Y axis is vertical.
//======================================================================================

public ref class Ray
{

public:
        Vector3^ p0;
        Vector3^ p1;

        Ray(void);
        Ray(Vector3^ P0,Vector3^ P1);
        Ray(int x2D, int y2D);

        void Generate3DRay(int x2D, int y2D);
        int Intersects(Plane^ p, Vector3^ I);
};

There is nothing particularly interesting in the Plane and Ray primitives, except maybe the Intersects() function, otherwise these classes are much like any other structs/classes typically found to represent a ray and plane.

The Code (2): How the Classes are Used in the Demo Application

Before getting to the code, let’s look at how the TranslationController would typically fit into the application (in informal pseudocode):

The MoveObject process:

Press move object button
Select axis/plane constraint
Select and move object (left mouse button click on object and drag mouse):

OnLeftMouseButtonDown:

Pick an object
InitialiseTranslationController

OnMouseMove:

UpdateTranslationController (generates next 3D displacement vector to move selected object with)
MoveObject (using 3D displacement vector just generated by UpdateTranslationController)

Release left mouse button to stop the process

Here is a little bit more detail about the parameters the translation controller uses:

C++

/// The Translation Controller is initialized with
///     - The current mouse pointer position (to generate a ray from)
///     - A flag indicating the axis or plane that object movement
///       has been restricted to by the user
///     - The 3D ‘hit’ point on the object that was picked.
///       The plane is moved so that this point lies on it.
///       This is the start point of object translation.
TranslationController->Initialize(MousePosition, AxesContraint, 3DHitPoint)

/// The Translation Controller is updated by
///     -passing it the current mouse pointer position
/// It generates the next displacement vector used to move the object to
TranslationController->Update(MousePosition)
///
/// Get the 3d displacement the translation controller just generated and give it to the
/// function that will use it to move the object.
MoveObject(TranslationController->Displacement)

Here is the how the translation controller is actually integrated into the demo. In the implementation Initialize() is called in the render loop and Update() is called when the mouse moves (i.e. in the view panel’s MouseMove() event handler). As for the render loop: typically there tend to be two main options to choose from when deciding where to implement a render loop (AKA the so called game loop) for a graphics API in a Forms Application: In a control’s paint method or in a timer control. The example uses a Timer control. The timer1 code below was generated by dragging a Timer control onto the form in the Designer, setting the Interval property to 1ms and selecting its Tick event to be generated.

C++

this->timer1->Enabled = true;
this->timer1->Interval = 1;
this->timer1->Tick += gcnew System::EventHandler(this, &Form1::timer1_Tick);

/// The rendering loop (or so called Game Loop)
private: System::Void timer1_Tick(System::Object^  sender, System::EventArgs^  e)
{
     DrawView();
}
void Form1::DrawView()
{
    m_OpenglView->DrawFrame();
    ...
    ...
    if(m_OpenglView->PickSelection)
    {
         PickAnObject();
         InitTranslationController();
         // switch off picking
         m_OpenglView->PickSelection = false;
         // we do not render this pass
         return;
    }

    // Draw stuff
    ...
    ...
    m_OpenglView->SwapOpenGLBuffers();
}

And the MouseMove Event handler:

C++

private: System::Void view1_MouseMove
         (System::Object^  /*sender*/, System::Windows::Forms::MouseEventArgs^  e)
{
        // ultimately calls...
        translationController->Update((int)Mouse2DPosition->X,(int)Mouse2DPosition->Y);
        m_scene->MoveSelectionSetDelta(translationController->Displacement);
        // where Mouse2Dposition contains the X and Y properties of the MoseEventArgs e
}

The Code (3): The Implementation Details

STEP 1: Pick an Object

3(a) Shoot a ray from m1 to intersect with the object to get the 3D position of the pixel at the intersection point p1 is performed by the forms PickAnObject() function. If an object has been picked, the position on the object that the ray hit the object is stored the form’s Mouse3dPickPosition property. Color coded picking is the strategy used to select an object (any picking strategy can be used). The object’s color is used to identify and select the picked object (Note: you may be aware that the GetPixelColorAnd3DPostion() function breaks some rules of ‘good’ programming practice, but hopefully at least, its name does convey its purpose).

C++

void PickAnObject()
{
        m_scene->DrawObjectsInPickMode();
        array<unsigned char>^ color =
                 GetPixelColorAnd3DPosition(Mouse3DPickPosition,
                 (int)Mouse2DPosition->X,(int)Mouse2DPosition->Y);
        m_scene->SelectPickedModelByColor(color);
}

STEP 2: Initialize the Translation Controller

3(b) the alignment of the virtual plane and 3(c) the adjustment of the height of the plane to p1 is performed in the translation controller Initialize() function.

C++

void Initialize(int x2D, int y2D, DWORD theTranslationConstraint,Vector3^ planePos)
{
    ray->Generate3DRay(x2D, y2D);
    PlanePosition = planePos;
    Position = planePos;
    LastPosition = Position;
    Displacement = Vector3::Zero();
    InitializePlane(TranslationConstraint);
}

As shown below, the parameters passed to the function when it is called, are:

The current mouse position Mouse2DPosition->X, Mouse2DPosition->Y
The axis/plane the user selected for object movement to be constrained to (m_CurTransformationAxes stores an enumerated identifier), and
The 3D position on the object that had just been picked in PickAnObject()

void InitTranslationController()
{
    if(m_scene->PickedModel != nullptr)
        translationController->Initialize((int Mouse2DPosition->X,
        (int)Mouse2DPosition->Y, m_CurTransformationAxes, Mouse3DPickPosition);
}

Let’s split a hair or two for a moment. If you recall we said earlier that the height of the virtual plane is set to the height of picked point. This is a minimum requirement of the design. In the implementation, however, the picked point is the point used to define the virtual plane. The main reason for this is simply to render a small movable portion of the [infinite] virtual plane centred at this point (for a bit of visual feedback of what’s happening).

STEP 3: Update the Translation Controller

4(a) The Ray-Plane intersection test is performed in translationController Update(). The 2D mouse position on the screen is passed to this function. The mouse ray in propagated; the intersection point of the mouse ray with the virtual plane is found; the intersection point is modified based on axis constraints; and the point defining the plane and displacement vector are updated.

C++

void Update(int x2D, int y2D)
{
     Vector3^ intersection = Vector3::Zero();
     ray->Generate3DRay(x2D, y2D);
     ray->Intersects(plane,intersection);
     ApplyTranslationConstraint(intersection);
     PlanePosition = Position;
     Displacement = Position - LastPosition;
     LastPosition = Position;
}

ApplyTranslationConstraint() may seem more complex that it actually is. If you look at it in the source code you will see that all it does is generate the new object translation position a little differently when translation is restricted to one axis only: basically the position is only updated along that one axis to which translation is restricted.

For completeness here is the call:

C++

void UpdateTranslationController()
{
    translationController->Update((int)Mouse2DPosition->X,(int)Mouse2DPosition->Y);
}

Once the Move Object operation has started, Update() continues to be called each time the mouse is moved, generating a new incremental displacement vector, until the left mouse button is released.

STEP 4: Move the Object

The displacement vector generated by Update() is used to translate the object.

C++

m_scene->MoveSelectionSetDelta(translationController->Displacement);

This is handled by the viewport control’s MouseMove event handler (m_OpenglView is our viewport that inherits from Panel). So each time the mouse moves (in Object Move Mode with left mouse button down) the Scene::MoveSelectionSetDelta() function is ultimately called (it is buried down a bit in other functions as shown in the snippet below).

C++

// in Form1.h

m_OpenglView->MouseMove += gcnew System::Windows::Forms::MouseEventHandler
                                            (this, &Form1::view1_MouseMove);

view1_MouseMove();
       calls --> ProcessMouseMove();
              calls -> EditModeMouseMove()
                      calls ->
                               UpdateTranslationController();
                               m_scene->MoveSelectionSetDelta(); 
void Scene::MoveSelectionSetDelta(Vector3^ deltaV)
{
      if(deltaV == nullptr)return;
      UpdateSelSetWorldPos(deltaV->X, deltaV->Z, deltaV->Y);
}

Translation along a Single Axis

Not a great deal of attention (code wise) has been paid to translations along a single axis apart from just nullifying (setting to zero) the translation values in the other two axes and rotating the virtual plane around the axis (of translation) to be ‘more parallel’ with the viewing plane (in order to minimize the likelihood of user disorientation during the move operation, particularly when the mouse pointer is not moved along the single 3D axis). The virtual plane is rotated so that it is parallel or ‘co-planar’ with the viewing plane with respect to the other two (non-translation) axis components (as shown in the diagram below).

Figure 3: Translation along a single axis

The diagram shows an example of the process where: for translations along the single axis Y, the X and Z components of the plane’s normal are set to the X and Z values of the initial intersecting (or pick) ray. This has the effect of rotating the plane around the Y axis so that the plane’s local XZ components are parallel/co-planar with the local XZ components of the viewing plane (in views with orthogonal* projections). The code for this is in the translation controller’s SetPlaneOrientation() function.

An alternative method of using lines to handle translation along a single axis can be found in the tutorial article entitled 3D Manipulators mentioned previously (in the Background section of the article).

*Note: A ray cast from the mouse into a view with perspective projection applied, typically is not orthogonal to the viewing plane (but it’s usually close in our case). In contrast, (and at the risk of stating the obvious) the ray cast into a view with orthogonal projection is always orthogonal to the viewing plane.

The Special Case

Figure 4: Special case instances

There is a special case that needs to be handled: when the viewing plane is orthogonal to the virtual plane in a view that has an orthographic projection applied to it. The Ray-plane intersection test fails because the virtual plane’s normal is perpendicular to the ray and thus the ray will not intersect the plane. There are 12 possible instances when this special case can occur (Figure 4). The most obvious solution is to align the virtual plain to the axes that most appropriately matches the movement constraint and state of the viewing plane for translation to occur. We could use a process of elimination to find this alignment: where the virtual plane is aligned to each of the 3 possible axes alignments and performing the intersection test until the test does not fail. In the best case scenario, we can perform the test once and in the worst case scenario it is performed 3 times. For a worst case example: Suppose the user has constrained the translation to the x axis. The intersection test will fail for the ray with the plane aligned to the XY axes and YZ axes, and succeed for the XZ axes. Using the process of elimination can also end up being the least efficient strategy in the worst case.

We can validate the input early to reduce unnecessary processing. That is, we obtain the position/orientation of the viewing plane and align the virtual plane to the axes that ensure it is parallel to the viewing plane; this ensures the intersection test will succeed. It is a simple solution, if a somewhat tedious one.

Here are two ways of accessing the state of the viewing plane:

We could get it abstractly: via a camera class/object if we have one or via custom transformation/viewing matrix states built on top of OpenGL 3.0, or
We could get it directly via the current state of the opengl (pre 3.0) modelview matrix. The demo source uses the latter method (accessing the modelview matrix), in the translation controller’s InitializePlane() function. For more information, see OpenGL Modelview Matrix and the Camera Basis Vectors in the supplementary section.

Some Room for Improvement

There is always room for improvement. Here are just some possible options:

The TranslationController classes (MouseTranslationController, Ray and Plane) require points and vectors where the z coordinate axis is vertical. In OpenGL the Y axis is vertical. This inconsistency could be removed if you are opengl ‘centric’ (Otherwise leave as is, in its more generic form, for use with other APIs… like what, DirectX?). If you don't understand this point, you can safely ignore it.
It feels like a few optimizations can be made, but I don't know what they would be, so I'll leave that to you.

The translation controller has not been integrated into the demo application for efficiency:

Where Update() continues to be called via the MouseMove handler, it may be more logically correct to pick an object and initialize the translation controller in a MouseDown event handler instead of in the render loop (where it is like ‘once removed’ from the direct input event handler).
Explore Rendering loop options: This is probably more of an investigative issue than an improvement. We use a System.Windows.Forms.Timer Control as our so called game loop. Another popular option (that I haven't tried with this implementation) is to inherit from a Forms Control (e.g. Panel control), then override and use the control’s Paint method as the so called rendering loop. In both these cases, the code is executed using the application's UI thread. The UI thread is an obvious first choice and testing showed the most computationally expensive part of the algorithm to be the continual ray-plain intersection test (where a frame may take 1.67 ms to render [approx 60fps] and vary, the intersection test can take 0.06 ms). Yet another option is to use multithreading. There are 2 other timers that can be used in this case: System.Timers.Timer and System.Threading.Timer if you think you need them (like people at Intel would).
OpenGL 3.0. If you feel the need to be proactive and OpenGL 2.1 is too old fashioned for you, then it is likely you would want to implement this design via the programmable pipeline (i.e. shaders); do stuff like store or derive your own matrix versions/states to suit your particular implementation requirements. The demo uses as much as possible of what opengl offers (fixed pipeline or not): The more that is off loaded to the OpenGL API means less code for us to write ( a simple and perhaps fatal approach? But hopefully you should be able to get the gist of this article despite the implementation).
I've reviewed and re-reviewed this article to eliminate errors (ad infinitum). But it’s never as good as a peer review (i.e. someone else's pair of eyes reviewing it; you know, like software testing: you don't want your programmer testing his own program if you can avoid it- he/she/I can tend to be instinctively biased apparently). So if you notice any errors (blatant or otherwise misleading) or have suggested improvements to benefit other readers, let us know.

Using the Demo Application

What You Must Know

The computer system’s color resolution must be set to 32 bit (High) for the color code picking to work.
.NET Framework (at least 2.0) must be installed on your system.

What You Should Know (About the User Interface)

The picture below shows:

A screenshot of the demo with a 10 X 10 portion of the current virtual plane and plane normal. Its visibility can be toggled with the ‘Show Plane’ context menu item.
Top right of screenshot shows the Camera menu strip and Objects menu strip. The slightly visible blue border around the Move Object button indicates it is currently active.
Bottom right of screenshot shows all the viewing options available on the context menu. Right mouse click in the viewport and the context menu appears for you to select an option.

Figure 5: Visual summary of the interaction available in the demo project.

To move an object with the mouse:

Click on the Move Object button on the Object menu strip to turn on Move Object mode.
Select the plane/axis (you want to constrain object movement to) from the axis constraint drop down menu list.
Select the object by moving the mouse pointer over the object and pressing the left mouse button down. Hold the left mouse button down.
Move the object by dragging the mouse with the left mouse button down.
Release the left mouse button after the object has been moved.

On the File menu, you will find 2 options:

Open: allows you to load 3ds, obj, x or im model files from a file open dialog box.
New: clears all the models in the current scene.

Tips (because of limitations in the application):

The camera will always be pointing to the origin so do not pan the camera too far from it for the best viewing experience (when rotating the camera around).
There is one model supplied for viewing. If you decide to load some other models beware: the application will not zoom to its extents or location when you load it. So you may have to manually zoom or move the camera to see very large/very small models or models not located near the origin.
Zooming: Click on the zoom button on the Camera menu strip. Drag the mouse vertically in the viewport to zoom in/out (with left mouse button down). Note: It is not true zooming (of the fov), but a translation (dolly) of the ‘camera’ backwards and forwards that produces the zooming effect.
Rotating: Click on the rotate button on the Camera menu strip. Drag the mouse around in the viewport with left mouse button down to get a feel for how it rotates. The ability to roll the camera is not implemented.
Panning: Click on the pan button on the Camera menu strip. Again, drag the mouse around in the viewport with left mouse button down to get a feel for how it pans.
If you lose sight of your object in the application (yes, unfortunately, you can lose it!) just do File->New to clear the scene and File->Open and reload an object (A reset button would be better, but...?).

What You Might Like to Know

The appropriate DLLs have been included with the demo package enabling it to also run on Windows XP as well as <place>Vista.

The system it was built on (system 1):

Windows Vista (service pack 1)
.NET Framework 2.0 (minimum)
512 MB Radeon HD 4850
32 bit (High) color resolution setting
AMD Athlon(tm) 64 X2 Dual Core Processor 4400+ 2.3GHz, 2GB RAM

Another system it was built and tested on (system 2):

Windows Vista (service pack 1)
.NET Framework 2.0 (minimum)
256 MB Radeon X1950 Pro
32 bit (High) color resolution setting
AMD Athlon(tm) 64 X2 Dual Core Processor 4400+ 2.3GHz, 1GB RAM

An [old] system it was tested on (system 3):

Windows XP ( with service pack 3)
.NET Framework 2.0 (minimum)
32 MB geforce2 (mx 200)
32 bit (High) color resolution setting
AMD 3.0 GHz, 512 MB RAM

You could assume that the closer your system specs are to system 1 the better it will run. There is a noticeable time lag between the mouse movement and object movement on the older test system (system 3), probably making the translation controller, in its current form on that system, unusable for practical purposes.

A Slightly Bigger Picture

The translation controller only controls the translation of complete single objects in the global 3D space/coordinate system with the mouse. There are also these issues to consider:

Translating in the local 3D space/coordinate system
Using direct manipulation widgets to translate or manipulate objects
Selection/positioning of sub elements/ sub sets of objects (sub-object, mesh, polygons, vertices)
Using multiple viewports (like 4) to maintain/enhance the users orientation in the application’s 3D space (the cognitive burden on the user to mentally visualize what is occurring during some manipulations is just too big with only one viewport, especially at some of the special case instances where the full nature of the translation upon an object is not apparent). This ‘cognitive overload’ is probably the major factor that motivates 3D interactive application researchers to seek new solutions.
Move an object to a position via dialog box(es) (WIMP based interface option)
Investigate implementing some functionality on the gpu/programmable pipeline/OpenGL 3.0 (e.g. in a shader: would there be any advantage/disadvantage to implementing parts of this in a shader?)
Interactive 3d techniques applied to other fundamental object manipulations (i.e. rotation and scaling)
For an even bigger picture, see the Further Reading section at the end of the article.

Supplementary Information

This section contains information that was produced in the writing of this article. The topics would be familiar to most experienced programmers who would have seen them covered in one form or another before (so feel free to criticize). Thus, it may be particularly more useful to beginners and the not so experienced.

Shooting a Pick Ray from the Mouse Pointer
OpenGL Picking by Color Code
Ray Plane Intersection Test
OpenGL Modelview Matrix and the Camera Basis Vectors

Shooting a Pick Ray from the Mouse Pointer

The diagram below shows a snap shot of shooting a pick ray out from the mouse pointer.

Point p0 lies in the near clipping plane (also referred to the viewing plane in the article), while p1 lies in the far clipping plane. The 3D points p0 and p1 are generated using the 2D xy position of the mouse pointer on the screen and the z values of 0 for the near clipping plane, and 1 for the far clipping plane respectively. The code that shoots the ray from p0 to p1 is shown below. Note that the swapping of the Z and Y values shown at the end of the function is usually not required. In our case p0 and p1 are required to be in flight simulator co-ordinate form because the next function in the process (i.e. the Intersects function) requires them to be in that form.

C++

void Generate3DRay(int x2D, int y2D)
{
       if(p0 == nullptr)
               p0 = Vector3::Zero();
       if(p1 == nullptr)
               p1 = Vector3::Zero();
       int x =x2D;
       int y =y2D;
       GLint viewport[4];
       GLdouble modelview[16];
       GLdouble projection[16];
       GLdouble winX, winY;
       GLdouble winZ0 = 0.0f; GLdouble winZ1 = 1.0f;
       GLdouble posX0, posY0, posZ0;
       GLdouble posX1, posY1, posZ1;
       glGetDoublev(GL_MODELVIEW_MATRIX, modelview);
       glGetDoublev(GL_PROJECTION_MATRIX, projection);
       glGetIntegerv(GL_VIEWPORT, viewport);
       winX = (GLdouble)x;
       winY = (GLdouble)viewport[3] - (GLdouble)y;
       glReadBuffer( GL_BACK );
       gluUnProject( winX, winY, winZ0,
                 modelview, projection, viewport, &posX0, &posY0, &posZ0);
       gluUnProject( winX, winY, winZ1,
                 modelview, projection, viewport, &posX1, &posY1, &posZ1);
       // swap opengl co-ordinates back to NASA flight simulator co-ordinates
       p0->X = (float)posX0;
       p0->Y = (float)posZ0;
       p0->Z = (float)posY0;
       //
       p1->X = (float)posX1
       p1->Y = (float)posZ1;
       p1->Z = (float)posY1;
}

OpenGL Picking by Color Code

Picking can be implemented a number of ways. In our example color coded picking is used. When an object is loaded into the scene it is assigned its own wireframe color (i.e. this is the color of the objects wireframe when drawn in wireframe mode). Before picking takes place each object in the scene is drawn with this color as shown below. Picture (a) shows normal rendering of the models in textured and wireframe mode. Picture (b) shows how the objects are rendered for color coded picking.

(a) textured and wireframe rendering

(b) rendering for color coded picking

The color coded rendering is performed by the scene’s DrawObjectsInPickMode() function in PickAnObject() where objects are not rendered to the screen. The actual rendering code is out of the scope of this article, so for more information about OpenGL color coding for picking you can go here. The picking code is provided below:

C++

///
/// GetPixelColorAnd3DPosition() returns the current 3d position and
/// color of the 2D pixel at (x,y)
/// using the current viewport, projection and modelview data that defines our (camera's)
/// view into the 3D world. It is only used to pick objects in 3D space.
///
array<unsigned char>^ GetPixelColorAnd3DPosition(Vector3^ positionOut,int x, int y)
{
        static GLint viewport[4];
        static GLdouble modelview[16];
        static GLdouble projection[16];
        GLfloat winX, winY, winZ;
        GLdouble posX, posY, posZ;
        glGetDoublev(GL_MODELVIEW_MATRIX, modelview);
        glGetDoublev(GL_PROJECTION_MATRIX, projection);
        glGetIntegerv(GL_VIEWPORT, viewport);
        GLubyte pixel[3];
        winX = (float)x;
        winY = (float)viewport[3] - (float)y;
        glReadBuffer( GL_BACK );
        //read color and depth
        glReadPixels(x, int(winY),1,1,GL_RGB,GL_UNSIGNED_BYTE,(void *)pixel);
        glReadPixels( x, int(winY), 1, 1, GL_DEPTH_COMPONENT, GL_FLOAT, &winZ );
        gluUnProject( winX, winY, winZ, modelview, projection,
                          viewport, &posX, &posY, &posZ);

        positionOut->X = (float)posX;
        positionOut->Y = (float)posZ;
        positionOut->Z = (float)posY;
        array<unsigned char>^ color = gcnew array<unsigned char>(3);
        color[0] = pixel[0];
        color[1] = pixel[1];
        color[2] = pixel[2];
        return color;
}

Ray Plane Intersection Test

This is not a tutorial showing you how to perform a ray-plane Intersection, but rather a brief description of the thought process that was involved in understanding the code that is used in the application. ‘Real and proper’ ray/plane information can be found by following the links in the references section at the end of the article. The Algebraic approach is taken using basic arithmetic and vector addition (and applies equally well to 2D and 3D vectors)

What We Have

A ray: defined by 2 points p0 and p1.
A Plane: defined by a normal vector n and a point in the plane V0.

What We Should Know

The two nonzero vectors a and b are perpendicular if and only if the dot product a.b = 0. (Here we have the choice of either going deeper into the realm of simple theorem proofs of trigonometry and pythagoras to convince ourselves how and why this is so, or we could just have faith in our mathematicians and accept it as a rule that can be useful to us in many ways. What follows next is an application of its usefulness)
The dot product a.b = 0 is one way of defining a plane in space. By thinking of one of the vectors as the normal of a plane (let’s say the vector a is now the normal), then all of the vectors b that satisfy the dot product equation sit in a particular plane. Obviously this also means that all the pairs of points used to define a vector b also lie in that plane.

Vectors

A vector can be thought of in two ways: either a point at <x,y,z> or a line going from the origin <0,0,0> to the point <x,y,z>.

w = P0-V0
v = V1-V0
u = P1-P0

Looking at the diagram with basic vector math knowledge, we see that:

w + su = v (3)

Because the aim is to get an answer in point form the following expression (aka definition of a line) is usually used as the final equation to solve:

P0 + su = V1 (4)

This can be thought of as ‘move the start point P0 by the vector su to get to the end point V1, where s is usually described as some scalar value (s can be thought of as (some scalar value that when multiplied by u represents) the portion (i.e. shorter piece) of u that ends at the intersection point V1).

We have P0 and u, but s is missing.

Here is how s is usually found:

Applying (1) and (2) to the problem where v is perpendicular to N (and . represents the dot product)

N.v = 0

We substitute the value of v from (3) to obtain

N.(w + su) = 0
=> N.w + N.su = 0

Use the fact that the dot product is commutative (i.e. N.su is the same as sN.u)

=> N.w + s(N.u) = 0
=> s(N.u) = -N.w
=> s = -N.w/N.u

For the code version of this algorithm presented below:

let D = N.u and N = -N.w. Then s = D/N, and
the final equation to solve from (4) is expressed as intersectPoint = p0 + s*u

C++

//=======================================================
// Intersects(): intersect a segment and a plane
//    Input:  p = a plane
//    Output: I = the intersection point (when it exists)
//    Return: 0 = disjoint (no intersection)
//            1 = intersection in the unique point I
//            2 = the segment lies in the plane
//
// Adapted from:
// http://www.softsurfer.com/Archive/algorithm_0104/
// algorithm_0104B.htm#Line-Plane%20Intersection
//
//=======================================================
int Intersects(Plane^ p, Vector3^ I)
{
     Vector3^ intersectPoint;
     Vector3^ u = p1 - p0;
     Vector3^ w = p0 - p->Position;
     float     D = p->Normal->Dot(u);
     float     N = -p->Normal->Dot(w);
     if (Math::Abs(D) < ZERO)      // segment is parallel to plane
     {
          if (N == 0)               // segment lies in plane
                return 2;
          else
                return 0;           // no intersection
     }
     float s = N / D;
     if (s < 0 || s > 1)
         return 0;                  // no intersection
     intersectPoint = p0 + u*s;     // compute segment intersect point
     I->X  = intersectPoint->X;
     I->Y  = intersectPoint->Y;
     I->Z  = intersectPoint->Z;
     return 1;
     }

OpenGL Modelview Matrix and the Camera Basis Vectors

Even though there is no camera as far as OpenGL is concerned, it is useful to think of the modelview matrix as where you stand with the camera and where you are pointing it. This makes the handling of the special case in our implementation (i.e. when the viewing plane is orthogonal to virtual plane of constraint) a little more simple, even if somewhat tedious to arrive at. If you are performing scaling that may affect the modelview matrix, it may be a good idea to store the orientation values it contains before the scaling is applied to it (Since the deprecation of the fixed pipeline in OpenGL 3.0 encourages the developer to implement all there own matrix manipulations, it seems storing the various states of particular matrices you may need is now obligatory).

In our old fashioned OpenGL 2.1 example no scaling is performed that effects the opengl modelview matrix, so we grab the ‘camera basis vectors’ directly from the modelview matrix as is. Also the camera cannot roll: this also helps, as we shall soon see. The elimination of scaling and rolling is deliberate (If I were in OpenGL 3.0 I would store a matrix similar to this state specifically for the special cases in the implementation).

Here is how we find out where the camera is currently pointing (i.e. its pitch, yaw and roll). Suppose we retrieve the modelview matrix like so:

C++

GLdouble m[16];
glGetDoublev(GL_MODELVIEW_MATRIX, m);

Then if we describe the matrix like this:

The following sub matrix contains the basis vectors that provide us with the orientation of the camera.

Where the basis vectors (are often called the) RightVector [Rx, Ry, Rz], UpVector [Ux, Uy, Uz] and LookAtVector [Ax, Ay, Az] are shown in the diagrams below. The second diagram is an example to get (re-)orientated: It shows the state of the camera rotation sub-matrix when the camera is in the front view position (a typical initial state with no rotations applied; pitch, yaw and roll all equal zero; and it is the Identity matrix).

Camera/viewing plane basis vectors

Camera basis vector matrix in Front View

How This Helps Us

Once we have this knowledge, it is simple to check the orientation of the camera and make some decisions based on it. The tedious part is finding the minimal number of the most convenient variables (out of the nine in the sub matrix) to check in order to find the camera orientation. Another feature (or rather lack of) of our camera that helps us is the fact that the camera does not roll (around its LookAt vector), it can only pitch (around its Right vector) and yaw (around its Up vector). Here is what we can end up with:

C++

if (m6 == 1 or -1 )// Up vector z component
{
    Camera is viewing from the top or bottom
}
else if (m6 == 0)// Up vector z component
{
    Camera is viewing from front, back, left or right
    if(m8 == 0) // LookAt vector x component
        Camera is viewing from back or front
    else if(m8 == 1 or -1) // LookAt vector x component
        Camera is viewing from left or right
}

We can confirm this as a reasonable solution by looking at the composition of the basis vector submatrix for the camera. In keeping to the old fashioned theme (i.e. opengl 2.1) our camera is also a basic old fashioned one. The following functions are used to rotate the camera so that the modelview matrix is multiplied by them with the product replacing the current matrix.

And note that since rolling is not currently implemented, the last function glRotate*(a,0,0,1) is ignored (thus z is always 0). As you will see, this fact will be used to our advantage.

After the rotations are applied to the modelview matrix, the (de)composition of the basis vectors can be expressed in the following way:

Where x is the camera’s pitch angle, y is the camera’s yaw angle, and z is the camera’s roll angle.

Then through observation and a little analysis, the following correlations between elements in the modelview matrix and the camera orientation were discovered and used:

Camera pitch of 90 or -90 degrees from the Front View (Identity position). The key here is that the camera cannot roll (around the LookAt vector). This means z = 0 degrees is an invariant (does not change from its original value in the front view (identity matrix). Thus substituting Sin(z) = Sin(0) = 0 and <place>Cos(0) = 1 into the composition of m6 simplifies it to Sin(x). Note that x is the pitch of the camera in degrees relative to the identity pitch (when the camera is in the front view position) and is independent of the global axes. That is, it works for the camera pitching to the Top View from any arbitrary position/orientation of the camera. The example below illustrates the case of the camera rotating around the global X axis from the Front View to the Top View.

An example: the camera manipulated to the Top View position that results in a 90 degree pitch of the camera.

Camera pitch of 0 from the Front View (Identity position); That is, the camera viewing plane is orthogonal to the XY plane; the fact that the camera cannot roll is used again here to give us m6 = Sin(x). So m6 = 0 when the camera is not pitched at all.

It can still rotate (or yaw) in the XY plane while m6 = 0, so finally we need to test for when the camera viewing plane is orthogonal to the YZ plane (back, front view) and XZ (left, right view).
Arbitrary camera yaw angle. m8 (Ax) = sin y.

This time we use the actual sine of the angle of orientation of the camera as it rotates around the Z axis (opengl y axis) in the XY plane. So in the front view (0 degrees) and back view (180 degrees) m8 = 0, at the left view (90 degrees) m8 = 1 and right view (-90 or 270 degrees) m8 = -1.

That will handle the orthogonal views (front, back, left and right) in the XY plane. For example, when the camera is at the Left (or Right) View and the object translation is restricted to the XY plane, we flip the plane to the YZ plane position and restrict the object translation to the Y axis only. Similarly for the camera at the Front (or Back) View, where the object translation is restricted to the XY plane, we flip the plane to the XZ plane position and restrict the object translation to the X axis only.

What we haven't yet handled are all the arbitrary cases in between the orthogonal views when the camera rotates around the Z axis that points upwards (opengl y axis). Here is how: Basically if the yaw is less than 45 degrees around from the orthogonal view for the back and front views, the plane is flipped to the XZ alignment and object translation is restricted to the X axis. And when the yaw is less than 45 degrees around from the left or right view (yellow in the diagram), the plane is flipped to the YZ alignment and object translation is restricted to the Y axis.

This idea ends up as the following code implementation (in the TranslationController’s InitializePlane() function):

C++

if((modelview[8] <= 0.7071f && modelview[8] >= -0.7071f)) //front or back view
{
        if(theTranslationConstraint == XYTRANS || theTranslationConstraint == XTRANS)
        {
               newAlignment = ZXTRANS;
               newTranslationConstraint = XTRANS;
        }
        else if(theTranslationConstraint == YZTRANS ||
                       theTranslationConstraint == ZTRANS)
        {
               newAlignment = ZXTRANS;
               newTranslationConstraint = ZTRANS;
        }
}
else if((modelview[8] <= -0.7071f ||
              modelview[8] >= 0.7071f))// left view or right view
{

        if(theTranslationConstraint == XYTRANS || theTranslationConstraint == YTRANS)
        {
               newAlignment = YZTRANS;
               newTranslationConstraint = YTRANS;
        }
        else if(theTranslationConstraint ==
              ZXTRANS || theTranslationConstraint == ZTRANS)
        {
               newAlignment = YZTRANS;
               newTranslationConstraint = ZTRANS;
        }
 }

References

This article actually tries to simplify and expand on the somewhat convoluted description I gave here. This article is still not as simple as I want, but I hope it has helped you.

Ray Plane Intersection
OpenGL General
- http://www.opengl.org/wiki/index.php/Common_Mistakes
OpenGL Color Coded picking
- http://www.lighthouse3d.com/opengl/picking/index.php3?color1

History

7^th April, 2009: Initial post
9^th April, 2009: Minor changes to article

License

This article, along with any associated source code and files, is licensed under The Code Project Open License (CPOL)