Table of Contents
- Introduction
- AI Search Methods for Sliding Puzzle
- Implemented Program
- Implemented Complementary Programs
- Results
- Conclusion
- Acknowledgement
- References
- Appendix
1. Introduction
Basic search algorithms constitute the fundamentals of Artificial Intelligence (AI). So learning their concept and being able to implement them are extremely crucial to do more advanced research on AI.
In this report I will be explaining the details of my solution algorithms, implemented programs, and the results I have concluded.
2. AI Search Methods for Sliding Puzzle
The very basics of almost anything related to AI can be found in the book of Steward Russell and Peter Norvig; “Artificial Intelligence: A Modern Approach” [1].
In this take home examination, we were asked to implement Breadth First Search (BFS), Depth First Search (DFS), Iterative Deepening Depth Limited Search DFS (IDFS), and A* algorithm with “Misplaced Tiles Heuristic” (A* Mis) and “Total Manhattan Distance Heuristic” (A* Man) on an adjustable size “Sliding Puzzle”. Among these algorithms, A*, IDFS, and BFS give optimal paths, on the other hand, DFS is not optimal in the sense of detecting the shortest solution path.
Sliding puzzle requires an agent to solve the problem, which is the program written by us in that take home examination. It is a deterministic, episodic, and fully observable problem. In other words, it is one of the simplest problems to realize in the computer environment. However, sliding puzzle has a very loopy structure. The smallest loop is constructed at only two steps, i.e., moving a tile forward and backward. Although finding that two step loop is very easy, some larger loops are not trivial to detect.
While solving this puzzle, a history of opened states should be constructed. Otherwise, the search space unboundedly expands and solving even the easiest puzzles becomes a burden and sometimes impossible. I kept that history in a Sorted List structure of C#. It basically sorts the inserted nodes with a key and when asked to retrieve a node, the node is requested with that key. So search in the history becomes very efficient and fast.
For further reference, a 3x3 sliding puzzle has 181,440 solvable states, a 4x4 one has ~13 trillion steps, and a 5x5 case has ~1025 states. So, 3x3 is almost the only one that can be solved with all algorithms in a reasonable time.
The best way to explain a written code is to draw its flowchart. So I will be explaining the algorithms used with the flowchart. Hopefully, they will make this report easier to understand and more clear.
I will be explaining my methods in more detail in the corresponding sections in this report.
2.1. Implemented Uninformed Search Methods
Uninformed search, as the name implies, has no idea to visit which successor node would be beneficial. BFS, DFS, and IDFS are the ones that are implemented in this take home examination.
2.1.1. Breadth First Search (BFS)
The implemented algorithms are exactly the same as explained in [1] except the history keeping. BFS algorithm also works without history, but due to the loopy structure of the sliding puzzle, the search space becomes unbounded. Hence, filling up the memory before the solution is found to become extremely possible. On the algorithm tests, it is seen that BFS cannot solve puzzles exceeding 15 steps in a reasonable time (2-3 minutes). However, after implementing history, it can reach to 25 steps in a reasonable time. My BFS always gives an optimal (shortest) solution path.
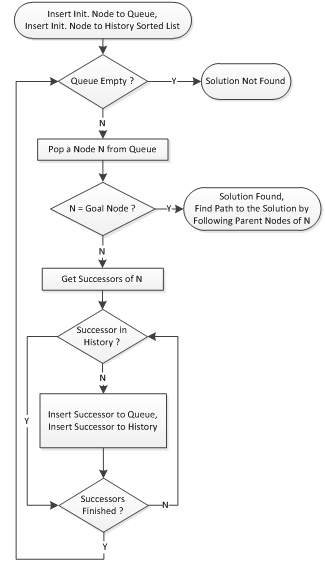
Figure 1: Implemented BFS algorithm
2.1.2. Depth First Search (DFS)
DFS is usually implemented in a recursive manner. I have implemented the recursive version too. However, I did not use it in the final version of my code. The iterative version still can be found in the source code, but the executable program uses non-recursive DFS. It is almost exactly the same as BFS, except for the fact that it uses a stack instead of a queue. In a 3x3 problem, if one is lucky, DFS can find the solution in a few 100 steps. But most of the time it searches almost the entire search space and takes around a minute to solve a 3x3 problem. Due to the fact that 4x4 and larger puzzles have much more states, DFS can be said to fail to find a solution in a reasonable time unless the user is lucky.

Figure 2: Implemented DFS algorithm
2.1.3. Iterative Deepening Depth Limited Depth First Search (IDFS)
I have implemented IDFS in both recursive and non-recursive forms. But only the non-recursive algorithm is used in the final program due to ease of understanding and better ability to track the code.

Figure 3: Implemented DFS algorithm
IDFS has a limit value, and the limit starts from 1. When no solution is found in the first iteration, the limit is increased by 1, and Depth Limited DFS starts again. The limit is increased until a threshold value. In my program that threshold value is larger than 200,000 so that for a 3x3 case a solution is always found. Actually, the limit can never reach that value in a real case since it takes really a lot of time to search the entire search space when the depth limit gets larger. Actually to search a specified depth, IDFS takes longer than BFS since IDFS iteratively searches for all levels. But the good thing with IDFS is that it requires very little memory. Storing an approximate number of nodes equal to the depth limit is enough.
For optimality, in my IDFS, I needed to keep the history but this time the history is slightly modified as seen in figure 3. Now, IDFS always gives an optimal solution. Because if a successor node is found in the history but the successor’s depth is smaller than the one in the history list, it is pushed to the stack and the history is updated.
2.2. Implemented Informed Search Methods
The informed search methods can make a prediction about opening which node will be more beneficial. In this problem the cost of a node can be thought of as its depth since each move costs only 1.
A* is implemented with two heuristic functions. One of them is counting misplaced tiles, the other is counting the total Manhattan distance of all tiles to their goal states. Both heuristics are admissible, i.e., smaller than the actual solving cost. But Manhattan distance gives a closer approximation to the remaining steps than misplaced tiles.
2.2.1. A* with Misplaced Tiles Heuristic (A* Mis)
First, A* is implemented with a total misplaced tiles heuristic. It is similar to the BFS algorithm with the history keeping improvement done in the IDFS algorithm. However, this time, the item with the smallest (Cost + Heuristic) function is popped out of the list. The list is kept in a sorted manner so that accessing the smallest element is much faster than checking all elements in the list. My implemented A* with misplaced tiles heuristic always gives an optimal result. And it is noticeably faster than BFS, DFS, and IDFS. First I will explain A* with Manhattan distance and then give a flowchart of the A* algorithm since it is the same for both heuristic functions, only the calculation of the heuristic changes.
2.2.2. A* with Manhattan Distance Heuristic (A* Man)
A* algorithm with Manhattan distance heuristic gives the most optimal results among all of the implemented algorithms. It stores very little nodes, finds the solution with expanding very little steps and time. With this algorithm, the efficiency of Manhattan distance heuristic for sliding puzzle is proved.
The flowchart of the implemented A* algorithm is as follows:

Figure 4: Implemented A* algorithm
3. Implemented Program
I have implemented my program in C#. As a different specification of C#, we can say that it does not allow the use of pointers with custom classes and pointer arithmetic. However, its predefined structures allow the user to do its work even without pointers. For example, instead of creating back pointers, we can create a parent node, and instead of following back pointers, we can follow parent nodes, i.e., a node stores another node which is its ancestor in its structure. Also, many implementations such as Sorted List are given as default with C#. Furthermore, Microsoft gives probably the best IDE for writing programs, Visual Studio.
The program is divided into many classes for node, puzzle, and different algorithms. If a problem can be represented as a sliding puzzle, my program can solve it.
My implemented program at the start is as follows:

Figure 5: Start screen of main GUI
The user can create his own puzzle, let the PC create a puzzle, load an existing puzzle, or even load a Monte Carlo run immediately. Note that, Monte Carlo data must be generated first. So let us begin with an automatic puzzle generator. It generates a sliding puzzle at the specified true distance by avoiding loops. But it does it in a depth first manner and sometimes solver algorithms can find a shorter path to the solution than the desired step. But at the end, puzzles are examined in their true steps, not in the desired creation step. The automatic puzzle generator can be opened by clicking the “Create Puzzle For Me” button in the main GUI.

Figure 6: Automatic puzzle generator at the start
First, the puzzle size must be chosen, then the desired true step. The puzzle will be generated and displayed automatically. If you do not like the puzzle, just click the “Generate New Puzzle” button. You can repeat until you like the puzzle. For saving a puzzle, click on the “I Like It, Save Puzzle” button. It will let you choose the name and place to save the puzzle. The puzzle is saved as XML. We can open the XML and give any custom state. But the user must ensure the solvability of the puzzle. Otherwise my program also has a manual puzzle generator. The last thing on the Automatic puzzle generator is that, it generates Monte Carlo data consisting of 100 puzzles at the specified step and size. It will not display them but they are just random states. The user can open the Monte Carlo data saved file and examine it. But be sure not to modify it.

Figure 7: A puzzle generated with the Automatic Puzzle Generator
While creating Monte Carlo data, progress is displayed at the top bar of the form. But if you want to cancel the Monte Carlo generation, simply closing the Automatic Puzzle Generator will work and nothing will be saved. You can open many puzzle generators at the same time, since they work independent of the Puzzle Solver.
We can use this to generate a custom puzzle. The Manual Puzzle Generator will do the work. After selecting size, just clicking on the numbered buttons will change the state. The user can save any state that he/she likes. The desired true step will be displayed as -1 for custom puzzles.

Figure 8: Automatic Puzzle Generator generates a 10x10 puzzle at step 100

Figure 9: Manual Puzzle Generator start screen

Figure 10: Manual Puzzle Generator initial state which is the goal state

Figure 11: Manually shuffled puzzle sample
After generating a puzzle, the user can load it to the main GUI. Just clicking on the “Load A Saved Puzzle” button will load the generated puzzle. Once the puzzle is loaded, puzzle specifications will be displayed on the main GUI screen. Initially it will open on “I will solve it option”. This option is not implemented. It would be just for fun and would let the user click on buttons and try to solve the puzzle him/herself. In my program, the puzzle solved data is also saved on the puzzle save file. So if a generated puzzle is solved once, it will display the previously solved statistics. Anyway the user can solve the puzzle as much as he/she wants. When a large puzzle is loaded, the GUI does the resizing automatically. The GUI button placement might be shifted in some computers. But the GUI can easily be resized.
For making the program solve the puzzle, click on the algorithm among the radio buttons and click the “Solve” button. For different algorithms, buttons will be displayed in different colors.

Figure 12: Manually generated puzzle loaded to the main GUI

Figure 13: Main GUI when a large puzzle is loaded
When a puzzle is solved, its solution statistics and solution steps are saved to its created XML file. An example of a saved file is as follows:
="1.0"="utf-8"
<AIMehmutluSlidingPuzzleSaveFile>
<Puzzle.000>
<Size>3</Size>
<State>1,2,3,7,4,5,0,8,6</State>
<DesiredOptimalSolutionStep>-1</DesiredOptimalSolutionStep>
<SolvedAlgorithms>
<BFS>
<Solved>T</Solved>
<SolutionTime>7</SolutionTime>
<NoOfStoredNodes>18</NoOfStoredNodes>
<NoOfNodeExpansion>26</NoOfNodeExpansion>
<SolutionStep>4</SolutionStep>
<SolutionNodes>
<Node0>1,2,3,7,4,5,0,8,6</Node0>
<Node1>1,2,3,0,4,5,7,8,6</Node1>
<Node2>1,2,3,4,0,5,7,8,6</Node2>
<Node3>1,2,3,4,5,0,7,8,6</Node3>
<Node4>1,2,3,4,5,6,7,8,0</Node4>
</SolutionNodes>
</BFS>
<DFS>
<Solved>F</Solved>
<SolutionTime></SolutionTime>
<NoOfStoredNodes></NoOfStoredNodes>
<NoOfNodeExpansion></NoOfNodeExpansion>
<SolutionStep></SolutionStep>
<SolutionNodes>
<Node0>1,2,3,7,4,5,0,8,6</Node0>
</SolutionNodes>
</DFS>
<IDFS>
<Solved>F</Solved>
<SolutionTime></SolutionTime>
<NoOfStoredNodes></NoOfStoredNodes>
<NoOfNodeExpansion></NoOfNodeExpansion>
<SolutionStep></SolutionStep>
<SolutionNodes>
<Node0>1,2,3,7,4,5,0,8,6</Node0>
</SolutionNodes>
</IDFS>
<AStarMisplacedTiles>
<Solved>F</Solved>
<SolutionTime></SolutionTime>
<NoOfStoredNodes></NoOfStoredNodes>
<NoOfNodeExpansion></NoOfNodeExpansion>
<SolutionStep></SolutionStep>
<SolutionNodes>
<Node0>1,2,3,7,4,5,0,8,6</Node0>
</SolutionNodes>
</AStarMisplacedTiles>
<AStarManhattan>
<Solved>F</Solved>
<SolutionTime></SolutionTime>
<NoOfStoredNodes></NoOfStoredNodes>
<NoOfNodeExpansion></NoOfNodeExpansion>
<SolutionStep></SolutionStep>
<SolutionNodes>
<Node0>1,2,3,7,4,5,0,8,6</Node0>
</SolutionNodes>
</AStarManhattan>
</SolvedAlgorithms>
</Puzzle.000>
</AIMehmutluSlidingPuzzleSaveFile>
In the above saved file example, puzzle generation data is at the very top. Also, there are specifically reserved places for different solver algorithms. Once an algorithm solves the puzzle, its statistics is saved to the corresponding spaces. For example, the above data is solved with BFS. BFS statistics are saved to the corresponding spaces and the solution path is also saved as a sequence of states. The above puzzle is just a single puzzle. In Monte Carlo Data, there are 100 puzzles, each named as Puzzle.(Number). For example, Puzzle.024 refers to the 24th puzzle in the Monte Carlo Data.
Therefore, if we load a solved puzzle to the main GUI, it will display the previous solution statistics. Initially the initial node of the puzzle is displayed. If the puzzle is solved, the user can check the solution path by clicking on the buttons having forward and backward arrows on them. Also clicking on the PLAY button will automatically play the previous solution step. Play can be stopped at any time; manually steps can be taken back or forward. Once the solution steps finish, the playing option will display the goal state for two seconds and it will redisplay the initial state.

Figure 14: A manually generated puzzle (step (-1)) is solved with BFS

Figure 15: A manually generated puzzle is solved with DFS

Figure 16: A manually generated puzzle is solved with IDFS

Figure 17: A manually generated puzzle is solved with A* Misplaced Tiles heuristic

Figure 18: A manually generated puzzle is solved with A* Manhattan Distance heuristic
If a very hard puzzle is loaded and you get bored of waiting for the solution, you can simply press the “Stop Solver” button. While working on the GUI, buttons will be enabled or disabled to avoid conflicts in the working order of the program.

Figure 19: The main GUI while resolving a manually generated puzzle with DFS, previous statistics can be seen

Figure 20: Main GUI while solving a Monte Carlo run
Monte Carlo run works in a sequential order. First the 1st puzzle is solved with BFS, DFS, IDFS, A* Mis, and finally with A* Man algorithms, then the second puzzle is solved. It goes for all 100 puzzles. After solving with an algorithm, a solved message is displayed on the GUI. It can be seen on Figure20. But note that BFS, IDFS, A* Mis, and A* Man solve a puzzle at shallow steps much faster than DFS. So their messages are displayed and deleted very quickly. So the message is only noticeable when waiting for an algorithm to solve. For example, in Figure 20, “Puzzle is solved with BFS” is displayed while solving with DFS. And the messages of other algorithms will be skipped very quickly since they will solve very quickly. It is not a bug.
A* Man is a pretty good algorithm. It can solve puzzles very quickly unless the puzzle is extremely shuffled. In Figure 26, the capability of A* Man is displayed. A 10x10 puzzle at 58 true steps is solved in 7 seconds.

Figure 21: Capability test of A* Manhattan Distance heuristic
4. Implemented Complementary Programs
4.1. Data Converter in C#
In order to plot performance plots on MATLAB, solution statistics data need to be extracted with MATLAB. In order to simplify work in MATLAB, I wrote a small standalone program for converting XML solved Monte Carlo data to simpler text format. I wrote different variations of the same conversion program for algorithm comparison and size comparison. Size comparison with A* was not very explanatory. I will give details in the next section about it, so I also performed size comparison with BFS.

Figure 22: XML to text converter and data decoder for algorithm comparison Monte Carlo data

Figure 23: XML to text converter and data decoder for size comparison Monte Carlo data with A* Man algorithm

Figure 24: XML to text converter and data decoder for size comparison Monte Carlo data with BFS algorithm
After solving various 100 puzzle Monte Carlo data, the XML files are converted to text with the above programs. Write the future name of the decoded data file on to a text file on the mini program, then click on the only available button on the GUI. It will ask you to locate the solved Monte Carlo data in an XML file. Once the XML file is given, it will generate the decoded text file in the directory in which the executable file resides. Once the text files are ready they will be fed to MATLAB functions that will be plotting the data.
4.2. Data Plotter in MATLAB
In order to have nice plots, I wrote MATLAB functions that will take many Monte Carlo run decoded text data and extract the information. Functions will only ask for directory containing Monte Carlo runs. Finally, it will give the plots. For different data runs, small parameter changes in the MATLAB functions are necessary. MATLAB .m files containing MATLAB functions are also given in the folder submitted with this report. Since MATLAB functions are quite lengthy, code will not be presented in this written report.
5. Results
5.1. Algorithms' Analysis
For algorithm comparison, 100 3x3 puzzle lots are created at desired true steps 5, 10, 15, 20, and 25. A total of 500 puzzles are solved with five different algorithms, i.e., a 2500 solution is used as the database. All created puzzles are not at the desired steps since they are created in a depth first fashion as explained in the “Take Home Definition” sheet. But they are delicately separated into true step arrays and data is examined for true steps. The resulting data has steps varying from 4 to 25 (4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25). All data is plotted on the MATLAB graphs in blue dots. But when the number of samples at true step exceeds the threshold value which was set to 20, the ensemble at the same true step is considered as a thrust worthy ensemble and averaged and marked with red circles on the plots.
The rest of the page is intentionally left blank so the result of an algorithm can be seen in 1 page.
The BFS algorithm gives exponential results for everything. Notice the saturation like phenomenon in the stored node data. The reason is the fact that I use history in the BFS algorithm. When the history covers almost the entire search space, only a small portion of all expanded nodes can be stored because all others are already in the history, i.e., they are already visited at a lower level.

Figure 25: BFS time performance at 3x3 puzzle size

Figure 26: BFS node expansion at 3x3 puzzle size

Figure 27: BFS node storage at 3x3 puzzle size
For DFS, notice that the step size does not matter so much. DFS searches the entire search space or it finds the goal very quickly. But when the data is averaged, the DFS performance is almost the same. This result is just as expected. In the comparative figures, DFS seems to be inferior to others but that is mainly because of the fact that we usually apply data at very low step solution. If we would give puzzles at higher step, the BFS solution time would keep increasing but the DFS average solution time would still be almost half the time required for searching the entire search space. The same also applies for other attributes.

Figure 28: DFS time performance at 3x3 puzzle size

Figure 29: DFS node expansion at 3x3 puzzle size

Figure 30: DFS node storage at 3x3 puzzle size
IDFS find the solution in a longer time when compared to BFS. In IDFS, node expansion rate and solution times are both exponential and worse than BFS. However, when it comes to stored nodes, IDFS is extremely superior. It only stores nodes around the number of depth the solution is found. So, with true step puzzles, memory usage is almost linear with steps. IDFS requires more CPU power than BFS but you can save from RAM.

Figure 31: IDFS time performance at 3x3 puzzle size

Figure 32: IDFS expanded nodes at 3x3 puzzle size

Figure 33: IDFS stored nodes at 3x3 puzzle size
Informed searches perform much better than uninformed searches on overall performance. Although IDFS stores less number of nodes, its solution time can never compete with the A* solution time. Statistics are still exponential for A*. But the level of stored nodes and expanded nodes is much better than BFS and DFS. We can easily conclude that informed search is much better than uninformed ones.

Figure 34: A* Mis time performance at 3x3 puzzle size

Figure 35: A* Mis expanded nodes at 3x3 puzzle size

Figure 36: A* Mis stored nodes at 3x3 puzzle size
In the A* Manhattan distance data we can conclude that a better heuristic is the one that gives closer values to the actual optimal solution cost. The solution time in the A* Manhattan distance case does not give much information. I noticed some strange periodic increase in the data. That can be due to the Operating System’s thread management. But the expanded nodes and stored nodes data give the exponential trend correctly. A* Man proves its effectiveness in the sliding puzzle solution.

Figure 37: A* Man time performance at 3x3 puzzle size

Figure 38: A* Man expanded nodes at 3x3 puzzle size

Figure 39: A* Man stored nodes at 3x3 puzzle size
5.2. Puzzle Size Analysis
For observing puzzle size effect on the same algorithm, various sized (3x3, 4x4 … 10x10) 100 puzzle lots are created at a specific true step. They are solved with an algorithm and statistics are plotted. All data is plotted on the MATLAB graphs in blue dots. But when the number of samples at true step and specified size remain above the threshold value which was set to 20, the ensemble at the same true step is considered as a thrust worthy ensemble and averaged and marked with red circles on the plots.
The generated puzzled was not always at the desired step. So I just discarded the data which was not at the desired step. So the ensemble size at a specific step and size is reduced from 100 to smaller numbers. The drop was drastic in small puzzle sizes. But note that reliable data is marked with red.
First I experimented with A* Man at 20 steps. I could not conclude meaningful results and repeated the test with A* Man at 35 steps. But still could not come up with reasonable explanation. Finally, I repeated the test with 10 step puzzles and the BFS algorithm. I will include all of my experiments and my explanations.
The rest of the page is intentionally left blank so that puzzles corresponding to the same step and solved with the same algorithm can be shown in one page.
The A* Man algorithm did not give very meaningful results for puzzle size effect observation. I could not catch any data trend except slightly high numbers for puzzle size 4. It seems that more shuffled puzzles are harder to solve for A* Man. Even though the search space is smaller for size 4 puzzles, A* worked harder to get to the result when compared to the larger puzzles at the same true step.

Figure 40: A* Man stored nodes vs. puzzle size at 20 step

Figure 41: A* Man time performance vs. puzzle size at 20 step

Figure 42: A* Man expanded node vs. puzzle size at 20 step
In order to confirm my results with A*, I performed the same test at 35 step Monte Carlo Runs. A* does not seem to be affected by the puzzle size a lot.

Figure 43: A* Man time performance vs. puzzle size at 35 step

Figure 44: A* Man expanded node vs. puzzle size at 35 step

Figure 45: A* Man stored node vs. puzzle size at 35 step
Then I performed the same test with BFS. I noticed linear-exponential like trends for puzzle solving statistics. I can conclude that this is due to the fact that effective exponential is increasing. What I mean is that: when puzzle size is 3 and blank at the corner (4 times), the state has two successors; when blank is at the edge (4 times), the state has 3 successors; when blank is at the middle, state has 4 successors (1 time). The effective exponential factor is approximately 2.6. If we consider that one of the successors is causing a loop, my algorithms will not store it effective exponential factor decreases to 1.6. But, when puzzle size is 4 and blank at the corner (4 times), the state has 2 successors; when blank is at the edge (8 times), the state has 3 successors; when blank is at the middle, the state has 4 successors (4 times). The effective exponential factor is 3. If we consider that one of the successors is causing a loop, my algorithms will not store it if effective exponential factor decreases to 2. So I can conclude that puzzle size increase increases the effective exponential factor hence more stored nodes, more expanded nodes, and longer solution time is plausible for larger puzzles.

Figure 46: BFS time performance vs. puzzle size at 10 step

Figure 47: BFS expanded nodes vs. puzzle size at 10 step

Figure 48: BFS stored nodes vs. puzzle size at 10 step
6. Conclusion
I have implemented five different algorithms on the sliding puzzle problem. The experience I gained from the implementation of this take home examination is very valuable. Now I am well aware of the real life behavior of these algorithms.
All algorithms are able to find solutions. Furthermore, all algorithms except DFS can find the shortest (optimal) solution in my implementation. My puzzle representation with history nodes increased the performance of algorithms significantly and made the DFS solution possible for this project.
Exponential characteristics of BFS were trivial and they are observed very clearly on this project.
Also, the specification of DFS to find the solution at the average of searching half of the search-space was very obvious. If we could give problems at higher true steps, DFS would find the solution quicker than BFS, since BFS would be searching for the entire search space and DFS would be searching for half of it on the average.
The importance of IDFS was not very clear for me in the class but I noticed that IDFS solves the problem with minimal storage requirements at the expense of CPU power and time.
As expected, informed search algorithms performed much better on overall solution performance. Having a better heuristic also increased the performance very clearly.
The program I obtained at the end well satisfied me. It has been the largest piece of code that I have written so far and its performance really is satisfying.
7. Acknowledgement
I would like to thank Orkun Ögücü for his support in MATLAB data plotting and Serhat Varolgünes for his support in multi-threading in C#.
8. References
[1] Artificial Intelligence: A Modern Approach (3rd Edition); Stuart Russell, Peter Norvig; Pearson education series in artificial intelligence.
9. Appendix
The decoded algorithm comparison Monte Carlo text data that is obtained for easier plotting in MATLAB is in the following format. “P” for puzzle; “000”, “001” stands for puzzle number; “B”, “D”, “I”, “A”, “M” stand for BFS, DFS, IDFS, A*Mis, A*Man, respectively. “ST” stands for stored node; “SS” stands for solution step; “EN” expanded nodes; “SN” stored nodes. The numbers after initials give the proper number for that value. The Monte Carlo text decoded data was actually for 100 puzzles but only 3 puzzle statistics are given in here.
P 000 B ST 31 SS 5 EN 43 SN 30
P 000 D ST 39718 SS 129 EN 181323 SN 59444
P 000 I ST 0 SS 5 EN 110 SN 7
P 000 A ST 0 SS 5 EN 7 SN 9
P 000 M ST 0 SS 5 EN 6 SN 7
P 001 B ST 0 SS 5 EN 50 SN 42
P 001 D ST 36442 SS 213 EN 181248 SN 59439
P 001 I ST 0 SS 5 EN 92 SN 7
P 001 A ST 0 SS 5 EN 6 SN 7
P 001 M ST 0 SS 5 EN 6 SN 7
P 002 B ST 15 SS 5 EN 58 SN 41
P 002 D ST 0 SS 13 EN 14 SN 12
P 002 I ST 0 SS 5 EN 77 SN 6
P 002 A ST 0 SS 5 EN 6 SN 7
P 002 M ST 0 SS 5 EN 6 SN 7
P 003 B ST 0 SS 5 EN 49 SN 42
P 003 D ST 69888 SS 215 EN 181247 SN 59439
P 003 I ST 0 SS 5 EN 94 SN 7
P 003 A ST 0 SS 5 EN 6 SN 7
P 003 M ST 0 SS 5 EN 6 SN 7
The size comparison data has only one algorithm. But it also has size info denoted by “S” at the very end. The following decoded Monte Carlo Data belongs to size 4 puzzles. Only 6 of them are displayed here but a file contains data for 100 puzzles.
P 000 M ST 31 SS 31 EN 771 SN 801 S 4
P 001 M ST 0 SS 25 EN 274 SN 274 S 4
P 002 M ST 15 SS 25 EN 319 SN 323 S 4
P 003 M ST 1030 SS 29 EN 10124 SN 10256 S 4
P 004 M ST 172 SS 29 EN 2996 SN 3193 S 4
P 005 M ST 0 SS 25 EN 317 SN 321 S 4
All original decoded data that are used for plotting in MATLAB can be found in the MATLAB folder presented with this project.
