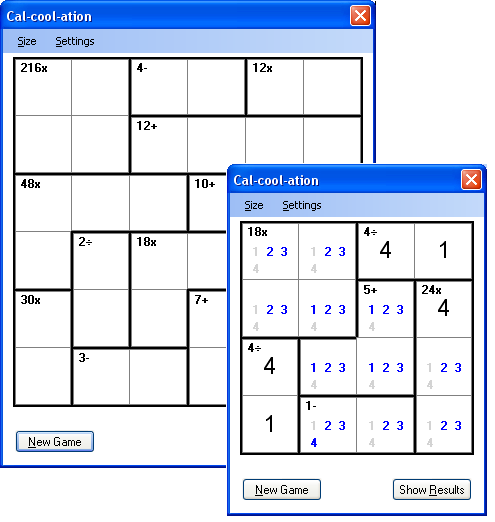
Introduction
"Calcoolation" is a puzzle game that at first looks like the popular Sudoku. Just like in Sudoku, you have an N x N matrix, where the digits 1 through N must be placed in each column and in each row without repetition. The difference lies in the fact that there are blocks of cells, named "cages", where specific operations involving the numbers in the cells must satisfy the specific result displayed in the cage.
Background
This game was invented by the Japanese teacher Tetsuya Miyamoto in 2004, under the name "KenKen" (Ken is the Japanese word for "cleverness"), although I only became aware of it in the beginning of this year. I got very impressed ("puzzled") by it, and then decided to develop the game in C#.
The most challenging part was to discover the correct strategy to pick the random numbers without repetitions in columns and rows. I decided to use the "Naked Pairs/Naked Triplets" strategy, which I borrowed from some sites dedicated to Sudoku solving. I'll discuss Naked Pairs later on in this article.
After picking all the numbers, I still had to randomly create the "cages". Cages are sets of contiguous cells in the board. I did this by randomly selecting pairs of cells in random directions, beginning from the top/left corner. Thus, initially the cages had two cells, but when a random cage cell superposes another cage cell, those cages are merged, so we could have 3-pieces and 4-pieces cages.
The Code
The code is divided into two layers: Core and WinUI. In the WinUI layer, we have the Windows Forms presentation logic. It's a very simple user interface, intended to make the player life easier. The important note here is that I created a user control ("CellBox") to hold the cell data, functionality, and events. In Windows Forms, user controls are useful tools for separation of concerns on the UI side.
The Core layer does most of the hard work. It's composed of classes that represent the three main entities in the game: the Board, the Cage, and the Cell. There can be only one Board in the game (that's why I decided to use the Singleton pattern). The default Board has the predefined dimension 4x4 (which can be changed later by the user). Each position in the board is held by a cell (that is, cell count = size²). Inside the board, the cells are also arranged in pieces called "Cages" (much like a traditional puzzle).
The pieces of code that I think worth mentioning are those related to random number picking, random cage formation, and game complete testing.
Random Number Picking
For random number picking, see the GenerateNumbers() method:
private void GenerateNumbers()
{
ResetBoard();
Random rnd = new Random();
string number = "0";
int minSize = size;
int maxSize = 0;
bool someSolved = true;
while (someSolved)
{
someSolved = false;
if (!someSolved)
{
}
if (!someSolved)
{
}
for (int row = 0; row < size; row++)
{
}
for (int row = 0; row < size; row++)
{
}
if (!someSolved)
{
}
}
}
Notice that, according to the code above, the naked pairs are resolved in the beginning. Then, the naked triplets, and then the cells with a unique solution, and then the random selection. This is done so to avoid backtracking.
As a result, we now have a valid board, ready to be used:

Random Cage Formation
The next important step is to randomly create the cages, and here is the GenerateCages method:
private void GenerateCages()
{
cages = new List<Cage>();
bool success = false;
int orientation = 0;
int c2 = 0;
int r2 = 0;
Random rnd = new Random();
for (int r = 0; r < size; r++)
{
for (int c = 0; c < size; c++)
{
if (matrix[c, r].Cage == null)
{
success = false;
while (!success)
{
orientation = rnd.Next(1, 5);
switch (orientation)
{
case 1:
c2 = c - 1;
r2 = r;
break;
case 2:
c2 = c + 1;
r2 = r;
break;
case 3:
c2 = c;
r2 = r - 1;
break;
case 4:
c2 = c;
r2 = r + 1;
break;
}
if (c2 >= 0 && c2 < size && r2 >= 0 && r2 < size)
{
Cage cage = matrix[c2, r2].Cage;
if (cage == null)
{
cage = new Cage();
cage.CellList.Add(matrix[c2, r2]);
matrix[c2, r2].Cage = cage;
}
else
{
if (cage.CellList.Count > 3 && (c != size - 1 || r != size - 1))
{
continue;
}
}
cage.CellList.Add(matrix[c, r]);
matrix[c, r].Cage = cage;
cages.Add(cage);
success = true;
}
}
}
}
}
Starting from the {0,0} position on the board, and moving to the right and down directions, this function places pieces of two cells in random directions, and tests whether there is a conflict with an existent cage. In this case, the cages are merged; otherwise, a new cage is created:

After that, the PickOperation() method chooses a possible random operation (picked between +, -, x, and ÷) using the numbers inside the cage.
public void PickOperation(Cage cage)
{
bool success = false;
while (!success)
{
if (currentOperation == 5)
currentOperation = 1;
switch (currentOperation)
{
case 1:
cage.Operation = Operations.Plus;
int sum = 0;
foreach (Cell cell in cage.CellList)
{
sum += Convert.ToInt32(cell.CellValue);
}
cage.Result = sum;
success = true;
break;
case 2:
cage.Operation = Operations.Minus;
if (cage.CellList.Count == 2)
{
int sub = Convert.ToInt32(cage.CellList[0].CellValue) -
Convert.ToInt32(cage.CellList[1].CellValue);
if (sub > 0)
{
cage.Result = sub;
success = true;
}
else
{
sub = Convert.ToInt32(cage.CellList[1].CellValue) -
Convert.ToInt32(cage.CellList[0].CellValue);
if (sub > 0)
{
cage.Result = sub;
success = true;
}
}
}
break;
case 3:
cage.Operation = Operations.Multiply;
int mult = 1;
foreach (Cell cell in cage.CellList)
{
mult *= Convert.ToInt32(cell.CellValue);
}
cage.Result = mult;
success = true;
break;
case 4:
cage.Operation = Operations.Divide;
if (cage.CellList.Count == 2)
{
int quo = Convert.ToInt32(cage.CellList[0].CellValue) /
Convert.ToInt32(cage.CellList[1].CellValue);
int rem = Convert.ToInt32(cage.CellList[0].CellValue) - quo *
Convert.ToInt32(cage.CellList[1].CellValue);
if (rem == 0)
{
cage.Result = quo;
success = true;
}
else
{
quo = Convert.ToInt32(cage.CellList[1].CellValue) /
Convert.ToInt32(cage.CellList[0].CellValue);
rem = Convert.ToInt32(cage.CellList[1].CellValue) - quo *
Convert.ToInt32(cage.CellList[0].CellValue);
if (rem == 0)
{
cage.Result = quo;
success = true;
}
}
}
break;
}
currentOperation++;
}
}
Getting Smarter: Playing With Candidates
I must confess that I found this game difficult for me. I can face a 3 x 3 board, but from 4 x 4 on, things get more complicated. If I had this game on paper, I would probably take notes about which numbers can or can't be placed in cells. Then I discovered the correct digit for a certain cell, I'd pick up my pencil to strike through that digit in the other cells in the same row and the same column. Then I had this weird idea: what if I allowed users to take notes directly in the application? And here it is, this new feature through the menu "Settings -> Show Candidates", where you can turn on/off the candidate digits:

Notice that when you play with candidates, the interface changes a little bit:

The Naked Pairs
Before getting a random number for a cell, you should always look for "naked pairs". Naked pairs mean that in some row or column, there are two cells with two possible values. In the figure below, we can spot these naked pairs, with only two possible values [3,4]:

The reason for spotting naked pairs is simple: since these two cells can hold only these two digits, no other cells in that row will have "3" or "4". Thus we can remove them from the possible digits:

Points of Interest
I think the harder part for me was to discover how to randomly arrange the numbers in a valid N x N board (that is, without repeating digits in rows and columns). After some research, I found the naked pairs / naked triplets technique I mentioned before. Of course, there are many more techniques I could have used, so if you are interested in them, not only as a developer, but also as a player, here it goes:
History
- 2009-07-26: First post
- 2009-07-29: New feature: "Show Candidates"
- 2009-07-30: New version for Visual Studio 2005
