Create a Voronoi diagram 2 of 3

• Download WPF_VORONOI_TEST-Part2.zip - 86.1 KB

Introduction   

The code used in this article is based on my previous article Create a Voronoi diagram 1 of 2 (Seems I was a little optimistic as I called it 1 of 2 instead of 1 in 3). If you have any questions related to the basic functions you should check the article first as Im going to assume that you know the information described there. 

Voronoi diagrams based on Fortune's algorithm is quite complicated to implement, and for that reason I will give many different test projects so you can follow the implementation step by step.

Background   

We want to construckt a Voronoi diagram, and as explained in the previous article, there are two events that make up the changes in a Voronoi diagram based on Fortune's sweep line method, namely:

1. Site event, a new point apperes on the sweep line
2. Circle event, this could happened before the sweep line finds the next point, and it is the only time where an arc would disappear and would never become visible again.  

As we move along the sweep line we quicly realize that we need to store some information as we go along, and we need to find out were the lines sould be cut.    

The Binary search tree   

Assume that we have all the point sorted as we begin with the sweepline decent. We hit the first point, and we know that this point would not form a line by itself, and that it cant form a circle event, as there is not enough points to do that yet. 

We then hit point nr 2, and we know that point 1 and point 2 will form a line, as we have sorted the points. This new line would also be the first child in the Voronoi diagram.

But now as we decend it becomes more difficult, as we dont know if its a circle event or a new line event. So we have two possibilities: 

1. It's a circle event, and the existing line which contain two of the tree points in the circle. These tree points form a circle that does not have any other points inside it. This means that our first line would have at least two new children. One to the right and one to the left.
2. It is a new cite event, and the new line would have to be added as an additional child to the Voronoi diagram. But were sould it be added, and the answer is that it should be added were it is either all to the left or all to the right.  

What shoud we do in a situation that have a circle event, with the circle center lies beound our box? Well this is a significant event as we would have to cut our previous calculated line. We typically get this in a situation seen below, were our two first points create a line, that would have to be cut outside our bondary. We can, of cource refuse, to calculate any points outside the boundary, but that would give us problems concerning two points that form a line not visible by our boundary box, and divides thje line before we can see the first line in the diagram.

To keep contol over all these events we need a place to store all the information about the calculated lines and Voronoi verzities as we go along. The binary tree is the perfect candidate for this. However all this talk about parabolic arcs that dissapear may be a bit misleading, becouse it is not the points that dissapear, it is simply the possiblility that the two previous points can form a new line in the Voronoi diagram. Take a look at the illustration below: 

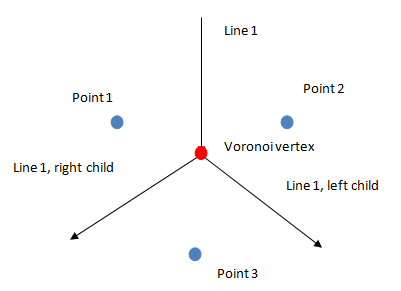
The Voronoi vertex simply says, well, point 1 and point 2 together wont effect the Voronoi diagram toghether any more. But Point 1 and Point 3 will, as will Point 2 and Point 3. This is important to understand. It is not the original points themselvs that is affected, but the relationship between the two of them. (The funny thing is that it reminds me of a divorce in many aspects, and the two old points is forced by the events in the sweep line to find a new partner. ) 

There is one more problem with doing this programatically. That is Line one, will have its endpoint cut by the Voronoi vertex, and the two new lines will both have a startpoint in the Voronoi vertex. But on which side sould I set the endpoint? If you see the picture below, it contains tree points. The old line is simple to cut as we know that the enpoint is the Voronoi vertex, but the two new lines are more problematic to cut, we know were our new lines starts, but which one of the two points is the correct one to keep? The problem is illustrated below, and please remember that this would have to be true for all the circle events:  

The simplast way of selectiong the point that would be its end point would be to determine if a point would be on the same side relative to the old line, this is based on the cross product of two vectors and an explaination could be found here. 

There is also the possibility that two separate lines would form the tree points in a circle. That situation is simpler to calculate, as both of the lines will have a new endpoint, and the line would continue with two of the tree points. This would usually happen when you close a Voronoi cell.

We also understand that points that lie on a straight line, can't form a circle, and we should check for circle events were this is not the case. If you look at the secound example below we can clearly see that the tree points cant form any circle, and all of the points would have to be parants of the first empty Voronoi line. (This would also happen if the middle point is higher that the two points on each side, as the circle event has not happened yet.)

 

So how can we use all this stored information of newly created lines? We assume that our lines would form some kind of fractal tree like the illustration from Wikipedia:

The major advantage of binary search trees over other data structures is that the related sorting algorithms and search algorithms such as in-order traversal can be very efficient. This is how we get the O(log n) complexety in Fortunes algorithm from.  

To see how it is useful take a look at the picture below:

We now realize that our beach line could be extrapolated from the binary tree. We also notice that we can find all the circle events from the binary tree, as we could simply check the beach line points to the left and right of the center point to create a new circle. It is vital that you understand that any  circle event would always be found like this, as this would be used leater.

We assume that we would have to keep track of our center points that form the beach line, but as a circle events is the only event that could remove any points, we realize that it is only nessesary to store the points we need to check with the circle event, and we will automatically get the beach line points. And if we use the information stored in the binary tree as the information needed on which potential circle events would appear.   

Storing Voronoi lines for all the Voronoi points

We need a class for all the original points that would form the closed polygon for any of the center points. This class would also have to include some check's for all the termination of lines. The ultimate question is how much information do we need to store? 

We can easily calculate the corresponding line function using the information on a line generated by two points. The class I created for storing the points now looks like this:

 Public Class VoronoiLine

    Sub New()

    End Sub

    Private _VoronoiParent As VoronoiLine
    Public Property VoronoiParent() As VoronoiLine
        Get
            Return _VoronoiParent
        End Get
        Set(ByVal value As VoronoiLine)
            _VoronoiParent = value
        End Set
    End Property

    Private _VoronoiChildren As New List(Of VoronoiLine)
    Public Property VoronoiChildren() As List(Of VoronoiLine)
        Get
            Return _VoronoiChildren
        End Get
        Set(ByVal value As List(Of VoronoiLine))
            _VoronoiChildren = value
        End Set
    End Property

    'A check to see if one of the points is the same as the creation point
    Public Function Contains(ByVal P As Point) As Boolean
        If CreationPointLeft = P Or CreationPointRight = P Then
            Return True
        Else
            Return False
        End If
    End Function

    ''' <summary>
    ''' Finds which side of a line the point is
    ''' </summary>
    ''' <param name="PointToBeEvaluated">Evaluation point</param>
    ''' <returns>-1 for a point to the right, 0 for a point on the line, +1 for a point to the left</returns>
    ''' <remarks></remarks>
    Public Function WhichSide(ByVal PointToBeEvaluated As Point) As Integer

        Dim ReturnvalueEquation As Double
        ReturnvalueEquation = ((PointToBeEvaluated.Y - Me.StartPoint.Y) _
                               * (Me.EndPoint.X - Me.StartPoint.X)) - ((Me.EndPoint.Y - Me.StartPoint.Y) _
                               * (PointToBeEvaluated.X - Me.StartPoint.X))

        If ReturnvalueEquation > 0 Then
            Return -1
        ElseIf ReturnvalueEquation = 0 Then
            Return 0
        Else
            Return 1
        End If
    End Function

    Private _CreationPointRight As New Point
    Public Property CreationPointRight() As Point
        Get
            Return _CreationPointRight
        End Get
        Set(ByVal value As Point)
            _CreationPointRight = value
        End Set
    End Property

    Private _StartPointCreatedByCircle As Boolean = False
    Public Property StartPointCreatedByCircle() As Boolean
        Get
            Return _StartPointCreatedByCircle
        End Get
        Set(ByVal value As Boolean)
            _StartPointCreatedByCircle = value
        End Set
    End Property


    Private _EndPointCreatedByCircle As Boolean = False
    Public Property EndPointCreatedByCircle() As Boolean
        Get
            Return _EndPointCreatedByCircle
        End Get
        Set(ByVal value As Boolean)
            _EndPointCreatedByCircle = value
        End Set
    End Property

    Private _CreationPointLeft As New Point
    Public Property CreationPointLeft() As Point
        Get
            Return _CreationPointLeft
        End Get
        Set(ByVal value As Point)
            _CreationPointLeft = value
        End Set
    End Property

    'Use this if you want to cut the lines afterword
    Sub New(ByVal p1 As Point, ByVal p2 As Point)

        'In this class it is irrelevant witch point is the startpoint
        'and witch is the endpoint, as they are only used to calculate
        'the line equation coefficients first.
        StartPoint = p1
        EndPoint = p2
    End Sub

    'Use this if you want to cut the lines at creation
    Sub New(ByVal p1 As Point, ByVal p2 As Point, ByVal b As Boundary)

        'In this class it is irrelevant witch point is the startpoint
        'and witch is the endpoint, as they are only used to calculate
        'the line equation coefficients. However they cant be equal.
        StartPoint = p1
        EndPoint = p2

        CutLinesByBoundaries(b)
    End Sub

    Private _StartPoint As New Point
    Public Property StartPoint() As Point
        Get
            Return _StartPoint
        End Get
        Set(ByVal value As Point)
            _StartPoint = value
        End Set
    End Property

    Private _EndPoint As New Point
    Public Property EndPoint() As Point
        Get
            Return _EndPoint
        End Get
        Set(ByVal value As Point)
            _EndPoint = value
        End Set
    End Property

    'It is important to notice that another line event would never cut an existing line!
    'A line can only be cut if one of these two events below occurs!

    'All the calculated lines must in any event be cut by the boundaries
    'This is mearly a test function and has to be changed later on.
    Public Function CutLinesByBoundaries(ByVal Box As Boundary) As Polyline
        ' We first calculate the equation coefficients
        CalculateLineEquation(StartPoint, EndPoint)

        Dim TempTopY, TempTopX, TempBottomY, TempBottomX As Double

        TempTopY = Box.TopLeft.X * A + B
        TempTopX = (Box.TopLeft.Y - B) / A

        TempBottomY = Box.BottomRight.X * A + B
        TempBottomX = (Box.BottomRight.Y - B) / A

        'Deals with startpoint
        If Not StartPointCreatedByCircle Then
            If TempTopX > Box.TopLeft.X Then
                If TempTopX < Box.BottomRight.X Then
                    StartPoint = New Point(TempTopX, Box.TopLeft.Y)
                Else

                    StartPoint = New Point(Box.BottomRight.X, TempBottomY)
                End If
            Else
                StartPoint = New Point(Box.TopLeft.X, TempTopY)
            End If
        End If

        'Deals with endpoint
        If Not EndPointCreatedByCircle Then
            If TempBottomX > Box.TopLeft.X Then
                If TempBottomX < Box.BottomRight.X Then
                    EndPoint = New Point(TempBottomX, Box.BottomRight.Y)
                Else
                    EndPoint = New Point(Box.BottomRight.X, TempBottomY)
                End If
            Else
                TempBottomY = Box.TopLeft.X * A + B
                EndPoint = New Point(Box.TopLeft.X, TempBottomY)
            End If
        End If

        Dim d As New Polyline
        d.Points.Add(StartPoint)
        d.Points.Add(EndPoint)
        d.ToolTip = Math.Round(StartPoint.X, 0) & " and  " & Math.Round(StartPoint.Y, 0) & "; " & Math.Round(EndPoint.X, 0) & " and  " & Math.Round(EndPoint.Y, 0)
        d.Stroke = Brushes.Black
        d.StrokeThickness = 2
        Return d
    End Function

    'All the lines in the center of the Voronoi map would be cut by at least one or two circle events
    Public Function GetLine() As Polyline
        Dim d As New Polyline
        d.Points.Add(StartPoint)
        d.Points.Add(EndPoint)
        d.Stroke = Brushes.Black
        d.StrokeThickness = 2
        Return d
    End Function
    'We will store up to two points in the private collection
    Private CircleEvents As New List(Of Point)

    Private LineIsCreatedFromVertexEvent As Boolean = False

    Public Sub CircleEventAppear(ByVal CircleCenter As Circle)
        CircleEvents.Add(CircleCenter.CenterPoint)
        If CreationPointLeft = Nothing Then
            LineIsCreatedFromVertexEvent = True
        End If
    End Sub

    Public Sub CutLineOnCircleEvents()

        'If we at the end end up with just one circle event we would have to assume that
        'the line go's from the one Voronoi vertex (circle point) to one of the boundaries

        If CircleEvents.Count = 0 Then
            'This could happen if we for instance design a Voronoi diagram with just two points
            Exit Sub
        End If

        If CircleEvents.Count = 1 Then
            'The circle cuts the line in half, the question is witch half sould you cut?
            If LineIsCreatedFromVertexEvent Then
                ' The Vertex is below either one or both line creation points meaning that it is
                ' Remove the line that goes from the higest Y point
                _StartPoint = CircleEvents(0)
            Else
                _EndPoint = CircleEvents(0)
            End If
        Else
            'The maximum circle event for a single line is two
            If CircleEvents(0).Y > CircleEvents(1).Y Then
                _StartPoint = CircleEvents(0)
                _EndPoint = CircleEvents(1)
            Else
                _StartPoint = CircleEvents(1)
                _EndPoint = CircleEvents(0)
            End If
        End If

        'To determine witch of the two boundary points we would have to remove, we can do that by checking the creation point
        'and the circle point. If the circle point is below the CreationPoint, The line below have to go, and if the circle
        'point is above the CreationPoint the line above have to be cut. Remember that this is only valid if just one circle
        'event is present when the diagram is completed!

    End Sub

    'Line equation coefficients, only used internally in this class
    ' y = Ax + B
    Dim A, B As Double

    Private Sub CalculateLineEquation(ByVal p1 As Point, ByVal p2 As Point)
        'Calculate and store the A and B coefficients from the equation here
        'http://en.wikipedia.org/wiki/Line_equation#Two-point_form

        Dim slope As Double
        slope = (p2.Y - p1.Y) / (p2.X - p1.X)
        A = (slope)
        B = (-slope * p1.X + p1.Y)
    End Sub

    ''' <summary>
    ''' Calculates the line between two Parabolic intersections
    ''' </summary>
    ''' <param name="Point1">A point in the Voronoi diagram</param>
    ''' <param name="point2">A Point in the Voronoi diagram (different from point 1)</param>
    ''' <param name="ys">The position of the sweep line</param>
    ''' <remarks>It would give wrong values if the two points have the same or close to the same Y coordinate, as the double has limited significant storage</remarks>
    Public Sub ParabolicCut(ByVal Point1 As Point, ByVal point2 As Point, ys As Double) 'As VoronoiLine

        'Stores the values in double format, as I didnt bother to rewrite Benjamin Dittes quadratic equation.
        Dim x1, y1, x2, y2 As Double

        'Inizialize Point 1
        x1 = Point1.X
        y1 = Point1.Y

        'Inizialize Point 2
        x2 = point2.X
        y2 = point2.Y



        'Sweep line, added 500 to make sure the two calculated points are well of the boundaries
        ys = ys + 500

        'Setting ut calculation of the quadratic equation
        Dim a1 As Double = 1 / (2 * (y1 - ys))
        Dim a2 As Double = 1 / (2 * (y2 - ys))

        'The two resulting values of x from the quadratic equation
        Dim xs1 As Double = 0.5 / (2 * a1 - 2 * a2) * (4 * a1 * x1 - 4 * a2 * x2 + 2 * Math.Sqrt(-8 * a1 * x1 * a2 * x2 - 2 * a1 * y1 + 2 * a1 * y2 + 4 * a1 * a2 * x2 * x2 + 2 * a2 * y1 + 4 * a2 * a1 * x1 * x1 - 2 * a2 * y2))
        Dim xs2 As Double = 0.5 / (2 * a1 - 2 * a2) * (4 * a1 * x1 - 4 * a2 * x2 - 2 * Math.Sqrt(-8 * a1 * x1 * a2 * x2 - 2 * a1 * y1 + 2 * a1 * y2 + 4 * a1 * a2 * x2 * x2 + 2 * a2 * y1 + 4 * a2 * a1 * x1 * x1 - 2 * a2 * y2))

        'Generate two points to store the two intersection points
        Dim p1, p2 As New Point
        p1.X = xs1
        p2.X = xs2
        p1.Y = 0
        p2.Y = 0

        'Find the resulting Y values calculated from the quadratic equation
        ' (It dosent matter that the Y is 0 as the function Intersection2 only uses the X value for computation)
        p1.Y = Intersection2(p1, Point1, ys)
        p2.Y = Intersection2(p2, Point1, ys)

        'Sort first and then add the two calculated poitns
        If p1.Y > p2.Y Then
            Me.StartPoint = (p1)
            Me.EndPoint = (p2)
        ElseIf p1.Y = p2.Y Then
            ' if they are the same save them in the order of the X values
            If p1.X < p2.X Then
                Me.StartPoint = (p1)
                Me.EndPoint = (p2)
            Else
                Me.StartPoint = (p2)
                Me.EndPoint = (p1)
            End If
        Else
            Me.StartPoint = (p2)
            Me.EndPoint = (p1)
        End If

        If WhichSide(Point1) >= 0 Then
            CreationPointRight = Point1
            CreationPointLeft = point2
        Else
            CreationPointRight = point2
            CreationPointLeft = Point1
        End If



    End Sub

    ''' <summary>
    ''' Returns the y value construcked by the event from the newpoint and the contructed arc of the oldpoint
    ''' </summary>
    ''' <param name="NewPoint">This is the point on the sweep line</param>
    ''' <param name="OldPoint">This is one point above the sweep line</param>
    ''' <param name="SweepLine">Y position of the sweep line</param>
    ''' <returns>Calculates the distance fromn a point (NewPoint) to the Parabolic arc generated by the OldPoint and the Sweep line</returns>
    ''' <remarks>The Function only gives you the Y value of the position on the parabolic intersection given the X location</remarks>
    Private Function Intersection2(ByVal NewPoint As Point, ByVal OldPoint As Point, ByVal SweepLine As Double) As Double
        Dim res As Double
        res = (1 / (2 * ((OldPoint.Y) - SweepLine)))
        res *= (NewPoint.X ^ 2 - 2 * OldPoint.X * NewPoint.X + OldPoint.X ^ 2 + OldPoint.Y ^ 2 - SweepLine ^ 2)
        Return (res)
    End Function


End Class

Creating bondaries for the Voronoi diagram

The bondaies for the Voronoi diagram is just nessecary if you want all the points to have a finite area. The diagram would in fact give the point on the outside of the point collection an infinate area, so we limite the generation of this to a bounded pre-defined rectangle.   

We already assumed that you have sorted the points according to the Y value, but to make this function properly Im going to sort them by the X value also. (That is I dont really need to sort the points, I just need the Y_min and Y_max values and X_min and X_max values, to form the rectangle that limits the site area).  

We see that we have two choises, we can either define the area we are interested in creating the Voronoi diagram before performing the sweep line, or we can calculate the area based on the points you want to create the Voronoi diagram from.  

We will contruct an own class (called boundary) that is general enough to be used on any point collection and is therefore huge, and I'm not going to explain all of it here as it has little to do with construction of Voronoi diagrams.

 Public Class Boundary
        'You cant set these variables outside the function
        Private _TopLeft As New Point
        Private _BottomRight As New Point

        'In case you change the increase the values are stored
        Private pSortedByXdirection, pSortedByYdirection As New PointCollection


        Public ReadOnly Property TopLeft() As Point
            Get
                Return _TopLeft
            End Get
        End Property

        Public ReadOnly Property BottomRight() As Point
            Get
                Return _BottomRight
            End Get
        End Property

#Region "Constructors"
        Sub New(ByVal pTopLeft As Point, pBottomRight As Point)
            _TopLeft = pTopLeft
            _BottomRight = pBottomRight
        End Sub

        Sub New(ByVal SortedByX_directioon As PointCollection, ByVal SortedByYdirection As PointCollection)
            CalculateBondariesFromPointCollection(SortedByX_directioon, SortedByYdirection)
            pSortedByXdirection = SortedByX_directioon
            pSortedByYdirection = SortedByYdirection
        End Sub

        Sub New(ByVal OriginalPointcollection As PointCollection)
            pSortedByXdirection = SortPoints(OriginalPointcollection, True)
            pSortedByYdirection = SortPoints(OriginalPointcollection, False)
            CalculateBondariesFromPointCollection(pSortedByXdirection, pSortedByYdirection)
        End Sub

        Sub New()

        End Sub
#End Region

        ''' <summary>
        ''' Returns a sorted pointcollection based on Lexografically sorting
        ''' </summary>
        ''' <param name="samplepoints"></param>
        ''' <param name="SortByXdirection"></param>
        ''' <returns></returns>
        ''' <remarks></remarks>
        Private Function SortPoints(ByVal samplepoints As PointCollection, ByVal SortByXdirection As Boolean) As PointCollection
            'Create another array so we can keep the original array out of order
            Dim copySamplePoints As Point() = New Point(samplepoints.Count - 1) {}
            samplepoints.CopyTo(copySamplePoints, 0)

            If SortByXdirection Then
                Array.Sort(copySamplePoints, New PointSort(PointSort.Mode.X))
            Else
                Array.Sort(copySamplePoints, New PointSort(PointSort.Mode.Y))
            End If

            Dim result As New PointCollection

            For Each p As Point In copySamplePoints
                result.Add(p)
            Next

            Return result
        End Function

        Private Class PointSort
            Implements IComparer
            Public Enum Mode
                X
                Y
            End Enum

            Private currentMode As Mode = Mode.X

            Public Sub New(ByVal mode As Mode)
                currentMode = mode
            End Sub

            'Comparing function
            'Returns one of three values - 0 (equal), 1 (greater than), -1 (less than)
            Private Function IComparer_Compare(ByVal a As Object, ByVal b As Object) As Integer Implements IComparer.Compare
                Dim point1 As Point = CType(a, Point)
                Dim point2 As Point = CType(b, Point)

                If currentMode = Mode.X Then
                    'Compare X values
                    If point1.X > point2.X Then
                        Return 1
                    ElseIf point1.X < point2.X Then
                        Return -1
                    Else
                        If point1.Y > point2.Y Then
                            Return 1
                        ElseIf point1.Y < point2.Y Then
                            Return -1
                        Else 'Identical points
                            Return 0
                        End If
                    End If
                Else
                    If point1.Y > point2.Y Then
                        'Compare Y Values
                        Return 1
                    ElseIf point1.Y < point2.Y Then
                        Return -1
                    Else 'Y1 = Y2
                        If point1.X > point2.X Then
                            'Compare Y Values
                            Return 1
                        ElseIf point1.X < point2.X Then
                            Return -1
                        Else 'Identical points
                            Return 0
                        End If
                    End If
                End If
            End Function
        End Class

        Private Sub CalculateBondariesFromPointCollection(ByVal SortedByX_directioon As PointCollection, ByVal SortedByYdirection As PointCollection)
            Dim p1, p2, p3, p4 As New Point
            p1 = SortedByX_directioon(0)
            p2 = SortedByYdirection(0)

            'Temporary storage of min and max values in the pointcollection
            Dim Xmin, Ymin, Xmax, Ymax As Double

            If p1.X < p2.X Then
                Xmin = p1.X
            Else
                Xmin = p2.X
            End If

            If p1.Y < p2.Y Then
                Ymin = p1.Y
            Else
                Ymin = p2.Y
            End If

            p3 = SortedByX_directioon(SortedByX_directioon.Count - 1)
            p4 = SortedByYdirection(SortedByYdirection.Count - 1)


            If p3.X < p4.X Then
                Xmax = p4.X
            Else
                Xmax = p3.X
            End If

            If p3.Y < p4.Y Then
                Ymax = p4.Y
            Else
                Ymax = p3.Y
            End If

            'We are going to base the increase at the Width and Height of the rectangle
            'so we are going to performe some calculations in order to make these adjustments
            Dim height As Double = Math.Abs(Ymax - Ymin)
            Dim width As Double = Math.Abs(Xmax - Xmin)

            'Scale the with and height in order to add and substract the values to Y and X
            Dim _height As Double = height * (ProcentIncrease) / 100
            Dim _width As Double = width * (ProcentIncrease) / 100

            'Store the final values
            _TopLeft = New Point(Xmin - _width, Ymin - _height)
            _BottomRight = New Point(Xmax + _width, Ymax + _height)

        End Sub

        Public Sub ReturnRectangle(ByVal can As Canvas)
            Dim p As New Rectangle
            p.Fill = Nothing
            p.StrokeThickness = 2
            p.Stroke = Brushes.Blue

            ' Set the width and height of the Rectangle.
            ' The values can be negative therefore the Math.Abs
            p.Width = Math.Abs(_BottomRight.X - _TopLeft.X)
            p.Height = Math.Abs(_BottomRight.Y - _TopLeft.Y)

            can.Children.Add(p)
            Canvas.SetLeft(p, _TopLeft.X)
            Canvas.SetTop(p, _TopLeft.Y)
        End Sub


        'In reality the value of 50 (width is incresed by the factor 1.5) that would increase the bondaries with 25% on all sides
        ' To use it you simply write in the increase at for instance 40 (percent)
        Private _ProcentIncrease As Double = 50
        Public Property ProcentIncrease() As Double
            Get
                Return _ProcentIncrease
            End Get
            Set(ByVal value As Double)
                _ProcentIncrease = (value)

                'Value is changed we need to update the topmost and bottommost points
                CalculateBondariesFromPointCollection(pSortedByXdirection, pSortedByYdirection)
            End Set
        End Property
    End Class

History

This is enough for now, as all the major concepts are handeled, the only thing left is to construct the final implementation.

There is no code to be downloaded from this article, as I have only dealt with the binary search tree and not gotten to the final implementation. The Binary search tree also needs an own class, like the one Benjamin Dittes used. 

Update:

I decided to include the uncompleited code file, but it does not contain the Binary tree and it is not complete in any way, as the previous code. It is only given so you could test things out for your self, while I work on the next (and hopefully last) article on this subject.

References

The two books from the previous article is still the main source in this article: 

• "Computational geometry: Algorithms and applications", Third edition, 2008, Mark de Berg, Otfried Cheong, Marc van Kreveld and Mark Overmars.    
• "Computational geometry in C", Second edition, 2008, Joseph O'Rourke   

BenDi's implementation is also quite useful:  

http://www.codeproject.com/Articles/11275/Fortune-s-Voronoi-algorithm-implemented-in-C 

He has updated his code and you can download his new version here:  

https://sites.google.com/site/bdittes/FortuneVoronoi.zip  

There is also a link that explains the history and has a detailed mathematical description below: 

http://www.pi6.fernuni-hagen.de/publ/tr198.pdf

http://cgm.cs.mcgill.ca/~mcleish/644/Projects/DerekJohns/Sweep.htm