Introduction
Quite a few maze generation algorithms exist, but randomness plays a central role in most of them. Although these algorithms create challenging mazes, they cannot easily guarantee a certain property in a generated maze. For instance: a constraint of exactly four dead ends. Therefore pure randomness may not be the way to go.
In this article I would focus on circular mazes (see Figure 1), as they have a sense of depth; a player starts at the outermost ring of the maze and makes his way inward ring by ring until the maze is solved by reaching the innermost ring. In this article I present a method which will allow you to construct a circular maze with a set of desired properties.
Background
Let's kick off with some terminology:
Fig 1. Elements.
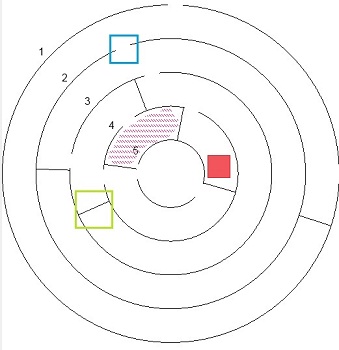
- Blue – door
- Green – barrier
- Red – dead end
- Number – ring level
Main concept
The entire process for creating the maze relies heavily on the tree structure.
The relation between our tree and the maze is as follows:
- Each level (i) of the tree corresponds to a circle (i) in the maze, hence the number of circles in the maze equals the tree's height.
- A tree's node represents a door in a specific ring. For instance, the tree’s root is the entry point into the maze: a single gap in the outermost circle.
- Edges connecting node A at level (i) to node B at level (i+1) will ensure a direct path from ring (i) to an inner ring (i+1).
- A parent node P with two child nodes A and B (or more) will result in a barrier separating each child; this is because the only way of getting from a node in A’s sub-tree to any node in B’s sub-tree is by visiting P.
- A solution for the maze will be a path from the tree’s root to one of the nodes at the lowest level (a node with depth equals to the tree's height).
Fig 2.This maze has two different solutions.

As you can see, a tree completely defines the maze. For example, if we aim to build a maze with six rings, eight dead ends and two different solution paths, we might create the following tree
Fig 3. Tree with eight dead ends, depth of six and two different solutions

Red nodes: dead-end.
Blue nodes: entry points to the innermost ring (final step in the solution)
OK, now that the main idea is in place (Tree -> Maze) how are we going to actually draw a maze based on a given tree? We must figure out the following:
- For each door we'll need to determine its position on its ring.
- For each node at level (i) we’ll need to figure out its segment dimensions, meaning: which part of its inner circle (i+1) it bounds (refer to Figure 1).
Rule of thumb
Calculating door's position and barrier locations (represented by angles) is performed from the innermost ring outwards, using a rule of thumb: when trying to decide on a door’s angle its left and right barriers have already been determined by a previous step.
Nodes at the deepest level are treated specially due to the fact that they have no barriers. For these nodes we’ll begin by dividing the ring into N segments, where N is the number of nodes at the tree’s deepest level. Then, we determine their angle by picking a random angle for each node somewhere within its segment’s boundaries.
For instance: suppose we have three nodes: A, B and C at the deepest level with parent nodes Pa leading to A, Pb leading to B and Pc leading to C, Dividing 360 by 3 creates three segments each 120 degrees in range, One possibility is to position A at 85, B at 146 and C at 300, now we can set boundary values foreach parent node for example Pa’s boundaries could be 0 and 100, Pb’s 100 and 280 lastly Pc’s 280 and 360. For the rest of the nodes at higher levels the rule of thumb applies.
In order to determine a node P’s right and left barriers, we'll inspect each of P’s children's angles to find a maximum and a minimum. P's left barrier must be smaller than the minimum and P's right barrier must be greater than the maximum.
Fig 4. Setting node's parameters (angle and barriers).

Parent node with Id 1 has 3 child nodes with minimum angle of 23 and maximum angle of 308 hence P’s left barrier was set to 22 and its right barrier is 324. A node’s angle must fall somewhere between its right and left barriers, in the above example 196 was picked.
Extending the tree
While traversing upward (leafs to root) we might encounter a node with no children at some level. Such nodes are considered dead-ends and in these cases we’ll be unable to determine the node’s angle due to its missing barriers values. Obviously we'll be unable to continue upwards in order to set its parent barriers.
To solve this issue we expand the tree to a full tree: each leaf node at a level less than the tree’s height will be extended by adding additional nodes until it reaches the tree’s height. Each added node will be marked with a special id so we'll be able to spot and remove these extra nodes at a later stage.
Fig 5. Extending the tree.

Once the tree is extended we can start calculating without the fear of encountering dead-end nodes.
When we're done determining each node's position and its right & left barrier position we'll need to contract the tree back to its original structure. We do this by truncating the specially marked nodes.
Drawing
We're almost done. The actual drawing of the maze is quite easy at this point.
We start by drawing complete circles, one for each of the tree’s levels. Next, we draw arcs on the circles creating doors to go through, and adding barriers within the rings according to angles calculated earlier. Note that we don't need to draw both right and left barriers. One is sufficient, as a barrier of one node is also an end barrier for another.
Fig 6. Maze and its constructing tree

Summarize
- Create a tree to represent your maze.
- Extend the tree (this is how we'll be able to handle dead ends).
- Run the actual calculation which will determine doors and barriers angles.
- Contract tree back to its original structure.
- Draw according to the information stored within the tree nodes.
Limitations
Due to the nature of the algorithm, generated mazes have some limitations. For instance: two doors will never lead to the same dead end.
Paths which solve the maze will never contain a move in which the player backtracks, ie. goes from an inner circle to an outer circle. All moves in a solution's path will be from circle i to circle i+1.
Utilization
Using a tree structure to store information about a maze / map can be extended to keep track of a player in a world. We could fire events to the world enabling it to take action as needed. For instance upon our player enters any node at level “i” create four monsters to attack the player, or regenerate a bigger map when the player solves the current maze.
The code
Although there are open source libraries which implements Graphs / Tree data structures and give the basic algorithms for dealing with them (BFS for instance) I've decided to write my own implementation. One of my main reasons was the need for additional properties to describe a tree node. Also, I've added a number of methods I was missing, but for the most part it was just for the fun of it.
I'm aware of the fact that the code is not perfect (and there's always room for improvement) but i feel like my work is in a decent condition. I've tried to keep the code clear and commented so it should be easy to follow along and understand its flow especially after you've read the above,
Future development
I'm currently missing a convenient way for creating graphs, so for the time being the code takes two inputs: depth and extend which are used to create a connected graph with node count equals to the given depth later on the graph is extended using the extend value.
Another idea would be importing the code for the web; creating fun mazes to solve online.
I hope you've found my method for creating a circular maze as interesting as i have.
For any questions comments please feel free to contact me.
