This article discusses the RSA encryption library with full OAEP padding and private key encryption support.
Introduction
RSA is one of the most important Public key cryptographic algorithms which is keeping the web alive. From secure transactions, secure mail to authentication and certificates, its use is universal.
The basic design of RSA is very simple and elegant and uses simple mathematical operations, yet it is very strong. If used properly, it is nearly impossible to break, given the mathematical complexity of the factoring problem.
The .NET Framework provides native support for RSA and it is pretty useful for most of the purposes. But, for certain cases like some signature schemes, we may require to perform 'private key encryption', which is not natively supported. So, for a project, I had to implement the RSA encryption and decryption from scratch. And, as without proper padding this scheme is vulnerable to attacks, I have also implemented OAEP and PKCS v1.5 padding schemes. This library (RSAx) is fully compatible with the .NET Framework's implementation of RSA.
The Features of the Library
- RSA Encryption and Decryption
- Private Key Encryption Support
- OAEP Padding Support
- PKCS v1.5 Padding Support
- CRT-RSA for fast private key decryption
- Fully Compatible with .NET Cryptography Library
- Uses .NET BigInteger Library
Background
RSA being a public key crypto-system has two keys, the Public key and the Private key. The Encryption is done using one and the decryption is done using the other. Normally, the encryption is done using the Public key and the decryption is done using the Private key. The RSA modulus (explained below) length is called the key length of the cipher. The currently largest factored prime number had 768 bit. As the security of RSA depends on the factoring problem, using a modulus of 1024 bits is a bare minimum. It is recommended to use at least 2048 bits for good security. 4096 bit is pretty much unbreakable, anything beyond 4096 bits is over the top and would also be painfully slow.
Key Generation
- Choose two large random prime numbers P and Q of similar length.
- Compute N = P x Q. N is the modulus for both the Public and Private keys.
- PSI = (P-1)(Q-1) , PSI is also called the Euler's totient function.
- Choose an integer E, such that 1 < E < PSI, making sure that E and PSI are co-prime. E is the Public key exponent.
- Calculate D = E-1 ( mod PSI ), normally using Extended Euclidean algorithm. D is the Private key exponent.
Encryption
- Convert the data bytes to be encrypted, to a large integer called
PlainText. CipherText = PlainText<sup>E</sup> ( mod N )- Convert the integer,
CipherText to a byte array, which is the result of the encryption operation.
Decryption
- Convert encrypted data bytes to a large integer called
CipherText. PlainText = CipherText<sup>D </sup>( mod N )- Convert the integer,
PlainText to a byte array, which is the result of the decryption operation.
Other Considerations
- As its clear that exponents are very large, as a result, the large integers will easily overflow the normal 32 bit '
int' and 64 bit 'long'. To overcome this problem, we require to use a BigInteger library which can handle arbitrarily large numbers. In this case, I used the BigInteger library provided with the .NET Framework (System.Numerics.BigInteger). - The conversion from Byte array to integer and vice-versa are done in a specific format and we have to follow Big-Endian format, I have provided utility functions for conversions via
I2OSP(), and OS2IP().
Padding Schemes
The most critical part of the RSA encryption is the padding scheme. A padding scheme is normally used to increase the length of the plain-text in such a way, that a symmetric algorithm can use it. But, even though the RSA can work without a padding scheme, it is critical for the security of the data, as without proper padding, the cipher-text becomes vulnerable to many different attacks. The padding schemes also brings a randomness to the encrypted data. Every time the data is encrypted, the cipher-text is different, but after decryption, the plain-text remains the same.
There are two major padding schemes in general use, the PKCS and OAEP (Optimal Asymmetric Encryption Padding). PKCS is very simple and is still widely used being an older standard, but, is vulnerable to some newer attacks. OAEP was designed by Bellare and Rogaway to prevent these attacks and is currently recommended for use. But, OAEP is a little complex to implement. I will try to explain the OAEP padding scheme in some detail.
OAEP Padding Scheme
+----------+---------+-------+
DB = | pHash | PS | M |
+----------+---------+-------+
|
+----------+ V
| Seed |--> MGF ---> XOR
+----------+ |
| |
+--+ V |
|00| XOR <----- MGF <-----|
+--+ | |
| | |
V V V
+--+----------+----------------------------+
EM = |00|maskedSeed| maskedDB |
+--+----------+----------------------------+
Figure 1: OAEP Padding Scheme
Keywords
DB - Data block to be encrypted, consists of pHash, PS and M.pHash - Hash of a predefined parameter list in the form of a byte array. It is used to make sure that the parameters at the encryption side and decryption side are the same, but, in most implementations, it's ignored and is optional. In that case, the Hash of an empty byte array is used instead.PS - A string of '0's followed by a 1. Used to fill the unused space in case, the message is shorter than the maximum allowed message length.M - Actual message to be encrypted.Seed - A random array of bytes, the length being equal to the length of hash function being used.MGF - Mask Generation Function, it is used to generate a variable length hash from a given input random input.XOR - Bit-wise Ex-OR operation.maskedSeed - The masked seed, which is part of the padded text. It is later (while decoding) used to get the Seed in conjunction with the MGF output of the maskedDB.maskedDB - The masked Data Block. It is later (while decoding) used to feed the MGF function which is used to obtain the Seed. It is also used to obtain the DB, by using the MGF output of the Seed.
Encoding Prelims
Before encoding, the Hash and the parameter array has to be fixed. For most purposes, the parameter string is an empty byte array. Normally, three different types of hashes are defined by the standard. SHA1, SHA256 and SHA512. SHA1 is default hashing algorithm. Its important that the parameter array and hash algorithm remains same during decoding, otherwise the decoding should fail.
Consider:
hLen = Length of hash function output in bytesk = Length of Modulus in octetsPS_Len = k - MessageLength - 2 * hLen - 2
OAEP Encoding
- Calculate
pHash = HASH(Parameter<code>_Array). - Create an array
PS filled with '0' of length PS_Len . - Create
DB = pHash || PS || 0x01 || M , || means append operation. - Generate a random octet string
Seed of length hLen. - Expand the
Seed using the MGF (explained later) function using the Seed as the input randomness and e output length of (k - hLen - 1) to get dbMask. maskedDB = DB �XOR dbMask seedMask = MGF(maskedDB, hLen)maskedSeed = Seed �XOR seedMask.EncodedMessage = 0x00 || maskedSeed || maskedDB.
That's all. The encoded message is simply encrypted using RSA.
OAEP Decoding
The decoding process is just the opposite of the encoding. Because, the length of the maskedSeed is known, we can easily separate the maskedSeed and maskedDB.
seedMask is generated from maskedDB using MGF, the generated seedMask is XORed with the maskedSeed to get the Seed.
The Seed is expanded using MGF to get dbMask.
dbMask and maskedDB are XORed together to get the DB.
We can easily obtain pHash and M from DB, because the length of pHash is known and the M starts after a sequence of '0's followed by a 1.
If pHash matches with the Hash of the parameter array during decryption, the M is returned as the result. Otherwise, the process fails.
It is important that the decoding algorithm does not allow the user to know the exact nature of the error, otherwise some attacks can be mounted.
The whole point of the OAEP scheme is to make sure that even 1 bit error in decryption renders the complete packet worthless. This is made sure by the hashes, as even a single bit change causes a complete change in the output bits.
MGF Function
Inputs
Z = Initial pseudo-random seedL = Required length of output
Algorithm
for(int loop = 0 ; loop <= Loops ; loop++ )
{
X = Z || (loop in octets array of size 4, BigEndian)
MgfOut += HASH (X);
}
Return first L octets from MgfOut
Screenshots
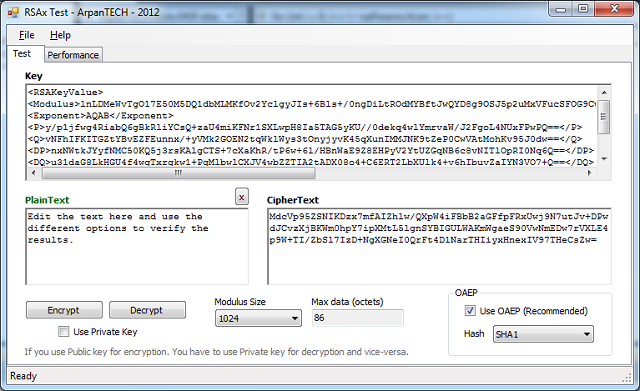
Screenshot 1: Main Window
Showing a test Application for the RSAx library. Any combination of encryption and decryption is allowed, using both Public and Private keys. I have tested the library with keys up to 8192 bits in length. Make sure that different keys (Public and Private) is used for different (Encryption and Decryption) operations, otherwise the decryption will not work properly. While using OAEP, make sure to use the same Hash Algorithm in case of a single Encryption and Decryption. Make sure to Perform File->'Generate Key Pair' after changing the modulus size, for the program to work properly.

Screenshot 2: Test and Performance Window
I've implemented a basic test bench to verify the functioning of the library. It simply encrypts and decrypts random data and verifies the outcome with the expected result. It uses the settings from the previous tab.
Using the Code
Using the library is pretty straightforward.
string PlainText = "Encrypt Me";
string KeyInfo = ".....";
RSAx rsa = new RSAx(KeyInfo, 1024);
byte[] CTX = rsax.Encrypt(Encoding.UTF8.GetBytes(PlainText), true);
string CipherText = Convert.ToBase64String(CTX);
byte[] ETX = Convert.FromBase64String(CipherText);
byte[] PTX = rsax.Decrypt(ETX, true);
string DecryptedString = Encoding.UTF8.GetString(PTX);
The RSAx class can be created from an XML string similar to the native .NET counterpart. It can also be created by using a RSAxParameters class which allows to manually specify the public and the private key parts.
byte [] Modulus = ......
byte [] E = ......
byte [] D = .......
RSAxParameters rsaxParams = new RSAxParameters(Modulus, E, D, 1024);
RSAx rsax = new RSAx(rsaxParams);
It can also be created from a System.Security.Cryptography.RSAParameters structure.
RSA rs = new RSACryptoServiceProvider(1024);
RSAParameters rsa_params = rs.ExportParameters(true);
RSAxParameters rsax_params = new RSAxParameters(rsa_params, 1024);
RSAx rsax = new RSAx(rsax_params);
Private key encryption and Public key decryption can be done as follows:
string PlainText = "Encrypt Me";
string KeyInfo = ".....";
RSAx rsa = new RSAx(KeyInfo, 1024);
byte[] CTX = rsax.Encrypt(Encoding.UTF8.GetBytes(PlainText), true, true);
byte[] PTX = rsax.Decrypt(CTX, false, true);
string DecryptedString = Encoding.UTF8.GetString(PTX);
Points of Interest
Writing the code was pretty straightforward. One interesting thing I found out was that there's a GetNonZeroBytes() function provided in the <code>System.Security.Cryptography.RNGCryptoServiceProvider class, pretty neat! I was just wondering about the internal implementation; if the resultant byte array contains of all non-zero bytes, won't there be some bias in the randomness?
Another thing I realized is that sometimes the RFCs [http://tools.ietf.org/html/rfc3447] are the only source of information about some protocol or algorithm and we have to keep reading it again and again until we understand the whole thing in its entirety.
Sometimes, after the last step of CRT-RSA, the result in the BigInteger was coming negative. And, this negative result plays havoc on the decrypted result. To fix this, I applied a simple hack. Whenever the result is negative, simply add the Modulus N to the result, in order to bring the result back to positive. This is trivial, but it fixed the problem completely.
History
- Version 1.0: First public version
