Project status
This project (originally named "Edumatter® M-12") was a winning submission to The Windows 8* & Ultrabook™ App Innovation Contest (AIC-2012).
Educational software package "Edumatter® M-12" (or simply - Edumatter) for Microsoft Windows® developed by Dr. Alexander Bell (Infosoft International Inc, NY) is intended for public/private school (K-12) and college students, educators, and self-paced education/home schooling.
The application software package ("bundle") contains 2 core applications and one optional app extension:
- Math Calculator and Equation Solver Edumatter M12-L "Light" edition (core app [1], AppUp® download)
- Math Calculator and Equation Solver Edumatter M-12 "Standard" edition (core app [2], AppUp® download)
Core applications (i.e. Edumatter M-12/M12-L) can run on any HW platform equipped with Microsoft Windows OS 7/8 (any edition) in either regular desktop "mouse/keyboard" and/or touch-screen modes. User can download either free "Light" edition or reasonably priced "Standard" edition: the latter included basic tutors' search options.
The application extension ('FindTutor") can operate as a standalone desktop app, extending the functionality of the core applications. It s optimized for novel product line of Ultrabooks™ inspired by Intel Corporation and requires Windows 8 (any edition) and GPS/Gelocation features to be enabled on the client computer in order to provide sophisticates tutors' search option applied to interactive online Microsoft Bing map (technology partially described in the article on Codeproject [8]).
Important note: core applications (Edumatter M-12/M12-L) are well-suited for a wide target auditorium and various age groups. Application extension "FindTutor", which among other features implements real-time GPS/geo-location info retrieval, is intended for a more senior auditorium due to Privacy Protection concerns. Please refer to the "User Manual" and "End User License Agreement" for more details on this rather important issue.
Category 1: Education
Category 2: Productivity
Platform: Desktop app for Win 7/8, any edition
All applications included in the aforementioned software package ("bundle") are available on Intel's AppUp store [1...3]. Sample screenshots are included in this article, and also available as a slide-show in [4].
Ultrabook features to utilize in application
- Touch-screen and keyboard/mouse operation mode
- Geolocation/GPS Sensor to search target/local areas for Math Tutors, SAT, ACT, GED prep, etc.
- Multi-core CPU (i3/i5/i7) to implement efficient parallel algorithms, in particular, prime factoring
- Multi-modal speech-enhanced UI, utilizing high-responsiveness of Ultrabooks and providing Voice messaging to Users via TTS (Text-to-Speech) technology.
Other sales points:
- Unique ability to operate on any combination of fractions, mixed numbers, decimals and integers; results are also displayed as both fractions and decimals.
- Fast Prime-factoring algorithm capable of cracking down up to 18-digit integers.
- Computational efficiency benchmarks on general Math operations, prime factoring and parallel processing algorithms, particular important on HW platform powered by Intel's multi-core CPU
Background
Core application (Edumatter M-12/M12-L) is configured as modular “5-in-1” School Math Calculators and Equation Solvers software package containing 5 modules listed below:
- FC12 Fraction Calculator
- PF12 Prime Factoring Calculator
- LE12 Linear Equation Solver
- SE12 System of Linear Equation Solver
- QE12 Quadratic Equation Solver
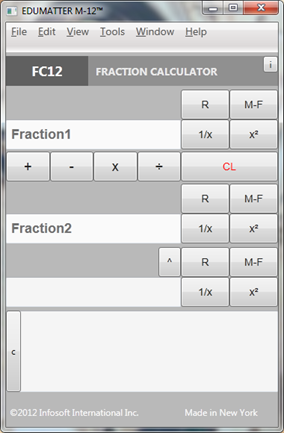
Fig. 1: Edumatter M12 core app, sample screenshot
Each module provides unique capability of processing any combination of fractions (proper/improper), whole or mixed numbers, and decimals. Calculation results are also shown in both fractional and decimal forms except for quadratic equation solver (QE12), which outputs either real or complex numbers in decimal form only (for the obvious reason that the roots of the latter can be irrational numbers).
Fraction Calculator FC12
Fraction Calculator FC12 extends the functionality of the popular online Multiple Fractions Calculator [7] (note: its online counterpart is topping Google search list for many years). Dedicated slideshow is available online at [4]. Coding solutions were partially discussed in Codeproject articles [5,6].
FC-12 can perform binary and unary arithmetic operations on any combinations of whole and mixed number, fractions (proper/improper), and decimal numbers (positive/negative), like: 4, 8.75, 2/3, 9/4, 3 5/7, -6 2/3, 9, 8.75, -12. Any fraction or mixed number can be reduced to the lowest terms. Any improper fraction could be converted to mixed number and vice versa. As an additional convenience feature, all calculation results appear in “History” text box, so they can be copied to computer “Clip Board” memory, or stored in the standard text file for future use.

Fig. 2: Fraction Calculator FC-12, sample screenshot
Prime Factoring Calculator PF12
As a reminder, prime factoring refers to finding non-trivial factors of any positive integer (whole) number, where trivial factors of any whole number are just the number 1 and the number itself. Any other factors are considered non-trivial, for example, number 6 has two non-trivial factors: 6 = 2*3.
Prime Factoring Calculator PF12 implements effective computational algorithm that can perform fast prime factoring of any integer number up to 18 digits (!), essentially unparalleled in any commercially available school math calculators. Results are displayed in calculation history text box and also can be copied to computer “Clip Board” memory, or stored in the standard text file for future use.

Fig. 3: Prime Factoring Calculator PF-12, sample screenshot
Linear Equation Solver LE12
As a reminder, Linear Equation in its canonical form can be written as:
AX + B = C,
where numbers A, B and C are called the coefficients of the equation. The general solution to the Linear equation is: X = (C-B)/A
Linear Equation Solver LE12 is capable of solving linear equation with fractional or whole coefficients. Results are displayed as both fractions and equivalent decimals in calculation history text box, and also can be copied to computer “Clip Board” memory, or stored in the standard text file for future use.
System of Linear Equation Solver SE12
As a reminder, system of linear equations in its canonical form can be written as:
A1X + B1Y= C1
A2X + B2Y= C2
System of Linear Equation Solver SE12 is capable of solving system of linear equations with fractional, decimal or integer coefficients (see sample screenshot #4 included in slide show [1]). Results are displayed as fractions and equivalent decimals in calculation history text box, and also can be copied to computer “Clip Board” memory, or stored in the standard text file for future use.

Fig. 4: System of Linear Equations Solver SE-12, sample screenshot
Quadratic Equation Solver QE12
As a reminder, quadratic equations in its canonical form can be written as: Ax^2+Bx+C=0.
Quadratic Equation Solver QE12 is capable of solving quadratic equations with fractional or whole coefficients. Its output can be either real or complex numbers presented in decimal form only: as we shall know from the theory (see recommended links attached to the article), the solution to quadratic equation might be irrational numbers, thus it could not be presented by any finite fraction. As in all previous cases, calculation results appear in history box and can be copied to computer “Clip Board”, or stored in the standard text file.

Fig. 5: Quadratic Equation Solver QE-12, sample screenshot
Using the code
Core algorithms implemented in Fraction Calculator FC12 were previously published and discussed in the Tip section on Codeproject [5,6]. Fraction arithmetic utilizes novel computation engine, extending existing numeric types with two interrelated classes, namely: Fraction and Mixed Number. The latter is a most universal type combining integer and fractional parts. Following code snippet (Listing 1.) demonstrates implementation details of Fraction class, including its comprehensive error handling, operators overloading and methods overriding techniques:
Listing 1. Implementation details of Fraction class
#region private Vars
private Int64 _n;
private Int64 _d;
#endregion
#region private vars: error msg
private const string errMsgDivBy0 = "Division by 0";
private const string errMsgDenom = "Denominator must be >0";
private const string errMsgNotFraction = "Not a valid Fraction";
private const string errMsgOutOfRange = "Number out of range";
private const string errMsgStackOverflow = "Stack Overflow";
private const string errMsgArithmetic = "Arithmetic error";
#endregion
#region public properties: Numerator and Denominator
internal Int64 Numerator
{
get { return _n; }
set {_n = checked(value);}
}
internal Int64 Denominator
{
get { return _d; }
set
{
if (value <= 0) { throw (new ArgumentException(errMsgDenom)); }
else{ _d = checked(value); }
}
}
#endregion
#region public ctor: Fraction(Int64 N, Int64 D)
internal Fraction() { }
internal Fraction(Int64 N, Int64 D)
{
_n = checked(N);
if (D <= 0) { throw (new ArgumentException(errMsgDenom)); }
else { _d = checked(D); }
}
#endregion
#region Fraction.ToString() override method
public override string ToString()
{
try
{
if (_n == 0) return "0";
if (_d == 1) return _n.ToString();
return (_n.ToString() + "/" + _d.ToString());
}
catch (ArgumentOutOfRangeException) { throw new ArgumentOutOfRangeException(errMsgOutOfRange); }
catch (DivideByZeroException) { throw new DivideByZeroException(errMsgDivBy0); }
catch (StackOverflowException) { throw new StackOverflowException(errMsgStackOverflow); }
catch (ArithmeticException) { throw new ArithmeticException(errMsgArithmetic); }
catch (ArgumentException) { throw new ArgumentException(errMsgNotFraction); }
catch { throw; }
}
#endregion
#region Fractions Arithmetic: Operators overload
public static Fraction operator +(Fraction Fraction1, Fraction Fraction2)
{
Fraction ret = new Fraction();
Int64 _lcm;
if (Fraction1.Denominator == 0 || Fraction2.Denominator == 0)
{ throw (new DivideByZeroException(errMsgDivBy0)); }
if (Fraction1.Denominator < 0 || Fraction2.Denominator < 0)
{ throw (new ArgumentException(errMsgDenom)); }
try
{
_lcm = checked (Integers.LCM(Fraction1.Denominator, Fraction2.Denominator));
ret.Numerator =
checked((Int64)(checked (Fraction1.Numerator * (Int64)(_lcm/Fraction1.Denominator)) +
checked (Fraction2.Numerator * (Int64)(_lcm/Fraction2.Denominator))));
ret.Denominator = _lcm;
return ret;
}
catch (ArgumentOutOfRangeException) { throw new ArgumentOutOfRangeException(errMsgOutOfRange); }
catch (DivideByZeroException) { throw new DivideByZeroException(errMsgDivBy0); }
catch (StackOverflowException) { throw new StackOverflowException(errMsgStackOverflow); }
catch (ArithmeticException) { throw new ArithmeticException(errMsgArithmetic); }
catch (ArgumentException) { throw new ArgumentException(errMsgNotFraction); }
catch { throw; }
finally { ret = null; }
}
#endregion
Prime Factoring PF-12 module implements novel parallel algorithm, efficiently utilizing the power of Ultrabooks multi-core CPU (like i3/i5/i7) to speed up prime factors calculations. Following code snippet (Listing 2) demonstrates the parallel implementation of "find first non-trivial factor" algorithm, which provides significant performance improvement vs. serial implementation in case of factoring big primes:
Listing 2. Fast parallel algorithm to find first non-trivial factor of integer number (Int64)
#region GetFirstFactorParallel(Int64 Num) algorithm
internal static Int64 GetFirstFactorParallel(Int64 Num)
{
ConcurrentStack<Int64> _stack = new ConcurrentStack<Int64>();
ParallelOptions _po = new ParallelOptions();
try
{
Int64 _ret = 1;
if (Num % 2 == 0) return 2;
if (Num % 3 == 0) return 3;
#region parallel algo to find first non-trivial factor if exists
Int64 _upMargin = (Int64)Math.Sqrt(Num) + 1;
int _countCPU = System.Environment.ProcessorCount;
_po.MaxDegreeOfParallelism = _countCPU;
Parallel.For(0, 2, _po, (i, _plState) =>
{
int _seed = 5 + 2 * i;
for (Int64 j = _seed; j < _upMargin; j += 6)
{
if (_stack.Count != 0) { break; }
if (Num % j == 0)
{
if (_stack.Count == 0) { _stack.Push(j); }
break;
}
}
});
#endregion
return (_stack.TryPop(out _ret)) ? _ret : 1;
}
catch { throw; }
finally { _po = null; _stack = null; }
}
#endregion
Important: this parallel algo requires library references:
using System.Collections.Concurrent;
using System.Threading.Tasks;
For smaller integers (less than 10-digits), serial implementation may provide better performance than parallel algorithm described above due to thread synchronization and control logic overhead in the latter one. Following code snippet (Listing 3) demonstrates serial implementation of the efficient prime factoring algorithm:
Listing 3. Fast Prime Factoring Algorithm of integer numbers (Int64), serial implementation
#region PrimeFactoringSerial(Int64 Num) algorithm
internal static List<Int64> PrimeFactoringSerial(Int64 Num)
{
List<Int64> _lstFactors = new List<Int64>();
Int64 _num = Num;
#region factorize on base 2
while (_num % 2 == 0)
{
_lstFactors.Add(2);
_num = (Int64)(_num / 2);
}
if (_num == 1) { return _lstFactors; }
#endregion
#region try factoring in range: 3 ... Math.Sqrt(_num) + 1;
Int64 _upMargin = (Int64)Math.Sqrt(_num) + 1;
for (Int64 i=3; i<=_upMargin; i+=2)
{
if (_num % i == 0)
{
_lstFactors.Add(i);
_num = (Int64) (_num / i);
_upMargin = (Int64) Math.Sqrt(_num) + 1;
i-=2;
}
}
_lstFactors.Add(_num);
_lstFactors.Sort();
return _lstFactors;
#endregion
}
#endregion
FindTutor-2013 application extension implements solution utilizing Microsoft Bing map technology, partially described in Codeproject article [8].
Geolocation/GPS features and Custom map search
FindTutor-2013 application utilizes novel Geolocation/GPS features of Ultrabooks that allows retrieval of geographic coordinates (Latitude, Longitude and optional accuracy) in real-time mode. These coordinates are used to identify a center of POI (points of interest) search area (application also allows manual entry of said coordinates). In order to obtain a set of POI to show up as standard/custom pushpins on the map in the search area, the coordinates of its central point are encoded in web query request to be sent to its online web counterpat, powered by Microsoft Bing mapping technology [8,9].
Microsoft Bing maps implement its own standard "Find What" feature, that allows finding POI in a search area specified by its central point [9]. This standardized Bing Map search is extended with custom search engine based on proprietary database of POI and great-circle (orthodromic) distance computation module [10,11]. Corresponding POI are shown on the map as added custom pushpins of different style and sizes.
Core methods of said engine perform computation of the great-circle distance on Earth between 2 geographical points specified by their Latitude and Longitude: Lat1, Lon1 and Lat2 , Lon2, correspondingly. There are plenty of computational methods described in various online resources (e.g. [12, 13]. One of the popular methods is based on so-called Haversine formula. Following code snippet (Listing 4.) demonstrates speed-optimized C# implementation of this formula:
Listing 4. Haversine formula to calculate great-circle distance between two points on Earth
#region private: const
private const double _radiusEarthMiles = 3959;
private const double _radiusEarthKM = 6371;
private const double _m2km = 1.60934;
private const double _toRad = Math.PI / 180;
#endregion
public static double DistanceMilesHaversine(double Lat1,
double Lon1,
double Lat2,
double Lon2)
{
try
{
double _radLat1 = Lat1 * _toRad;
double _radLat2 = Lat2 * _toRad;
double _dLatHalf = (_radLat2 - _radLat1) / 2;
double _dLonHalf = Math.PI * (Lon2 - Lon1) / 360;
double _a = Math.Sin(_dLatHalf);
_a *= _a;
double _b = Math.Sin(_dLonHalf);
_b *= _b * Math.Cos(_radLat1) * Math.Cos(_radLat2);
double _centralAngle = 2 * Math.Atan2(Math.Sqrt(_a + _b), Math.Sqrt(1 - _a - _b));
return _radiusEarthMiles * _centralAngle;
}
catch { throw; }
}
Notice that the computation of the great-circle distance essentially requires finding a central angle (_centralAngle); multiplying it by the radius of the Earth (_radiusEarthMiles = 3959, or _radiusEarthKM = 6371) will result in said distance.
Another well-known formula that utilizes Spherical law of cosines as described in [14] results in a slightly simplified coding technique: just a single line of code needed for the calculation of central angle (_centralAngle). Following code snippet (Listing 5) provides speed-optimized C# implementation of this formula:
Listing 5. Spherical law of cosines formula to calculate great-circle distance between two points on Earth
public static double DistanceMilesSLC( double Lat1,
double Lon1,
double Lat2,
double Lon2)
{
try
{
double _radLat1 = Lat1 * _toRad;
double _radLat2 = Lat2 * _toRad;
double _radLon1 = Lon1 * _toRad;
double _radLon2 = Lon2 * _toRad;
double _centralAngle = Math.Acos(Math.Sin(_radLat1) * Math.Sin(_radLat2) +
Math.Cos(_radLat1) * Math.Cos(_radLat2) * Math.Cos(_radLon2 - _radLon1));
return _radiusEarthMiles * _centralAngle;
}
catch { throw; }
}
For relatively small search areas (with radius <200 miles), good accuracy and high speed of computation due to minimal use of triginometric functions, can be achieved by using Spherical Earth projection to a plane formula that applies Pythagorean Theorem as described in [11]. Following code snippet (Listing 5) demostrates speed-optimized C# implementation of this algorithm, that was selected for use in the custom geographical search engine (part of FindTutor-2013 app):
Listing 5. Great-circle distance calculation using Spherical Earth projection formula
public static double DistanceMilesSEP(double Lat1,
double Lon1,
double Lat2,
double Lon2)
{
try
{
double _radLat1 = Lat1 * _toRad;
double _radLat2 = Lat2 * _toRad;
double _dLat = (_radLat2 - _radLat1);
double _dLon = (Lon2 - Lon1) * _toRad;
double _a = (_dLon) * Math.Cos((_radLat1 + _radLat2) / 2);
double _centralAngle = Math.Sqrt(_a * _a + _dLat * _dLat);
return _radiusEarthMiles * _centralAngle;
}
catch { throw; }
}
Speech enhancement (TTS)
User Interface (UI) implements optional speech-enhancement features, providing Voice instructions to Users via TTS (Text-to-Speech) technology; this option can be turned On/Off.
Benchmarks
Core applications Edumatter M-12/M12-L include 3 proprietary performance benchmarks, providing the number-crunching efficiency estimates of the client computer, namely:
- General Math
- Prime Factoring
- Parallel Processing algorithm efficiency on Intel i3, i5 or i7 multi-core CPU architecture
Points of Interest
Product availability and compatibility
Core applications "Edumatter M-12/M12-L" are fully compatible with Microsoft Windows 7 or 8, and is optimized to run on Ultrabooks™ (inspired by Intel) hardware platform. It’s backward compatible with previous versions of Windows Vista/XP.
Speech Technology
Edumatter M-12/M12-L core applications and application extension FindTutor implement multi-modal Voice-enhanced User Interface, utilizing Microsoft Speech object library, in particular, TTS (Text-to-Speech) technology set, providing Voice instructions and error messaging to the User. As per actual testing, it was found that TTS greatly benefits from Ultrabooks high internal data rate (due to sophisticated duo SSD/SATA), noticeably reducing the Voice response latency and increasing overall UI responsiveness.
Digitally Signing Microsoft Visual Studio 2010 executable (.exe) and setup (.msi) files
Adding digital signature to Visual Studio output files with Digital Certificate obtained from Certificate Authorities (CA) was found not just a trivial task. The issue is not pertinent just to particular CA (in this case, Comodo [15]), but is rather common to Visual Studio projects (version 2010 was used for Setup projects, that generate installable .msi files). The standard and most intuitive "way of least resistance" of going to Project->Properties -> Signing tab and just entering a strong name key file (which can be, for example, CertificateFile.pfx received from CA) failed with error message like "Cannot import the following key file: CertificateFile.pfx. The key file may be password protected. To correct this, try to import the certificate again or manually install the certificate to the Strong Name CSP with the following key container name...". Obviously, the file CertificateFile.pfx is and must be protected. So, after hours of Google and numerous "try-error" attempts it became clear that one of the most reliable and straightforward ways to sign VS project outputs (.exe and/or .msi) is to use command line [16] added to post build events that utilizes signtool.exe (latter is included in Microsoft SDK [17], that can be downloaded for free) like shown in the following examples:
Digitally Signing .exe files in VS 2010 using signtool.exe and command line
In Visual Studio 2010 Project (the same technique can apply to VS 2012), open Properties->Build Events tab. In "Post-build event command line" text-box, add the command, which should look like the following (notice that command is pointing to "obj" dir, not "bin"):
"%ProgramFiles%\Microsoft SDKs\Windows\v7.0A\Bin\signtool.exe" sign /n [Company Name] /f C:\CA\CertificateFile.pfx /p password /t http://timestamp.comodoca.com/authenticode "$(ProjectDir)obj/x86/Release/YourProduct.exe"
Digitally Signing .msi files in VS 2010 using signtool.exe and command prompt
In Visual Studio 2010 Setup Project, find the item "PostBuildEvent" in Solution Explorer, and enter command line similar to the one shown below:
"%ProgramFiles%\Microsoft SDKs\Windows\v7.0A\Bin\signtool.exe" sign /n "Infosoft Intl Inc" /f C:\CA\CertificateFile.pfx /p password /t http://timestamp.comodoca.com/authenticode "$(ProjectDir)Release/Setup.msi"
Note, that [Company Name] like "Infosoft Intl Inc" shown in the sample above is just an optional parameter and can be omitted. TimeStamp server in these examples corresponds to aforementioned CA Comodo [15]; certificate file name/location (C:\CA\CerticateFile.pfx) are shown for demo purpose only.
ALS Sensor use-case
Core applications Edumatter M-12/M12-L are potentially capable of automated style selection, for example switching between High/Low contrast color scheme based upon data feed from the ambient light sensor (ALS), included in some high-end Ultrabooks. The possible implementation will require some sort of programmatic equivalent of "comparator w/hysteresis" (well- known in Electrical Engineering) observing ALS data stream and automatically switching between styles based upon some predefined luminance threshold(s). Upon serious design consideration and partial prototype testing, such automatic control feature was found unnecessary in this type of applications: "irrational exuberance", i.e. artificial overstretching of sensors use-cases can potentially result in continuous "styles jitter", thus increasing the annoyance/eye-irritation and degrading the overall user experience rather than improving it. Alternatively, the style selection feature was implemented as a simple menu option (refer to the manual for details).
Real-life design considerations
As mentioned above, core applications (Edumatter M12/M12-L) are well suited for a wide target auditorium and various age groups. To the contrary, application extension "FindTutor-2013", which among other features implements real-time GPS/geolocation info retrieval, which could be potentially interpreted as "personally-identifiable information" and as such, is considered to be a sensitive information, is intended for a more senior auditorium due to Privacy Protection concerns. Please refer to the "User Manual" and "End User License Agreement" (EULA) for more details on this rather important issue, in particular, "Privacy Policy" statement in EULA.

Fig. 6: Real-time geolocation features of Ultrabooks

Fig. 7: Sample screenshot of the web page w/Bing map showing Tutors nearby
Online Calculators
As mentioned above, Fraction Calculator FC12 has its free online counterpart with limited features placed in public domain. Other computational modules pertinent to this application are also available online at webinfocentral.com. Comparing pros and cons of “both worlds”, i.e. desktop apps vs. online web apps: Edumatter M-12 implemented as regular desktop application for Microsoft Windows does not require live Internet connection and provides much better performance and overall user experience than its online web-based counterparts. On the other hand, it requires one-time product installation and activation on particular client’s computer running Microsoft Windows, while web-based applications are universally accessible via any digital platform equipped with web browser. It's relevant to mention that desktop and web applications are not mutually exclusive, so they can successfully coexist in digital education domain, effectively complementing each other.
References
- Fast Integer Algorithms: GCD and LCM (CodeProject article)
- Fast Greatest Common Divisor (GCD) Algorithm
- Bing Maps Interactive SDK
- Geographical distance (wiki)
- Great-circle distance (wiki)
- Central angle (wiki)
- Haversine formula (wiki)
- Spherical law of cosines (wiki)
History
- "Edumatter M12-L" Light" edition v. 8.1.3 has been published on the Intel's AppUp store (11/19/2012)
- "Edumatter M-12" "Standard" edition v. 8.1.4 has been published on the Intel's AppUp store (11/28/2012)
- "FindTutor" app extension version 8.1.1 has been published on the Intel's AppUp store (11/26/2012)
- "Edumatter-814" Standard for Windows 7/8, v. 8.1.4.1 has been released in Aug-2014
