Introduction
This article focuses on how to calculate the absorption coefficient by placing porous absorbers in front of a wall or other hard surfaces. This means that if you want to construct
an absorber of mineral wool of your own, in you home studio, garage or any other a room, you could use the calculated values and use them in calculating the reverberation time (which you
can read more about here:
This is quite a narrow article, but it's an important aspect of many rooms, and how they will behave. It is also necessary to have knowledge of these these properties
when you want to calculate more advanced features in a room, and use it for sound reproduction.
Background
There are two different main paths you could follow when you want to calculate the absorption and the complex wavenumber in a porous absorber.
They both use the dimensionless parameter E and that is defined by the equation below:
One should take note that the p0 is usually set to the weight of air, as most porous absorbers have roughly 98 % air in them. The Flow resistivity is often given in datasheets
as MKS rayl m-1, and this is one of the most important parameters in the equation, so it's important to know how to find it.
The two researchers Delany and Bazley published a formula for approximating based on the averages of many normal porous absorbers. The formula
they published gave one for the wavenumber and one for the characteristic impedance, and these two are given below:
These formulas can be used in mid and high frequency without any problems, but they fail at the low frequency. Luckily Mechel developed a different formula, using measurement
for the mid and high frequencies and a theoretical model for the low frequencies. The formulation for the low frequency part are as follows:
Where the is the adiabatic constant for air, roughly equal to 1.4,
and the is the porosity of the material, usually in the area around 0.98, meaning the absorber contains roughly
98 % air in its volume. The normal, or formulas valid for the mid and high frequencies are given below:
Mechel also sets some boundaries for where the transmission between the two different formulas interact, these are given in the program and not discussed here.
The implementation of that would give out a class containing these two parameters are given below:
Module Porous
Public Function DelanyBazely(ByVal Frequency As Double, ByVal FlowResistivity _
As Double, Optional ByVal rho As Double = 1.21, Optional ByVal c As Double = 340) _
As Acoustics.SimpleMaterialPropertiesHolder
Dim result As New Acoustics.SimpleMaterialPropertiesHolder
Dim E As Double = rho * Frequency / FlowResistivity
result.CharacteristicImpedance = rho * c * (1 + 0.0571 * Math.Pow(E, -0.754) - New Complex(0, 0.087 * Math.Pow(E, -0.732)))
result.PropagationCoeficcient = New Complex(0, 2 * Math.PI * Frequency / c)
result.PropagationCoeficcient *= (1 + 0.0978 * Math.Pow(E, -0.7) - New Complex(0, 0.189 * Math.Pow(E, -0.595)))
Return result
End Function
Public Function Mechel(ByVal Frequency As Double, ByVal FlowResistivity As Double, _
Optional ByVal Porousity As Double = 0.98, Optional ByVal Adiabat As Double = 1.4, _
Optional ByVal rho As Double = 1.21, Optional ByVal c As Double = 340) _
As Acoustics.SimpleMaterialPropertiesHolder
Dim E As Double = rho * Frequency / FlowResistivity
Dim lessPart As New Acoustics.SimpleMaterialPropertiesHolder
lessPart.PropagationCoeficcient = New Complex(0, 2 * Math.PI * Frequency / c)
lessPart.PropagationCoeficcient *= Complex.Sqrt(New Complex(1, -Adiabat / (2 * Math.PI * E)))
lessPart.CharacteristicImpedance = New Complex(0, -rho * c ^ 2 / (2 * Math.PI * Frequency * Adiabat * Porousity))
lessPart.CharacteristicImpedance *= lessPart.PropagationCoeficcient
Dim NormalPart As New Acoustics.SimpleMaterialPropertiesHolder
NormalPart.PropagationCoeficcient = New Complex(0.2082 * E ^ (-0.6193), 1 + 0.1087 * E ^ (-0.6731))
NormalPart.PropagationCoeficcient *= New Complex(2 * Math.PI * Frequency / c, 0)
NormalPart.CharacteristicImpedance = New Complex(1 + 0.06082 * E ^ (-0.717), -0.1323 * E ^ (-0.6601))
NormalPart.CharacteristicImpedance *= rho * c
Dim FinalResult As New Acoustics.SimpleMaterialPropertiesHolder
FinalResult = NormalPart
If E > 0.04 Then
Return FinalResult
End If
Dim Elimit As New ElimitHolder
If E < Elimit.GammaReal Then
FinalResult.PropagationCoeficcient = _
New Complex(lessPart.PropagationCoeficcient.Real, _
FinalResult.PropagationCoeficcient.Imaginary)
End If
If E < Elimit.GammaImg Then
FinalResult.PropagationCoeficcient = _
New Complex(FinalResult.PropagationCoeficcient.Real, _
lessPart.PropagationCoeficcient.Imaginary)
End If
If E < Elimit.Zreal Then
FinalResult.CharacteristicImpedance = _
New Complex(lessPart.CharacteristicImpedance.Real, _
FinalResult.CharacteristicImpedance.Imaginary)
End If
If E < Elimit.Zimg Then
FinalResult.CharacteristicImpedance = _
New Complex(FinalResult.CharacteristicImpedance.Real, _
lessPart.CharacteristicImpedance.Imaginary)
End If
Return FinalResult
End Function
Private Class ElimitHolder
Public GammaReal As Double = 0.04
Public GammaImg As Double = 0.008
Public Zreal As Double = 0.006
Public Zimg As Double = 0.02
End Class
End Module
Mechel has given other more complicated formulas leather, that includes the effect of among other things curtains, were you don't know the porosity and that would need
to be calculated in order to arrive at the correct formulas for propagation constants and characteristic impedance.
There are also alternatives to the two methods
that I have just shown, namely the Rayleigh model, which uses a purely theoretical approach and is similar to Mechels low frequency formula, by assuming that a porous absorber
could be modeled as a matrix of tubes or a perforated plate.
Mechel also have a different formula that separates different types of mineral wool.
He separates Glass fibers,and mineral fibre (basalt or rock wool), and gives two different expressions for it. It is however given in the book "Acoustic absorbers
and diffusers", and Mechel gives a full account of different ways of calculation porous absorbers in "Formulas of acoustic" (his account is on roughly 50 pages,
and that is just intended to be a formula reference book!)
There are also two more models, one by Attenborough and one by Allard and Johnson,
the model of Allard and Johnson do however use some of the results from Attenborough in their formulas. These are relative complex models that take more parameters into
account when calculating the properties of the medium. I may revisit this article in the future and expand it to include their model as well.
How to do calculations
This is actually just as difficult as calculating the coefficients of the porous materials used in the equation.
We need to start off with some theory first.
A layer in front of an infinitely reflecting surface would always have a surface impedance that could be expressed the following way:
Take note that we are here talking about the wave number and not the propagation coefficient (the difference
is Propagation coefficient = jk. So if we have the propagation coefficient we need to multiply it by -j in order to get the wave number, which, confusingly enough could
be complex in itself.)
Once we have the surface impedance of this simple material we would then proceed by calculating the reflections from our material relative
to the air in front of the material:
This represents the reflection, but we are interested in the losses
so we must take 1 - the reflected wave to find out how much of the energy is depleted. And in acoustics the reflection factor is meant to be the amplitude
of the reflected wave, and we want the changes in intensity, which is proportional to the pressure squared. This is called the absorption factor and is calculated as shown below:
The formulation calculates the normal incident of a sound wave, meaning that it does not take into account a diffuse waves that are encountered in rooms.
Using the code
The code that calculates the absorptions coefficient are as follows:
Public Function CalcualtePorousAbsorption(ByVal Sigma As Double, _
ByVal ThicknessOfPorousAbsorber As Double, ByVal DelanyBazely As Boolean) As OctaveBand
Dim Result As New OctaveBand
Dim c As Double = 340
Dim rho As Double = 1.21
Dim z0 As Double
z0 = c * rho
For i As Integer = 0 To Result.Count - 1
Dim f As Double = Result.Okt13(i)
Dim MaterialProperties As New SimpleMaterialPropertiesHolder
If DelanyBazely Then
MaterialProperties = Acoustics.Materials.DelanyBazely(f, Sigma)
Else
MaterialProperties = Acoustics.Materials.MechelGrundmann(f, Sigma)
End If
Dim z As New Complex(0, -1)
z *= MaterialProperties.CharacteristicImpedance / _
Complex.Tan(MaterialProperties.PropagationCoeficcient * z * ThicknessOfPorousAbsorber)
Dim ReflectionCoefficient As New Complex
ReflectionCoefficient = (z - z0) / (z + z0)
Result.Item(i) = 1 - (Complex.Abs(ReflectionCoefficient)) ^ 2
Next
Return Result
End Function
And that completes the application.
History
- 12.10.2012 - Initial release.
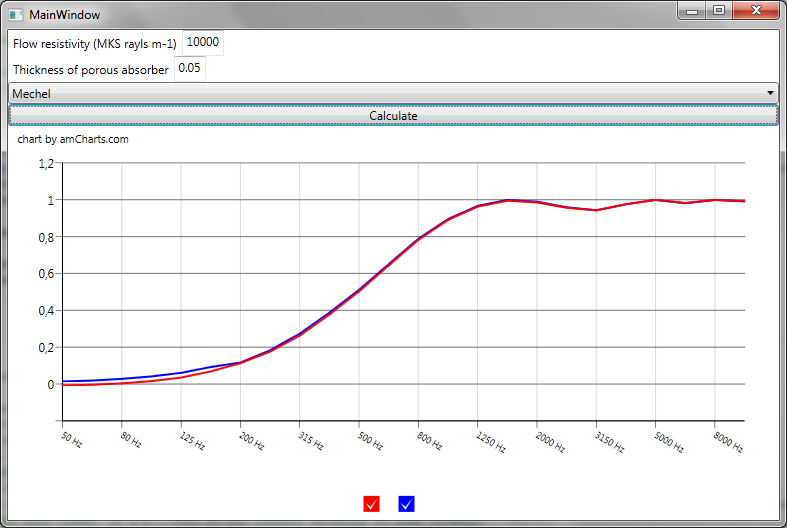
If you take a look at the two different types of calculation the absorption from a layer of porous material backed by a hard wall, you don't see much difference,
except at the low frequency range. Normally Delany-Bazley are considered valid from 250 Hz and above, so it's normally always advisable to use Mechels formula instead.
References
The books I list here offers a good explanation of what I describe, and are good further references if you want to know more. They are listed in the order of how much I have
used them in the article.
- "Building acoustics", First edition (2008), Tor Erik Vigran, CRC Press
- "Acoustic Absorbers and diffuseres - Theory, design,
and application", Second edition (2009), Trevor J. Cox and Peter D'Antonio, Taylor & Francis.
- "Formulas of Acoustics", 2nd Edition, F.P. Mechel, Springer
- "Fundementals of Acoustics", Fourth edition,
Kinsler, Frey, Coppens and Sanders, John Wiley & Sons, Inc.
