The audience of this article's readers will find out how to perform association rules learning (ARL) by using the scalable optimized Apriori algorithm, discussed.
Table of Contents
Introduction
An uncategorized data classification is one of the most complex engineering problems, in the field of computer science and IT, while performing the big-data analysis. To classify the potentially huge amounts of an uncategorized data, various approaches and patterns are presently used. Specifically, these patterns basically include the number of computer algorithms such as k-means clustering procedure, naïve Bayesian algorithm, artificial neural networks (ANNs), etc. Each one of these approaches allows to solely classify the data of a specific kind. For example, k-means and CLOPE-clustering can be used to perform a classification of data represented as a n-dimensional vectors of numerical parameter values. In turn, naïve Bayesian algorithm is intended to be used for classifying the either numerical or other sorts of data, only in case when a discrete tuple of classes (e.g., mostly a set of “two” classes) has already been pre-defined. Also, the ANNs are mostly capable of performing a classification and generalization, which makes it perfect for solving any of existing problems, in which we basically deal with the classification of typically small amounts of data.
Unfortunately, due to its nature, none of these methods mentioned above can be used as a single algorithm for classifying the data of the various structures, especially those data that must be arranged into one or multiple of hierarchies.
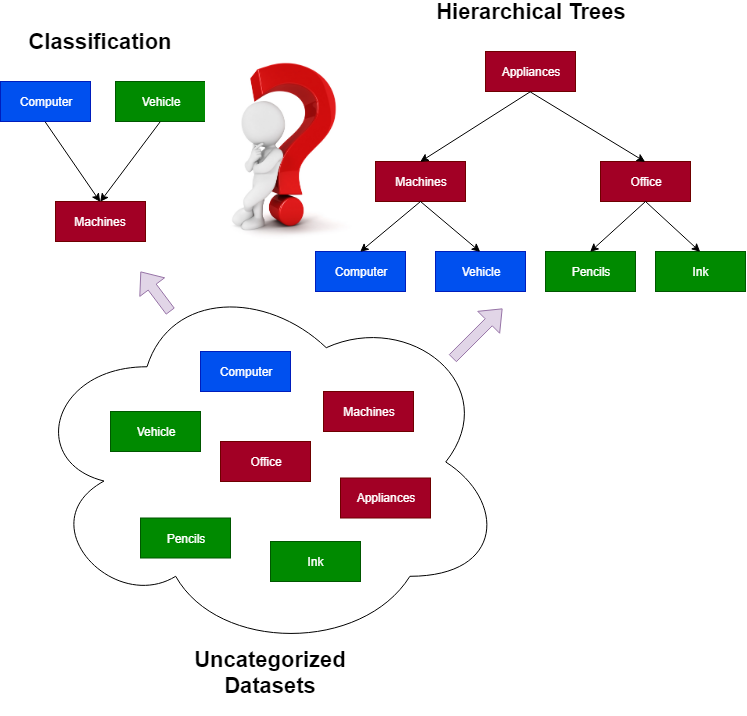
As well, there’s the number of issues using these algorithms while performing a real-time processing of the dynamic data streams, in which the amounts of transactional data are drastically growing. In case of using k-means clustering, we typically have a need to re-compute the data model for each portion of new data sent to a dynamic data stream. As you might have already known, k-means is a complex computational task, which is above NP-hard, exhausting the sufficient amounts of CPUs and system memory resources. Similarly, ANNs must also be re-trained after receiving the new amounts of transactions from the dynamic data streams, which leads to the same problem as when the k-means or CLOPE-clustering algorithms are used.
Here’s a vivid example of a classification problem while solving which neither k-means nor naïve Bayesian classifiers can be useful. Suppose we deal with a dynamic real-time processing stream, in which the entire data is arranged into transactions $\begin{aligned}T=\{t_1,t_2,t_3,…,t_{n-1},t_n\}\end{aligned} $. Each transaction $\begin{aligned}∀t_s\end{aligned} $ is a set of items, which values can be of either numerical, string, object or any other existing type of data. Moreover, we’re given a set of (i.e. more than “two”) pre-defined classes $\begin{aligned}C=\{c_1,c_2,c_3,…,c_{m-1},c_m\}\end{aligned} $. In this case, our goal is to perform a trivial classification by distributing particular items $\begin{aligned}\forall i_k \in I \end{aligned}$ retrieved from the set of transactions between those specific classes $\begin{aligned}C\end{aligned} $.
Obviously, that, in this case, we need an absolutely different approach for classifying the various of an uncategorized data, rather than the conventional k-means clustering or naïve Bayesian classification.
In data mining and AI machine learning, there’s the number of algorithms that allow to quickly and easily classify an uncategorized data of various types arranged into a set of transactions by performing association rules learning (ARL). This number of algorithms basically includes a famous brute-force algorithm as well as a series of its optimized modifications formulated as Apriori, ECLAT and FPGrowth. The following algorithms belong to an entire family association rules learning (ARL) and big-data processing algorithms.
Unlike the other classification algorithms, these algorithms allow to perform classification that basically relies on the process of determining associations between specific data, including their hierarchical relations, that are exhibited on the entire dataset represented as an input sets of transactions.
In this article, we will introduce and formulate the well-known Apriori algorithm that is a good alternative to any of other existing classification algorithms while processing a big-data of various types, as well as providing an efficient optimization of the original brute-force associations mining algorithm. We will ground our discussion to the aspects of using the Apriori algorithm to classify items of string data type from a given set, creating groups of items belonging to each particular class, based on the statistical data that can be learned from a given set of transactions.
In the background section of this article, we will discuss about the association rules learning (ARL) process fundamentals, providing a better understanding of specific terms as a part of the association rules mining problem definition. After that, we will introduce and formulate Apriori algorithm step by step. Finally, we will thoroughly discuss about the implementation of Apriori algorithm using Intel C++ Compiler 19.0 and OpenMP performance library. At the end of our discussion, we will evaluate the Apriori algorithm and take a closer look at what particular results can be achieved by using this algorithm.
Background
Association Rules Learning Fundamentals
Association Rules Learning (ARL) is one of the most essential strategies of data mining and big-data analysis process. It becomes very useful and efficient whenever we have a need to process typically huge amounts of data represented in a string format and no other information is provided. Another benefit of involving association rules mining approach is its “talent” of performing an optimized processing of a normally huge dynamic data streams, gaining insights, trends and knowledge on the data being analyzed in near real-time.
A data stream is a huge collection of various data generated by one or many providers. In the most cases, data streams are created as the result of performing the series of real-time transactions committed by a specific data processing and streaming functionality. Once a transaction has been committed and being processed, we normally receive a resultant set of data sent to a data stream, that is also called a “transaction”. There’re various transaction implications such as either financial, trading or gaming. For example, we receive the specific data on the number of goods purchased from a department store as the result of performing a trading transaction. In this case, these data are represented as an itemset, each item of which is an entity containing the information about the name of a particular product being purchased and its price, such as:
| ID | Product | Price |
| 1 | Bread | $2.00 |
| 2 | Milk | $5.99 |
| 3 | Honey | $6.79 |
| 4 | Salad | $4.67 |
Normally, an average department store commits billions of transactions sent to a data stream. The enormously huge amounts of transactional data makes it possible to reveal the vast of insights and trends exhibited on the data being collected in the real-time.
For example, by using the big-data analysis algorithms, we can find out about the popularity of specific products as well as determine what particular products were purchased together the most often, based on the relationship between certain statistical data mined. The association rules learning algorithms are mostly recommended for that purpose, rather than the primitive frequency tests or other classification algorithms.
“In 1992, the Teradata retail consulting group led by Thomas Blishock conducted a study of 1.2 million transactions in 25 stores for the Osco Drug retailer. After analyzing all these transactions, the strongest rule was “Between 5:00pm and 7:00pm most often beer and diapers are bought together. Unfortunately, such a rule seemed so counterintuitive to the leadership of Osco Drug that they did not put diapers on the shelves next to the beer. Although the explanation for the pair of beer-diapers was quite to be found when both members of the young family were returning home from work (just by 5:00 pm), the wives usually sent their husbands for diapers to the nearest store. And the husbands, without hesitation, combined the pleasant with the useful - they bought diapers on the instructions of the wife and beer for their own evening pastime”.
In the next paragraph, we will introduce itemsets and transactions and take a closer look at what specifically insights and trends might be exhibited on the data within an entire data stream.
Sets Of Transactions
At this point, let’s provide an explanation of some terms, required for a better understanding of the association rules mining process.
An “Itemset” $\begin{aligned}I=\{i_1,i_2,i_3,…,i_{n-1},i_n\}\end{aligned} $ is a sequence of items $\begin{aligned}\forall i_k \in I \end{aligned} $, the string values of which represent specific entities. For example: $\begin{aligned}I=\{"Computer" ,"Office" ,"Vehicle" ,"Beer" ,…,"Bread" ,"Diapers" \}\end{aligned} $. The data items within a single itemset might or might not be associated. Specifically, an itemset is simply a “raw” collection of data. If an itemset consists of k-items, then it’s called k-itemset.
A “Transaction” (defined) ∀t is a resultant itemset, sent to a data stream, after a transaction has been committed and processed. A transaction refers to an itemset containing those items, a certain amount of which might be associated. In the example listed above, “Computer” and “Office”, “Bread”, “Beer” and “Diapers” are associated items, whilst “Vehicle” and “Diapers” are not associated.
A “Set of Transactions” (defined) – a fragment of data stream containing a sequence of itemsets for all transactions committed within a certain period of time. The itemsets of specific transactions in a set might or might not contain the items with the same values. Each item in a particular transaction’s itemset might also appear in the itemsets of other transactions. Similarly, the same associations of items might be included in more than one transaction. If a pair of transactions in the given set contains the same associations, then there’s a possibility that those transactions might also be associated. The example below illustrates a trivial set of transactions being discussed:
| TID | Transaction |
| 1 | Engine, Vehicle, Steering, CPU, Brakes, Motherboard, Machines, Appliances |
| 2 | CPU, Wheels, Tank, Motherboard, Seats, Camera, Cooler, Computer, Machines, Appliances |
| 3 | Motherboard, Steering, Monitor, Brakes, Engine, Vehicle, Machines, Appliances |
| 4 | CPU, Steering, Brakes, Cooler, Monitor, GPU, Computer, Machines, Appliances |
| 5 | Vehicle, Cooler, CPU, Steering, Brakes, Wheels, Tank, Engine, Machines, Appliances |
| 6 | Computer, CPU, Motherboard, GPU, Cooler, Engine, Machines, Appliances |
| 7 | Brakes, Vehicle, Tank, Engine, CPU, Steering, Machines, Appliances |
| 8 | Pens, Ink, Pencils, Desk, Typewriter, Brushes, Office, Appliances |
| 9 | Ink, Typewriter, Pencils, Desk, Office, Appliances |
As you’ve might have noticed in the example above, there’re items and its associations that more or less frequently occur in the specific set of transactions. Also, there’s at least one item that occurs across all transactions in the set.
In the succeeding paragraph of this article, we will thoroughly discuss how the data on the frequency of items and its associations occurrence in a transactions set can be used for association rules mining.
To be able to perform association rules learning (ARL), the entire transaction dataset must conform to at least three requirements:
- An itemset of each transaction must consist of a certain amount of items belonging to a specific “class”, along with another smaller amount of items from one or multiple of classes, other than the specific class;
- The overall amount of items in each itemset must contain those items representing a specific “class” or “category”;
- There must be an item representing the topmost “rooted” class, included in all transaction itemsets;
According to hierarchy principle, an item that occurs in all transaction itemsets is actually a “root” of a tree, and each item representing a class is an “internal” node, interconnecting the specific siblings (i.e., branches). Also, those items that are not representing any of existing classes are “leaf” nodes of the tree.
In one of the next paragraphs, we will thoroughly discuss how to build various of hierarchies based on the resultant data obtained during the association rules mining process.
Association Rules
An “Association Rule” (defined) – an implication of two itemsets, for which there’s a direct, evident and unambiguous relationship between the specific items in these both sets. The first itemset of this implication is called “antecedent”, representing a certain “condition”, whilst the second one – its “consequent”. Logically, an association rule can be denoted as follows: if ‘condition’ is ‘true’, then ‘consequence’ is also ‘true’. As well, an association rule can be interpreted as “From one, another can be concluded”. For example, we’re having a primitive association rule:
{"Computer" ,Monitor}→{CPU,Motherboard}
The expression listed above represents the relationship between specific items (i.e., “entities”). In this case if {“Computer”, “Monitor”} are interrelated, then the specific items such as {“Computer”, “CPU”}, {“Computer”, “Motherboard”}, {“Monitor”, “CPU”}, {“Monitor”, “Motherboard”}, … are having exactly the same relationship. Also, there’s the relationship between pairs of these particular items, mentioned above. We consider that each of these pairs is an association rule related to the other similar rules, as well as to its ancestor rule. Moreover, the “antecedent” of an association rule is also a rule, which is considered to be a “parent” for all variations of subsequent rules derived from the following association rule, illustrated above.
Algebraically, an association rule can be denoted by using the implication operator A→B, where A – antecedent and B – the specific consequent itemset, respectively. As well, A and B are equivalent, which means that A→B≡B→A. The number of theory of set’s operators, such as ∪,∩,⊆,∈,∉ can be applied to any of the association rules. Here’s a few examples:
{Computer,Monitor}∩{CPU,Motherboard}=∅
The following example above illustrates that the intersection of these two itemsets is exactly an empty set ∅. It means that the rule’s antecedent and consequent itemsets can never intersect. This is the requirement for generating the new rules candidates.
{Computer,Monitor}∪{CPU,Motherboard}={Computer,Monitor,CPU,Motherboard}
The second example above, illustrates the union of either antecedent or consequent of the rule. The following technique is primarily used during the new rules’ generation process.
{Monitor,CPU}⊆{Computer,Monitor,CPU,Motherboard},
{Computer,Motherboard}⊆{Computer,Monitor,CPU,Motherboard},
As you can see from the example above, the 2-itemset {Monitor,CPU} is contained within another 4-itemset {Computer,Monitor,CPU,Motherboard}. This actually indicates that these both itemsets have a logical relationship.
Computer∈{Computer,Monitor,CPU,Motherboard},
Beer∉{Computer,Monitor,CPU,Motherboard}
The final two examples state that the item “Computer” belongs to the 4-itemset and has the relationship with the rest of other items within the following itemset. At the same time, the item “Beer” is not included in the following itemset. That’s actually why, it has relationship with none of these items.
There’re the various of methods such as either brute-force or optimized for generating the new sets of rules. Whatever methods are used for mining those rules, the association rules concept is retaining its logical and mathematical sense.
Since we’ve thoroughly discussed about the association rule term and its definition, let’s now take a closer look at the process during which the new rules are being generated. The following example will illustrate an approach, common to the most of association rules mining algorithms, that allows to produce the principally new ones based on the pairs of already existing rules from a given set.
Suppose, we’re already having a pair of N-itemsets $\begin{aligned}I^{'}\end{aligned} $; and $\begin{aligned}I^{''}\end{aligned} $, each one consisting of a certain number of the unique items extracted from itemsets of particular transactions, so that $\begin{aligned}I=\{ \forall i_k | \forall i_k \in t_s, t_s \in T\}\end{aligned} $. To produce a new rule candidate, we need to merge the itemsets if and only if these both sets satisfy the condition that none of these items in $\begin{aligned}I^{'}\end{aligned} $; itemset are included in the second itemset $\begin{aligned}I^{''}\end{aligned} $ ($\begin{aligned}I^{'} \notin I^{''} \end{aligned} $). Here’re the two examples in which a new rule can or cannot be produced:
{Computer,Monitor}⊎{CPU,Motherboard}→{Computer,Monitor,CPU,Motherboard},
{Motherboard,Diapers}⊎{CPU,Motherboard}→∅,
{Computer,Monitor}⊎{Bread,Diapers}→{Computer,Monitor,Bread,Diapers},
In the first example, we can generate a new rule since none of the items in the itemset $\begin{aligned}I^{'}\end{aligned} $ are contained in the itemset $\begin{aligned}I^{''}\end{aligned} $. In spite, the second example illustrates that we normally cannot generate a new rule, in this case, since the item “Motherboard” is included in both itemsets $\begin{aligned}I^{'}\end{aligned} $; and $\begin{aligned}I^{''}\end{aligned} $.
As for the rule from the first example, we can also produce a set of its sibling rules such as:
{Computer,Monitor}⊎{CPU,Motherboard}→{Computer,Monitor,CPU,Motherboard},
{Computer,Monitor}⊎{Bread,Diapers}→{Computer,Monitor,Bread,Diapers},
{Computer,Monitor}→{CPU,Motherboard},
{Computer,CPU}→{Motherboard,Monitor},
{Motherboard,Monitor}→{CPU},
{CPU,Monitor}→{Computer},
{Bread,Computer}→{Monitor},
{Diapers,Monitor}→{Computer},
…..
As we’ve already discussed, all these rules have the relationship with the parent rule, respectively.
“Interesting” Rules Mining
Each of these rules, produced in the previous paragraph might be more or less “interesting”, depending on a potential “strength” of the relationship between specific items in a rule’s itemset. In this paragraph, we will discuss how to estimate an interest to a rule and its importance.
Formally, an itemset of each rule being produced appears to be a subset that simultaneously occurs in one or multiple transaction itemsets ($\begin{aligned}I \subseteq t_s\end{aligned}$), listed above. The very first tendency that we might reveal on the following set of transactions is that an itemset of the first rule more “frequently” occurs as a subset of particular transaction itemsets, rather than the second one. According to the association rules mining principle, there’s more probability of the first rule’s itemset to be a potential rule “candidate”.
There’re at least two main parameters that can be used for quantifying and measuring an interest to a new rule being produced, such as either “support” or “confidence” metrics. “Support” metric is the very first parameter, by using which we can determine the interest and importance of specific rule.
To compute the support metric value, we must first find the number of transaction itemsets, in which the new rule’s itemset occurs $\begin{align}count(I \subseteq t_s | t_s \in T)\end{align}$, and, then, divide this number by the overall amount of transactions |T|:
$\begin{align}supp(I) = \frac{count(I \subseteq t_s | t_s \in T)}{|T|} \in [0;1] \end{align}$
In fact, the support metric value is actually a probability with which a rule’s itemset occurs across the set of transactions T. The rules with highest value of probability are considered to be the most interesting and important, while those rules having the smallest probability values are being insignificant.
The “confidence” metric is another useful measure of a rule’s interest and importance. As we’ve already discussed before, to produce a new rule, we must merge two rules under a certain condition. The confidence is actually the probability with which two dependent rules occur in the set of transactions together. To obtain the value of confidence, we must first find the support value for the first rule $\begin{aligned}supp(I^{'})\end{aligned} $ and for the second one $\begin{aligned}supp(I^{''})\end{aligned} $, subsequently. After that, we must divide the support value for the first rule by the value of support for the second rule:
$\begin{align}conf(I) = \frac{supp(I^{'})}{supp(I^{''})} = \frac{count(I^{'})}{count(I^{''})} \in [0;1] \end{align}$
The using of confidence metric instead of support provides more flexible interest computations, rather than the support metric, itself. Compared to the support metric, the measure of confidence allows to survive a so-called “rare item problem” by eliminating the case in which the support value is insignificant since the interesting and important rules occasionally have a low occurrence frequency.
Further, during the Apriori algorithm discussion, we will find out how to use these formulas listed above to mine the interesting and meaningful rules.
Anti-Monotonicity Principle
Both support and confidence metrics, discussed in the previous paragraph, satisfy the “downward closure lemma”, which means that the following support and confidence values for a given itemset must not exceed the minima value of support and confidence of all its subsets, respectively. That’s actually why, according to the anti-monotonicity property, the all possible subsets of an interesting rule itemset are considered to be the interesting rules. In the other words, if an itemset is frequent then all its subsets are also frequent. For example: if two rules are interesting, then the new rule produced is also interesting. Since we’ve already discussed about the association rules, it’s time to discuss about the specific algorithm that allows us to quickly and reliably perform the association rules learning (ARL) on typically huge datasets of transactions.
Apriori Algorithm
In this paragraph, we will introduce and formulate Apriori algorithm that allows us to perform scalable optimized association rules learning. Before we begin, let’s take a closer look at the association rules finding process performed by using a classical brute-force algorithm. According to the brute-force algorithm and lattice structure of data, we must generate all possible itemsets of length from 2 to N, based on the typically large 1-itemset I, containing all items extracted from an itemset $\begin{align}t_s\end{align}$ of each transaction in T. N – is the maxima length of a rule being produced. This value is normally equal to the overall amount of items in I. Initially, we consider each of these k-itemsets to be a potential rule candidate. This is a complex iterative process during each iteration of which we normally generate a multiple of (k+1)-itemsets by appending each item $\begin{align}I (\forall i_k \in I)\end{align}$ to the already existing k-itemset of the current rule, retrieved from the set. The following process starts at the rule, which 1-itemset is containing only one item, having the maxima occurrence frequency. During this process, we merge the initial rule 1-itemset with each item in I to obtain a set of 2-itemset rules. After that, we need to append each item in I to all subsequent 2-itemsets to obtain a number of 3-itemset rules, and so on, until we’ve finally ended up with an enormously huge set of rule candidates. Since we’ve generated the resultant set of rule candidates, we must compute the values of support and confidence for each rule candidate, and, then filter out only those rule candidates, which support value is greater than the value of minima support ($\begin{align}supp(I)>min\_supp\end{align}$), and the value of confidence is greater than the minima value of confidence ($\begin{align}conf(I)>min\_conf\end{align}$). For typically huge datasets, the following process might become “wasteful”, having a large impact on the CPU and system memory usage.
The Apriori procedure formulated by Agrawal and Srikant suggests a different approach for the rule candidates generation rather than the brute-force algorithm, itself. According to the Apriori algorithm, we will basically perform a “breadth-first” search, generating new rules and computing support and confidence values solely for those candidates retrieved, for which the values of support and confidence metrics exceed the minima threshold. The following exactly conforms to anti-monotonicity principle previously discussed above. Specifically, if two rule candidates have a sufficient value of support and confidence measure, then a new rule produced has exactly the same value of these metrics or higher. The following approach allows to drastically reduce the amounts of computations and system memory consumed. At the end of rules mining process, we will basically end up with a so-called “truncated” set of new rules being generated, since we no longer need to generate all possible variants of rule candidates as we’ve already done while using the classical brute-force approach.
A pseudo-code providing a general understanding of the Apriori algorithm is listed below:
$\begin{aligned} I = \{ \forall i_n | \forall i_n \in t_s, t_s \in T \}\end{aligned}$
$\begin{aligned} R_1\leftarrow I, k\leftarrow2\end{aligned}$
$\begin{aligned} while \ R_{k-1}\neq \oslash \ do \end{aligned}$
$\begin{aligned} \quad R_k\leftarrow \{ r_i \cup \{r_j\}|(r_i,r_j) \in R_k, r_i\notin r_j \} \end{aligned}$
$\begin{aligned} \quad foreach \ transaction \ t_s \in T \ do \end{aligned}$
$\begin{aligned} \quad \quad R_t\leftarrow \{r_z | r_z\in R_k, r_z \subseteq t_s\} \end{aligned}$
$\begin{aligned} \quad R_k\leftarrow \{r_s|r_s \in R_t, conf(r_s) > min\_conf\} \end{aligned}$
$\begin{aligned} \quad k \leftarrow k + 1 \end{aligned}$
$\begin{aligned} return \bigcup_k R_k\end{aligned}$
, where I - the initial 1-itemset containing all unique items extracted from each transaction $\begin{aligned}t_s\end{aligned}$ in T, $\begin{aligned}R_1\end{aligned}$ - the set of rules, containing all 1-itemsets to be analyzed, k - the length of itemset for each iteration, $\begin{aligned}R_k\end{aligned}$ - a set of rule candidates of size k being produced during k-th iteration, $\begin{aligned}R_t\end{aligned}$ - a subset of new rule candidates being generated that satisfies the specified condition ($\begin{aligned}\forall r_z \subseteq t_s \end{aligned}$), $\begin{aligned}r_z\end{aligned}$ - a k-itemset from $\begin{aligned}R_k\end{aligned}$ contained in the transaction $\begin{aligned}t_s\end{aligned}$, $\begin{aligned}r_s\end{aligned}$ - a k-itemset from $\begin{aligned}R_t\end{aligned}$ that satisfies the specified condition ($\begin{aligned}conf(\forall r_s) > min\_conf\end{aligned}$).
Step 1: Initialization
Initialization is the very first phase of the Apriori algorithm, during which we will create an initial large 1-itemset $\begin{aligned}R=\{ \forall i_k | \forall i_k \in t_s, t_s \in T\}\end{aligned} $ consisting of items extracted from each transaction’s itemset $\begin{aligned}t_s\end{aligned} $. To do this we must apply the following trivial algorithm. For each transaction in T, we’re traversing an itemset and for each specific item $\begin{aligned}\forall i_n\end{aligned} $ perform a simple check if this item already exists in the resultant itemset R. If not, we need to append this item to the resultant set R, so that we’ve obtained a set of unique $\begin{aligned}R = \{\forall i_n | count(\forall i_n) = 1\}\end{aligned} $, at the end of performing the specific computations. During the succeeding phase, we will use this 1-itemset R as the initial set of rules candidates.
Step 2: Generate Sets Of Potential Rule Candidates
Generating sets of rule candidates is the main phase of Apriori algorithm. In this phase, we will iteratively generate various of k-itemsets based on the already existing (k-1)-itemsets, obtained as the result of performing those previous iterations. The initial value of itemset size is k = 2. During each iteration, we will produce a set of rule candidates for each value of k from 2 to N. To do this, we need to extract already existing rules from the subset generated during the preceding iteration of size equal to (k – 1). After that, we produce specific pairs of rule candidate itemsets by performing a series of nested iterations. During each iteration, we simply combine a current (k-1)-itemset $\begin{aligned}R_i\end{aligned}$ with all succeeding (k-1)-itemsets $\begin{aligned}R_j\end{aligned}$, producing each new rule candidate. A very important optimization of the Apriori algorithm is that we no longer have a need to combine a (k-1)-itemset $\begin{aligned}R_i\end{aligned}$ with all other possible (k-1)-itemsets $\begin{aligned}R_j\end{aligned}$, since we’re not interested in the equivalent rules generation. This, in turn, allows to drastically reduce the potential size of the resultant set of rules and optimize performance.
For each pair of rules, we perform a verification if the first itemset $\begin{aligned}R_i\end{aligned}$ is not contained in the second itemset $\begin{aligned}R_j\end{aligned}$ (R_i∉R_j). If not, we’re performing a second-chance verification if the value of confidence of both itemsets exceed the minima threshold ($\begin{aligned}conf(R_i) > min\_conf\end{aligned}$,$\begin{aligned}conf(R_j) > min\_conf\end{aligned}$). If so, we merge these both (k-1)-itemsets to produce a new rule candidate. For a new rule candidate, we also compute a value of confidence. Finally, we need to append the newly produced candidates to the set of new rule candidates being generated and proceed with the next iteration to generate the set of new (k+1)-itemset rule candidates. We normally proceed with the following computation process, until we’ve finally obtained a set of new rules, which itemsets’ size is equal to N (k=N).
Notice that, in this particular case, we don’t use the value of support to determine a new rule’s interest in favor of measuring of confidence metric that allows to increase a flexibility of the mining process (For more information on this topic, see “Interesting Rules Mining” paragraph of this article).
According to the number of optimizations mentioned above, we no longer need to estimate a minima confidence threshold value. The following value is a constant and equals to min_conf=0.45, which means that we’re expecting to find new rules with the probability of interest equal to more than 45%. Also, we don’t have a need to increment the value of count for each new rule and use it during the rule interest estimation, as it was initially proposed by Agrawal and Srikant. The value of minima confidence threshold equal to 0.45 is a sample constant value for the most of existing association rules mining algorithms.
Step 3: Find Potentially Interesting and Meaningful Rules
The result of performing those computations, discussed above, is actually a resultant set of rules. At this point, our goal is to filter out those that are the most interesting and meaningful rules in the set. For that purpose, we need to perform a simple linear search to find all rules, for which the value of itemset size is the maxima. Specifically, we will traverse the resultant set of new rules, obtained during the previous step and for each rule's itemset, perform a check if the computed value of confidence exceeds the minima confidence threshold. If so, we will append such rules to the resultant set of interesting rules.
Step 4: Perform Data Classification
Data classification is the final phase of the Appriori algorithm, which is very simple. During this phase, we will find all rules in the set R, which itemset contains the class value. For that purpose, we will use the same trivial linear search as we've already done in the previous Step 3, briefly discussed above. Suppose we're given a set of classes $\begin{aligned}C=\{c_1,c_2,c_3,…,c_{m-1},c_m\}\end{aligned} $. For each class, $\begin{aligned}\forall c_q\end{aligned}$, we will perform a linear search in the rules set R to find those rules, which itemset contains the current class value. We will add each of these rules to the resultant set associated the specific class value.
Evaluation And Performance Optimization
As we've already discussed, the using of the Apriori algorithm brings more performance and efficience compared to the classical brute-force and other similar algorithms. Specifically, the initial variant of the brute-force algorithm's complexity can be estimated as $\begin{aligned}p=O(2^i * N)\end{aligned}$, where i - the number of rule candidates during each k-th iteration of the algorithm, and N - the overall number of iterations.
The Apriori algorithm proposed by Agrawal and Srikat in 1994 allows to perform the same association rules mining as the brute-force algorithm, providing a reduced complexity of just $\begin{aligned}p=O(i^2 * N)\end{aligned}$. Specifically, the following implementation of the Apriori algorithm has the following computational complexity at least:
$\begin{aligned}p=O(i^2 * N) + 2*N\end{aligned}$
As well, if you take a closer look at the C++11 code, implementing the Apriori algorithm, you will notice that some of the sequential code fragments performing new rule candidates generation might be run in parallel. For that purpose, we will use the Intel C++ 19.0 compiler and OpenMP performance library, which allows to drastically increase the performance speed-up, while executing the following code on symmetric multi-core Intel CPUs, providing the sufficent scalability of the legacy sequential code, implementing the Apriori algorithm being executed.
Using the Code
Implementation Of Apriori Algorithm
Since the Apriori algorithm basically relies on performing a series of the theory of set's operations, we've implemented a number of functions that allow us to perform union, intersect, append and other comparison operations on the pair of vectors used to store the itemset being processed. Here's a C++ code fragment implementing these functions:
The following function implements the fundamental sets union operation:
std::vector<std::string> union_vec(
const std::vector<std::string>& v1,
const std::vector<std::string>& v2)
{
std::vector<std::string> union_vector;
for (auto it = v1.begin(); it != v1.end(); it++)
if (std::find_if(v2.begin(), v2.end(), \
[&](const std::string& str) { return str == *it; }) != v2.end())
union_vector.push_back(*it);
return union_vector;
}
The function that performs the intersect operation is mainly based on executing the union_vec function listed above:
std::vector<std::string> intersect_vec(
const std::vector<std::string>& v1,
const std::vector<std::string>& v2)
{
std::vector<std::string> intersect_vector;
std::vector<std::string> union_vector = union_vec(v1, v2);
std::vector<std::string> v(v1);
v.insert(v.end(), v2.begin(), v2.end());
std::sort(v.begin(), v.end());
v.erase(std::unique(v.begin(), v.end()), v.end());
for (auto it = v.begin(); it != v.end(); it++)
if (std::find_if(union_vector.begin(), union_vector.end(),
[&](const std::string& str)
{ return str == *it; }) == union_vector.end())
intersect_vector.push_back(*it);
return intersect_vector;
}
There's also another fundamental function that allows to merge two itemset vectors:
std::vector<std::string> append_vec(
const std::vector<std::string>& v1,
const std::vector<std::string>& v2)
{
std::vector<std::string> v(v1);
v.insert(v.end(), v2.begin(), v2.end());
std::sort(v.begin(), v.end());
v.erase(std::unique(v.begin(), v.end()), v.end());
return v;
}
To compare two itemset vectors and perform a check if the first vector is not contained in the second one, we must implement the specific function listed below:
bool compare_vec(
const std::vector<std::string>& v1,
const std::vector<std::string>& v2)
{
std::vector<std::string> v = v2;
std::vector<std::string> v_u = union_vec(v1, v2);
return (v_u.size() != 0) ? true : false;
}
Also, there're a couple of functions that allow to perform a verification if the first vector contains the second one and if an itemset contains a specific item:
bool contains(const std::vector<std::string>& v,
const std::string& value)
{
return std::find_if(v.begin(), v.end(),
[&](const std::string& s) { return s == value; }) != v.end();
}
bool contains_vec(const std::vector<std::string>& v1,
const std::vector<std::string>& v2)
{
bool found = false;
for (auto it = v2.begin(); it != v2.end() && !found; it++)
found = contains(v1, *it) ? true : false;
return found;
}
To extract all unique items from each transaction in the set, we've implemented the following function:
std::vector<std::string> get_items(
const std::vector<std::vector<std::string>>& T)
{
std::vector<std::string> items;
for (auto it = T.begin(); it != T.end(); it++)
items.insert(items.end(), it->begin(), it->end());
std::sort(items.begin(), items.end());
items.erase(std::unique(items.begin(), items.end()), items.end());
return items;
}
To convert an item into a single item vector, we've written the miscellaneous function as follows:
std::vector<std::string> vec1d(const std::string& str) {
return std::vector<std::string>(1, str);
}
To be able to read data on classes and transactions set, we've implemented the following functions that are used for reading the data from specific file streams:
std::vector<APR_ENTITY>
read_sl_csv_file(const std::string filename)
{
std::ifstream ifs(filename, \
std::ifstream::in | std::ifstream::ate);
std::vector<APR_ENTITY> v_ent;
std::size_t file_size = (std::size_t)ifs.tellg();
char* buf = (char*)malloc(++file_size);
ifs.seekg(ifs.beg); ifs.getline(buf, ++file_size);
APR_ENTITY apr_ent;
std::memset((void*)& apr_ent, 0x00, sizeof(APR_ENTITY));
const char* delim = ",";
char* token = std::strtok(buf, delim);
while (token != nullptr)
{
std::uint32_t ci = 0L;
char* m_value_buf = (char*)malloc(256 * sizeof(char));
if (sscanf(token, "%[^:]:%d", m_value_buf, &ci) > 0)
{
apr_ent.m_value = std::string(m_value_buf); apr_ent.m_ci = ci;
v_ent.push_back(apr_ent); token = std::strtok(nullptr, delim);
}
}
free(buf); ifs.close();
return v_ent;
}
std::vector<std::vector<std::string>> \
read_data_from_csv_file(const std::string filename)
{
std::vector<std::vector<std::string>> trans_v;
std::ifstream ifs(filename, std::ifstream::in);
char* buf = (char*)malloc(sizeof(char) * 4096);
while (ifs.eof() == false && ifs.peek() >= 0)
{
std::vector<std::string> tokens_v;
const char* delim = ","; ifs.getline(buf, 4096);
char* token = std::strtok(buf, delim);
while (token != nullptr)
{
tokens_v.push_back(std::string(token));
token = std::strtok(nullptr, delim);
}
trans_v.push_back(tokens_v);
}
free(buf); ifs.close();
return trans_v;
}
Before performing the association rules mining, we must initialize the data model by implementing the following functions:
void init(const std::vector<std::string>& items,
std::vector<ASSOC_R_CAND>& R)
{
ASSOC_R_CAND asr_item;
std::memset((void*)& asr_item, 0x00, sizeof(ASSOC_R_CAND));
for (auto it = items.begin(); it != items.end(); it++) {
asr_item.m_conf = .0f;
asr_item.m_itemset = utils::vec1d(*it);
R.push_back(asr_item);
}
}
std::double_t get_conf_rule(
const std::vector<std::vector<std::string>>& T,
std::vector<std::string>& rule)
{
std::double_t count = 0L;
for (auto tran_it = T.begin(); tran_it != T.end(); tran_it++)
if (utils::union_vec(*tran_it, rule).size() == rule.size())
count++;
return count;
}
void get_conf(
const std::vector<std::vector<std::string>>& T,
std::vector<ASSOC_R_CAND>& R)
{
std::double_t count = 0L;
for (auto asr_it = R.begin(); asr_it != R.end(); asr_it++)
if ((count = get_conf_rule(T, asr_it->m_itemset)) > 0)
asr_it->m_conf = count / (std::double_t)T.size();
}
Also, to have an ability to operate the rule itemsets, we must also implement the number of helper functions that allow us to perform a search to find those rules which itemset satisfies a specific condition:
template<typename Predicate>
std::vector<ASSOC_R_CAND> find_rules(std::vector<ASSOC_R_CAND>& R, Predicate pred)
{
auto it = R.begin(); std::vector<ASSOC_R_CAND> ret_v;
while ((it = std::find_if(it, R.end(), pred)) != R.end())
ret_v.push_back(*it++);
return ret_v;
}
bool contains_rule(const std::vector<ASSOC_R_CAND>& R,
std::vector<std::string>& rule)
{
bool found = false;
auto asr_it = R.begin();
while (asr_it != R.end() && !found)
found = utils::union_vec((asr_it++)->m_itemset,
rule).size() == rule.size() ? true : false;
return found;
}
The implementation of the function performing association rules learning based on the Apriori algorithm is listed below:
std::vector<APR_RULE> \
apriori(const std::vector<APR_ENTITY>& C,
const std::vector<std::vector<std::string>>& T, bool thorough = false)
{
omp_lock_t s_lock;
omp_init_lock(&s_lock);
std::vector<std::string> \
items = utils::get_items(T);
std::string rooted = C[0].m_value;
std::vector<ARL::ASSOC_R_CAND> rules_cand_v;
ARL::init(items, rules_cand_v); ARL::get_conf(T, rules_cand_v);
for (std::uint64_t k = 2; k <= items.size(); k++)
{
std::vector<ARL::ASSOC_R_CAND> k_rule_cand_v = \
ARL::find_rules(rules_cand_v, \
[&](const ARL::ASSOC_R_CAND asr) { \
return asr.m_itemset.size() == (k - 1); });
std::vector<ARL::ASSOC_R_CAND> rules_cand_new_v;
std::size_t k_rule_cand_v_size = k_rule_cand_v.size();
#pragma omp parallel for collapse(2) schedule(guided, 4)
for (std::uint64_t i = 0; i < k_rule_cand_v_size; i++)
for (std::uint64_t j = 0; j < k_rule_cand_v_size; j++)
{
if (j <= i) continue;
if ((utils::contains(k_rule_cand_v[i].m_itemset, rooted)) ||
(utils::contains(k_rule_cand_v[j].m_itemset, rooted))) continue;
if ((k_rule_cand_v[i].m_conf > min_conf) &&
(k_rule_cand_v[j].m_conf > min_conf) || ((k - 1) <= 2))
{
#pragma omp task
{
if ((!utils::compare_vec(k_rule_cand_v[i].m_itemset,
k_rule_cand_v[j].m_itemset)) || ((k - 1) <= 2))
{
ARL::ASSOC_R_CAND asr_rule;
asr_rule.m_itemset = utils::append_vec(\
k_rule_cand_v[i].m_itemset,
k_rule_cand_v[j].m_itemset);
std::double_t rule_supp = \
ARL::get_conf_rule(T, k_rule_cand_v[i].m_itemset);
std::double_t rule_new_supp = \
ARL::get_conf_rule(T, asr_rule.m_itemset);
asr_rule.m_conf = rule_new_supp / rule_supp;
omp_set_lock(&s_lock);
if ((!ARL::contains_rule(rules_cand_new_v, \
asr_rule.m_itemset)) && (asr_rule.m_conf > min_conf))
rules_cand_new_v.push_back(asr_rule);
omp_unset_lock(&s_lock);
}
}
}
}
rules_cand_v.insert(rules_cand_v.end(), \
rules_cand_new_v.begin(), rules_cand_new_v.end());
}
std::vector<APR_RULE> output_v;
#pragma omp parallel for schedule(dynamic, 4)
for (auto c_it = C.begin() + 1; c_it != C.end(); c_it++)
{
std::vector<ARL::ASSOC_R_CAND> rules_assoc_v = \
ARL::find_rules(rules_cand_v, [&](const ARL::ASSOC_R_CAND& asr) { \
return asr.m_conf > min_conf && \
utils::contains(asr.m_itemset, c_it->m_value);
});
if (rules_assoc_v.size() > 0)
{
std::vector<std::string> \
merged(rules_assoc_v.begin()->m_itemset);
#pragma omp parallel for schedule(dynamic, 4)
for (auto rl_it = rules_assoc_v.begin() + 1;
rl_it != rules_assoc_v.end(); rl_it++)
merged = utils::append_vec(merged, rl_it->m_itemset);
APR_RULE apr_rule;
std::memset((void*)& apr_rule, 0x00, sizeof(APR_RULE));
apr_rule.m_cs = std::string(c_it->m_value);
apr_rule.m_itemset = std::vector<std::string>(merged);
apr_rule.m_itemset.erase(std::remove_if(\
apr_rule.m_itemset.begin(), apr_rule.m_itemset.end(), \
[&](const std::string s) { return s == c_it->m_value; }));
output_v.push_back(apr_rule);
}
}
return output_v;
}
}
Apriori Transactions Dataset Generator
To have an ability to evaluate the implementation of the Apriori algorithm, discussed in this article, we must also implement a C++11 code that allows to generate various transactions datasets for testimony purposes.
Here's a fragment of code implementing the datasets generator functions:
std::vector<APR_ENTITY>
read_sl_csv_file(const std::string filename)
{
std::ifstream ifs(filename, \
std::ifstream::in | std::ifstream::ate);
std::vector<APR_ENTITY> v_ent;
std::size_t file_size = (std::size_t)ifs.tellg();
char* buf = (char*)malloc(++file_size);
ifs.seekg(ifs.beg); ifs.getline(buf, ++file_size);
APR_ENTITY apr_ent;
std::memset((void*)& apr_ent, 0x00, sizeof(APR_ENTITY));
const char* delim = ",";
char* token = std::strtok(buf, delim);
while (token != nullptr)
{
std::uint32_t ci = 0L;
char* m_value_buf = (char*)malloc(256 * sizeof(char));
if (sscanf(token, "%[^:]:%d", m_value_buf, &ci) > 0)
{
apr_ent.m_value = std::string(m_value_buf); apr_ent.m_ci = ci;
v_ent.push_back(apr_ent); token = std::strtok(nullptr, delim);
}
}
free(buf); ifs.close();
return v_ent;
}
std::vector<std::double_t> \
get_classes_dist(const std::uint64_t c_max_count)
{
std::double_t cr_start = 0, \
cr_end = cr_start + 1;
std::vector<std::double_t> r_vals;
std::int64_t count = c_max_count;
while (--count >= 0)
{
std::uniform_real_distribution<
std::double_t> c_dice(cr_start, cr_end);
std::double_t value = c_dice(g_mersenne);
r_vals.push_back(((count > 0) ? \
(value - cr_start) : (1 - cr_start)));
cr_start = value; cr_end = \
cr_start + (1 - value) / (std::double_t)count;
}
return r_vals;
}
void apriori_gen(const std::uint64_t g_t_size,
const std::string cs_filename,
const std::string ent_filename,
const std::string out_filename)
{
std::ofstream ofs(out_filename, std::ofstream::out);
std::vector<APR_ENTITY> classes = \
read_sl_csv_file(cs_filename);
std::vector<APR_ENTITY> entities = \
read_sl_csv_file(ent_filename);
const std::uint64_t t_length_max = entities.size();
const std::uint64_t c_max_count = classes.size() - 2;
std::int64_t count = g_t_size - 1;
while (count >= 0)
{
std::vector<std::string> trans_v;
std::uniform_int_distribution<
std::uint64_t> tl_dice(2, t_length_max);
std::uint64_t c_size = c_max_count;
std::uint64_t t_size = tl_dice(g_mersenne);
std::vector<std::double_t> cr_ratio_v = \
get_classes_dist(c_size);
std::sort(cr_ratio_v.begin(), cr_ratio_v.end(),
[&](std::double_t v1, std::double_t v2) { return v1 > v2; });
std::uniform_int_distribution<
std::uint64_t> cr_dice(0, classes.size() - 1);
std::vector<std::uint64_t> cs_v;
for (std::uint64_t i = 0; i < c_size; i++)
{
std::uint64_t ci = 0L;
do {
ci = (classes.begin() + cr_dice(g_mersenne))->m_ci;
} while ((std::find(cs_v.begin(), cs_v.end(), ci) != cs_v.end()));
cs_v.push_back(ci);
}
trans_v.push_back((classes.begin() + cs_v[0])->m_value);
for (std::uint64_t i = 0; i < c_size; i++)
{
std::vector<APR_ENTITY> ent_v;
auto ent_it = entities.begin();
while ((ent_it = std::find_if(ent_it, entities.end(),
[&](const APR_ENTITY& apr_ent)
{ return apr_ent.m_ci == cs_v[i]; })) != entities.end())
ent_v.push_back(*(ent_it++));
std::uint64_t cr_size = \
((std::uint64_t)std::ceil(ent_v.size() * cr_ratio_v[i]));
std::uniform_int_distribution<
std::uint64_t> cr_dice(0, ent_v.size() - 1);
std::int64_t cr_count = cr_size;
while (--cr_count >= 0)
{
std::string value = "\0";
do {
value = (ent_v.begin() + \
cr_dice(g_mersenne))->m_value;
} while (std::find(trans_v.begin(),
trans_v.end(), value) != trans_v.end());
trans_v.push_back(value);
}
}
auto c_it = std::find_if(classes.begin(), classes.end(),
[&](const APR_ENTITY& apr_ent) { return apr_ent.m_ci == 0; });
if (std::find_if(trans_v.begin(), trans_v.end(),
[&](const std::string& s) {
return s == c_it->m_value; }) == trans_v.end())
trans_v.push_back(c_it->m_value);
if (trans_v.size() > 2)
{
std::string transaction = "\0"; count--;
for (auto it = trans_v.begin(); it != trans_v.end(); it++)
transaction += *it + ((it == trans_v.end() - 1) ?
((count != -1) ? '\n' : '\0') : ',');
std::size_t ts_length = transaction.length();
ofs.write(transaction.c_str(), (count != -1) ? ts_length : ts_length - 1);
}
}
ofs.close();
}
Points of Interest
For a long time, I've been seeking an algorithm that allows to perform a data classification, providing better results rather than using k-means clustering and naive Bayessian classifier, commonly used. Finally, I've read a series of articles, in which authors introduced the association rules learning concepts for using it to classify the various of data, including the either classical brute-force or the scalable optimized Apriori algorithms that can be used for association rules mining. Finally, I was so impressed that the process for association rules learning and performing the classification based on the following process has never been that simple, compared to using of ANNs and other AI machine learning algorithms. The Apriori algorithm is also "ideal" for performing data classification and arranging these data into hierarchical data structures, such as building various of class taxonomies from the data obtained from dynamic streams in near real-time.
History
- 3rd July, 2019 - Published first revision of this article
