The audience of this article's readers will find out how to perform association rules learning (ARL) by using FPGrowth algorithm, that serves as an alternative to the famous Apriori and ECLAT algorithms.
Table of Contents
Introduction
In the previous article, Association Rules Learning (ARL): Part 1 - Apriori Algorithm, we’ve discussed about Apriori algorithm that allows to quickly and efficiently perform association rules mining, based on the process of finding statistical trends and insights, such as the probability with which specific items occur in a given transactions set, as well as the other patterns exhibited on the data obtained from one or multiple of streams, collecting data in near real-time.
Specifically, the association rules mining by using Apriori algorithm solely relies on the process of populating a large amounts of new rule candidates, produced based on the sets of already existing rules, and determining an “interest” to each new rule by using various of metrics, such as either a “support” or “confidence”. Obviously, that, the process of new rule candidate generation is a complex computational task, since the amounts of operations performed exponentially grows as the potential size of a dataset is proportionally increasing. Moreover, according the Apriori algorithm, the new association rules are mined based on the sets of particular items, rather than sets of transactions. Typically, sets of items have a larger size compared to sets of transactions, itself. This makes the association rules mining process to consume more CPU’s and system memory resources. The following is the main disadvantage of both Apriori and ECLAT association rules learning algorithms.
In fact, the Apriori and ECLAT algorithms, initially proposed by Agrawal and Srikant, compared to the classical brute-force algorithm, allow to reduce the computational complexity of association rules mining process to only \(\begin{aligned}O(|i|^2)\end{aligned}\), where \(\begin{aligned}|i|\end{aligned}\) - the overall number of unique items across all transactions in a set.
To perform an efficient association rules mining in the potentially huge datasets, we need a different algorithm, rather than those algorithms, mentioned above.
FPGrowth – (Frequent Patterns Growth) is another alternative to the famous Apriori and ECLAT algorithms, providing even more reduced computational complexity of the association rules mining process. According to FPGrowth algorithm, we no longer need to generate sets of new rule candidates by iterating through a given dataset k – times. Instead, we will construct a compacted hierarchical data structure, called “FP-Tree”, and, then, extract frequent itemsets from the FP-Tree directly based on the “divide and conquer” approach by performing a trivial “depth-first” search.
The main benefit of using FP-Tree data structure is that it preserves the entire data used for frequent patterns mining, never performing any modifications of the existing data, as well as never truncating long patterns for any transactions. Also, FPGrowth allows to eliminate the least frequent items and itemsets by filtering out only those the most frequent patterns from the FP-Tree. All patterns in the FP-Tree are arranged in the frequency descending order, that allows to drastically reduce the complexity of the frequent patterns extraction process.
Due to the number of optimizations mentioned above, FPGrowth algorithm provides the full computational complexity of the associate mining process that can be estimated as \(\begin{aligned}p≤O(2*|T|^2+|T|)≤O(|i|^2)\end{aligned}\), where \(\begin{aligned}|T|\end{aligned}\) – the overall amount of transactions being processed. This is the overall complexity of two algorithm’s phases, such as either building the FP-Tree \(\begin{aligned}O(2*|T|^2 )\end{aligned}\) or performing frequent patterns mining \(\begin{aligned}O(|T|)\end{aligned}\). Notice that, the overall amount of transactions \(\begin{aligned}|T|\end{aligned}\) is typically much less than the amount of particular items \(\begin{aligned}|i|\end{aligned}\) being processed \(\begin{aligned}|T|≪|i|\end{aligned}\)
However, the FPGrowth algorithm is oriented for using it to perform association rules mining, analyzing data stored in a database, rather than the data obtained from real-time data streams. As a workaround to the following issue, we will discuss how to transform a real-time data stream into a canonical database that can be used as an input dataset for the association rules mining process, formulated as FPGrowth algorithm.
In this article, we will formulate the original FPGrowth algorithm and discuss about its implementation by using C++11 programming language.
Background
Convert Real-Time Data Stream to a Canonical Database
To have an ability to perform association rules mining in the data using FPGrowth algorithm, first we must transform a real-time data stream into a canonical database, as follows:
Suppose we’re given a set of transactions \(\begin{aligned}T={t_1,t_2,t_3,...,t_(n-1),t_n }\end{aligned}\), obtained from a real-time data stream:
| TID | Transaction |
| 1 | Engine, Vehicle, Steering, CPU, Brakes, Motherboard, Machines, Appliances |
| 2 | CPU, Wheels, Tank, Motherboard, Seats, Camera, Cooler, Computer, Machines, Appliances |
| 3 | Motherboard, Steering, Monitor, Brakes, Engine, Vehicle, Machines, Appliances |
| 4 | CPU, Steering, Brakes, Cooler, Monitor, GPU, Computer, Machines, Appliances |
| 5 | Vehicle, Cooler, CPU, Steering, Brakes, Wheels, Tank, Engine, Machines, Appliances |
| 6 | Computer, CPU, Motherboard, GPU, Cooler, Engine, Machines, Appliances |
| 7 | Brakes, Vehicle, Tank, Engine, CPU, Steering, Machines, Appliances |
| 8 | Pens, Ink, Pencils, Desk, Typewriter, Brushes, Office, Appliances |
| 9 | Ink, Typewriter, Pencils, Desk, Office, Appliances |
And a set of pre-defined classes \(\begin{aligned}C={c_1,c_2,c_3,…,c_(m-1),c_m}\end{aligned}\), listed below:
| ID | Class |
| 1 | Appliances |
| 2 | Machines |
| 3 | Vehicle |
| 4 | Computer |
| 5 | Office |
The entire set of transactions must be converted into a canonical database, having the following format:
| TID | Transaction |
| 1 | Appliances, Machines, Vehicle, CPU, Brakes, Engine, Motherboard, Steering
|
| 2 | Appliances, Machines, Computer, CPU, Motherboard, Cooler, GPU, Tank, Wheels, Camera, Seats |
| 3 | Appliances, Machines, Vehicle, Brakes, Engine, Motherboard, Steering, Monitor |
| 4 | Appliances, Machines, Computer, CPU, Brakes, Motherboard, Steering, Cooler, GPU, Monitor |
| 5 | Appliances, Machines, Vehicle, CPU, Brakes, Engine, Steering, Cooler, Tank, Wheels |
| 6 | Appliances, Machines, Computer, CPU, Engine, Motherboard, Cooler, GPU |
| 7 | Appliances, Machines, Vehicle, CPU, Brakes, Engine, Steering, Tank |
| 8 | Appliances, Office, Desk, Ink, Pencils, Typewriter, Brushes, Pens |
| 9 | Appliances, Office, Desk, Ink, Pencils, Typewriter |
As you can see from the chart above, a canonical database is much similar to the “raw” data stream with only one difference that particular items in the itemset of each transaction are actually sorted in the descending order by their occurrence frequency. In this case, the occurrence frequency is estimated as the number of times a particular item occurs in the following set of transactions.
To perform the following transformation, we must use an algorithm formulated as follows:
- Find a set of items, appearing in the itemset of each transaction \(\begin{aligned}I=\{\forall i_k | i_k \in t_s, t_s \in T\};\end{aligned}\)
- Compute the occurrence frequency for each item \(\begin{aligned}\forall i_k\end{aligned}\) in the itemset \(\begin{aligned}I=\{(\forall i_k,count(\forall i_k )) | i_k \in t_s,t_s \in T\};\end{aligned}\)
- Sort all items \(\begin{aligned}\forall i_k \in I\end{aligned}\) by their occurrence frequency in the descending order;
- For each “class” \(\begin{aligned}\forall c_j \in C\end{aligned}\), find all items in \(\begin{aligned}I\end{aligned}\), representing the “class” and add them to the itemset \(\begin{aligned}I_c=\{(\forall i_k,count(\forall i_k )) | i_k=c_j,c_j \in C\};\end{aligned}\)
- Prune all items in \(\begin{aligned}I\end{aligned}\), representing a “class” \(\begin{aligned}\forall i_k \in I_c \in I;\end{aligned}\)
- Sort all items representing a “class” \(\begin{aligned}\forall i_k \in I_c\end{aligned}\) by the occurrence frequency in the descending order;
- Append the itemset \(\begin{aligned}I_c\end{aligned}\), containing classes to the top of itemset \(\begin{aligned}I (I \leftarrow I_c);\end{aligned}\)
- For each transaction \(\begin{aligned}t_s \in T\end{aligned}\) itemset arrange all items by the frequency descending order in \(\begin{aligned}I\end{aligned}\);
According to the following algorithm listed above, we first have to find an itemset I, containing all items retrieved from the itemset of each transaction \(\begin{aligned}t_s \in T\end{aligned}\). Unlike Apriori algorithm, we need to retrieve not only “unique”, but also those items that occur in more than one transaction itemset and after that, compute the occurrence frequency in T for each specific item being retrieved. At the end of performing the specific computations, the itemset I will contain pairs of “item - count” values. During the algorithm discussion, we will consider the following occurrence frequency will represent a “support” count metric for each of those items. Finally, we have to sort the itemset I by the support count in the descending order. For example: According to the following algorithm listed above, we first have to find an itemset I, containing all items retrieved from the itemset of each transaction \(\begin{aligned}t_s \in T\end{aligned}\). Unlike Apriori algorithm, we need to retrieve not only “unique”, but also those items that occur in more than one transaction itemset and after that, compute the occurrence frequency in T for each specific item being retrieved. At the end of performing the specific computations, the itemset I will contain pairs of “item - count” values. During the algorithm discussion, we will consider the following occurrence frequency will represent a “support” count metric for each of those items. Finally, we have to sort the itemset I by the support count in the descending order. For example:
| TID | Transaction |
| 1 | Engine, Vehicle, Machines, Appliances |
| 2 | CPU, Motherboard, Seats, Computer, Machines, Appliances |
| 3 | Steering, Brakes, Engine, Vehicle, Machines, Appliances, Motherboard |
| 4 | CPU, Cooler, Monitor, GPU, Computer, Machines, Appliances, Steering |
| 5 | Typewriter, Office, Pencils |
| … | … |
| ID | Item | Support Count |
| 1 | Appliances | 4 |
| 2 | Machines | 4 |
| 3 | Vehicle | 2 |
| 4 | Computer | 2 |
| 5 | Office | 1 |
| 5 | Engine | 2 |
| 6 | CPU | 2 |
| 7 | Seats | 1 |
| 8 | Steering | 2 |
| 9 | Brakes | 1 |
| 10 | Cooler | 1 |
| 11 | Monitor | 1 |
| 12 | GPU | 1 |
| 13 | Motherboard | 2 |
| 14 | Typewriter | 1 |
| 15 | Pencils | 1 |
To obtain the itemset illustrated in the chart above, we must iterate through the itemset of classes C and for each class, find all occurrences of the current class \(\begin{aligned}(\forall i_k,count(\forall i_k )) | \forall i_k=c_j\end{aligned}\) in the itemset \(\begin{aligned}I\end{aligned}\). Then, we have to add each class occurrence to the itemset \(\begin{aligned}I_c\end{aligned}\) and remove each of the occurrences \(\begin{aligned}\forall i_k \in I_c \in I\end{aligned}\) from the itemset \(\begin{aligned}I\end{aligned}\). Also, we must sort the new itemset \(\begin{aligned}I_c\end{aligned}\) in the occurrence frequency descending order.
Since we’ve filtered out all classes from the itemset \(\begin{aligned}I\end{aligned}\), now we can simply merge these two itemsets \(\begin{aligned}I\end{aligned}\) and \(\begin{aligned}I_c\end{aligned}\) by appending the itemset \(\begin{aligned}I_c\end{aligned}\) to the top of the itemset \(\begin{aligned}I\end{aligned}\). This is typically done to prioritize those items representing a class, that must appear in each transaction itemset \(\begin{aligned}t_s\end{aligned}\) first.
The data stream conversion process is actually a multi-dimensional task. The performing of the following task normally leads to obtaining a variety of datasets, in which items are arranged in their specific order. Since we’re interested to obtain the only one resultant dataset shown below, we have defined a set of classes C, in order to reduce the dimensionality of the following task and thus make the following process more finite.
Finally, we have to iterate through the set of transactions \(\begin{aligned}T\end{aligned}\), and for each transaction \(\begin{aligned}t_s\end{aligned}\), we must re-arrange items within its itemset by sorting them in the frequency descending order, exactly matching the order of items in \(\begin{aligned}I\end{aligned}\). To do that, we iterate the itemset \(\begin{aligned}I\end{aligned}\) and for each item perform a linear search to find a position of the following item \(\begin{aligned}\forall i_k\end{aligned}\) in the current transaction \(\begin{aligned}t_s\end{aligned}\). Since the position value is found, we must exchange the item in the following position with the item located in the next position from the beginning of the transaction itemset. The following computation is performed for each transaction\(\begin{aligned}t_s \in T\end{aligned}\). As the result of performing those computations, we will obtain the following canonical database of transactions:
| TID | Transaction |
| 1 | Appliances, Machines, Vehicle, Engine, Seats |
| 2 | Appliances, Machines, Computer, CPU, Motherboard, Seats |
| 3 | Appliances, Machines, Vehicle, Engine, Steering, Motherboard, Brakes |
| 4 | Appliances, Machines, Computer, CPU, Steering, Cooler, Monitor |
| 5 | Office, Typewriter, Pencils |
| … | … |
FPGrowth Algorithm
In this paragraph, we will briefly introduce one of the variants of FP-Growth algorithm and thoroughly discuss about some of its phases and characteristics. As we’ve already discussed before, FPGrowth algorithm serves as an alternative to the famous Apriori and ECLAT algorithm, providing more efficiency to the process of association rules mining.
Instead of performing the breadth-first traversal to produce all possible variants of association rule candidates, the following algorithm allows to build a compacted data structure called FP-Tree and extract the most interesting and meaningful association rules directly from the tree, making the entire process of rules mining somewhat smarter. The entire process of association rules mining formulated as FPGrowth algorithm is basically performed in two main phases:
- Build a compacted hierarchical data structure, called FP-Tree;
- Extract the interesting association rules, directly, from the tree;
During the first phase, we will construct the specific FP-Tree based on the data stored in a given set of transactions. The main purpose of the following phase is to reveal all most frequent patterns exhibited on the transactional data, and, obviously, build an FP-Tree, representing the relations of particular items to the most frequent patterns, mined. We consider a “pattern” to be a particular subset of items that the most frequently appear in the given set of transactions. Similar to the other algorithms, FPGrowth solely relies on the hypothesis that items occurring along with the most frequent patterns in the dataset are also the most frequent, according to the anti-monotonicity principle. The combinations of specific frequent patterns and other items pretend to be the candidates for the most interesting association rules.
During the following process, we will actually filter out all the most frequent patterns from a specific set of transactions and map them to a specific path on the FP-Tree, so that at the end of this process, all the most frequent patterns are positioned closely to the root of the tree. According to the FP-Tree building algorithm, these frequent pattern nodes are interconnected with the rest of other items, which are the “leaves” of the FP-Tree.
As you’ve might already known, the most evident issue of the entire class of association rules mining algorithms is the potential “lack” of information used for the decision-making process, while performing the association rules mining. That’s actually why, we normally need to extend the existing FP-Tree built with cross-references, interconnecting specific similar items, which makes the following computational process more flexible. Also, we use a set of pre-defined classes to reduce the dimensionality of this process, making it faster and more finite. In fact, the FP-Tree built is actually a variant of decision-making trees used specifically for association rules mining.
We consider the FP-Tree built to be a compacted data structure, since we never expand the horizontal width of the following tree, which might cause the unpredictable results of mining. Instead, we “grow” the height of the following tree making it vertically “tall”, so that, at the end of performing this process, we obtain a complete FP-Tree that can be reliably used for extracting the most interesting associations from the tree directly.
As well as the other algorithms, FPGrowth is mainly based on each pattern support count estimation. Specifically, we extract only those patterns which support count exceeds a specific threshold sample value. Unlike Apriori and ECLAT, we don’t use the “confidence” or other metrics rather than “support” metric with the FPGrowth algorithm. This allows us to drastically simplify the process of interesting rules mining.
Extract the interesting association rules based on the data compacted into FP-Tree is another phase of FPGrowth, during which we will perform a trivial “depth-first” search to find all the most interesting and meaningful rules by using the support count metric. During this phase, we use a “divide and conquer” approach to perform a full traversal of the FP-Tree nodes. Unlike the conventional “depth-first” search, we perform the so-called “bottom-up” traversal starting at those nodes that represent specific classes to find all subsets, which items belong to a specific class. Finally, we merge all those subsets found into an entire set of items for a given class.
In the next paragraphs of this article, we will thoroughly discuss about all those FPGrowth algorithm phases briefly introduced above.
Step 1: Build An FP-Tree
In this paragraph, we will discuss how to build a compact data structure, called “FP-Tree”, to represent the most frequent association rule patterns hierarchically. During this process, we will basically deal with an entire set of transactions T, rather than the itemset I containing all items from the following set, discussed in the one of the previous paragraphs.
The FP-Tree is an oriented acyclic graph G=(P,E) , where P- a set of tree’s “nodes”, each one representing a specific “prefix” or “item”, and E- a set of “edges” joining particular “nodes” into a hierarchical tree. Those “nodes” that don’t have of “child” nodes are called “leaves” and represent particular “items” associated with specific “prefixes”.
To find out what particularly those prefixes are, let’s take a closer look at the set of transactions shown above. A “prefix” is a subset of items that overlaps in more than one transaction itemset from the beginning of an itemset.
For example, transactions t_1={"Appliances","Machines","Vehicle","Engine","Seats"} and t_3={"Appliances","Machines","Vehicle","Engine","Steering","Motherboard","Brakes"} have an overlapped subset of {"Appliances","Machines","Vehicle","Engine"}, which is considered to be a common “prefix” of these two transaction itemsets.
During the discussion, we will demonstrate how to build an “FP-Tree” that can be represented as a set of nodes, each one referencing a “parent” and multiple of “adjacent” nodes. To build the tree, we actually must retrieve all prefixes from the set of transactions T by using the following algorithm.
Initialization
First, what we have to do is to initialize the FP-Tree being constructed. To do that, we must add an initial “rooted” node to the set. The following node, unlike the other nodes that will be added, initially has no references to either a “parent” or “adjacent” nodes.
After that, we need to retrieve the first transaction from t_1 from the set T, and append each item to the tree, one-by-one, respectively, starting at the “rooted” node, previously added. It means that for each item in the transaction t_1 we will add a specific node to the tree, referencing the either a previous item node (i.e., “parent”) or a set of the succeeding item nodes (i.e., “adjacent”). Also, each new node added to the tree will have a specific value of support count. Initially, the value of support count for each new node is equal to 0.
In this case, each node in the tree will have only one adjacent, representing the succeeding item node. Also, we must create a separate set of prefixes P', in which we will store each prefix obtained as the result of adding specific item nodes to the tree, as shown in the chart below. In this case, the following prefix is associated an index of the specific node in set P. Each prefix in P' is built as the result of performing a concatenation of each next item to all previous ones, as it's shown in the chart below. The node index, in this particular case, actually represents the index of the last item of the current prefix. Also, we have to make sure that the set of prefixes P' has no duplicates. The duplicate prefixes are simply pruned.
The following operation is equivalent to creating a doubly linked list of items. As the result of performing the following operation, we will obtain the following tree:
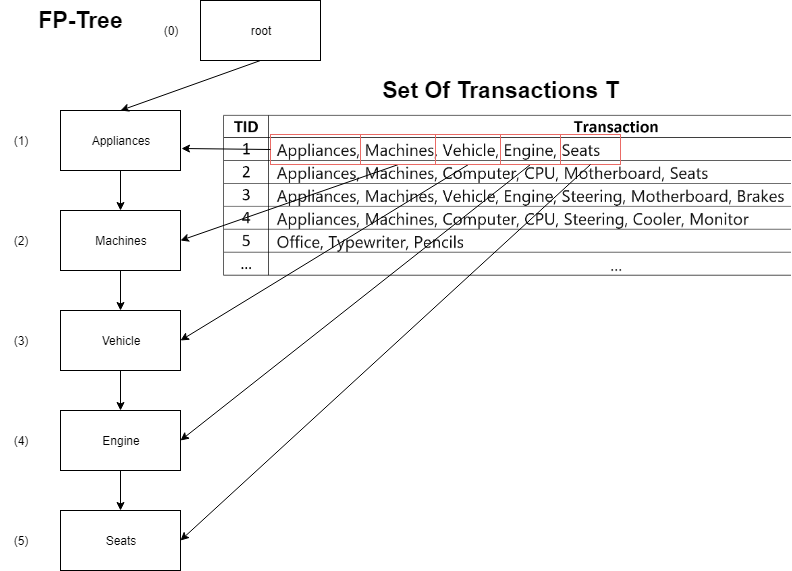
| ID | Prefixes | Item ID |
| 1 | Appliances | 1 |
| 2 | Appliances, Machines | 2 |
| 3 | Appliances, Machines, Vehicle | 3 |
| 4 | Appliances, Machines, Vehicle, Engine | 4 |
Add New Nodes To FP-Tree
Since we’ve initialized the tree with the items in the first transaction, we must iterate through the set of transactions T, starting at the second transaction t_2, and for each transaction t_s∈T perform a linear search in the subset of preceding transactions to find a transaction t_k having the longest occurrence of the common prefix with t_s. If such transaction t_k is found, then we’re performing a lookup in the set of prefixes P^' to find the following prefix and obtain a specific index of the node to which all other new non-overlapped item nodes will be appended.
Finally, we add each non-overlapped node one-by-one, similarly as we’ve already done it during the initialization phase, starting at the specific prefix node. Otherwise, if no overlapped transaction t_k was found, then, we directly append new nodes to the rooted node of the tree. Also, for duplicate transaction that once have already occurred, we actually don’t need to add new nodes to the tree, but solely increment the value of support count for each already existing node, as it’s thoroughly discussed below.
How to Find Prefixes
To find prefixes of two or more transaction itemsets, we must use the following algorithm. Suppose we’re having two transaction itemsets, t_s and t_k . To find a prefix (if exists), we must iterate through each item in t_s and t_k and perform a check if the current item in t_s is equal to the current item in t_k. If so, we must enqueue the current item in t_s in a separate prefix itemset and proceed with the next pair of items, otherwise terminate the procedure.
At the end of performing this operation, the prefix itemset will contain all items that overlap (i.e., exist) in both t_s and t_k itemsets. The following subset of items being retrieved is considered to be the prefix of these both itemsets. This operation is much like the finding a union of two itemsets t_s∪t_k with only one difference that we must preserve the sequence and orientation, in which the overlapped items exists in both itemsets. Specifically, we’re finding a union of two itemsets starting at the beginning of each itemset, so that the items in t_s must match the order of equal items in t_k (t_s⨃t_k).
Accumulate Support Counts
For each overlapped item node, we also must increment the value of support count by 1, by iterating over each overlapped item node starting at the last one to the root node of the tree. For example, if the support count for those overlapped item nodes “Appliances” and “Machines” was equal to 1, then after performing the following computation, the support count of each of these items will be increased to 2, whilst the support count of the rest of all non-overlapped items, such as Vehicle, Engine, Computer, CPU, … , will be equal to 1. We must update the data model being constructed, so that at the end of performing those computations, each node of the complete FP-Tree will be associated with a proper value of its support count.
Cross-References
As you’ve might already noticed from the figure shown above, the FP-Tree being constructed might also contain duplicate items, for which we have a need to add bidirectional cross-references. This is typically done by iterating the set of nodes P, and for each node ∀p_i perform a linear search in the subset of succeeding nodes to find a node ∀p_j having the identical item value. If such node is found, then we add the index of this node j to the set of adjacent nodes for ∀p_i, and vice versa. In this case, as the result of performing those computations, we will obtain the following tree and a particular set of prefixes:

| ID | Prefixes | Item ID |
| 1 | Appliances | 1 |
| 2 | Appliances, Machines | 2 |
| 3 | Appliances, Machines, Vehicle | 3 |
| 4 | Appliances, Machines, Vehicle, Engine | 4 |
| 5 | Appliances, Machines, Vehicle, Engine, Seats | 5 |
| 6 | Appliances, Machines, Computer | 6 |
| 7 | Appliances, Machines, Computer, CPU | 7 |
| 8 | Appliances, Machines, Computer, CPU, Motherboard | 8 |
| 9 | Appliances, Machines, Computer, CPU, Motherboard, Seats | 9 |
| 10 | Office | 10 |
| 11 | Office, Typewriter | 11 |
| 12 | Office, Typewriter, Pencils | 12 |
Since we’ve completed the FP-Tree construction process, we will obtain the following set of nodes:
| ID | Item | Parent | Adjacent | Support Count |
| 1 | root | 0 | {2} | 0 |
| 2 | Appliances | 1 | {3} | 2 |
| 3 | Machines | 2 | {4,5} | 2 |
| 4 | Vehicle | 3 | {6} | 2 |
| 5 | Computer | 3 | {8} | 2 |
| 6 | Engine | 4 | {7,11} | 2 |
| 7 | Seats | 6,10 | {10} | 1 |
| 8 | CPU | 5 | {9,14} | 2 |
| 9 | Motherboard | 8 | {10,12} | 1 |
| 10 | Seats | 9 | {7} | 1 |
| 11 | Steering | 6 | {12,14} | 1 |
| 12 | Motherboard | 11 | {9,13} | 1 |
| 13 | Brakes | 12 | {} | 1 |
| 14 | Steering | 8 | {11,15} | 1 |
| 15 | Cooler | 14 | {16} | 1 |
| 16 | Monitor | 15 | {} | 1 |
| 17 | Office | 1 | {18} | 1 |
| 18 | Typewriter | 17 | {19} | 1 |
| 19 | Pencils | 18 | {} | 1 |
Since, we’ve finally constructed a complete FP-Tree, in the next paragraph, we will thoroughly discuss how to use the following hierarchical data structure to find the most interesting and meaningful association rules based on the data model represented as the FP-Tree, by performing a trivial “depth-first” search.
Step 2: Extract Frequent Patterns Directly From FP-Tree
Since we’ve successfully built an FP-Tree and computed support counts for each specific item from the transactions set, now it’s time to extract all possible frequent patterns from the tree to have an ability of finding those interesting and meaningful association rules, mined. For that purpose, we must iterate through the set of support counts I_s and for each specific item find a corresponding node (i.e., “leaf”) in the set P having the maxima support count value ∀p_k. After that, starting at the specific item node ∀p_k, obtained from the set of nodes P, we must find a prefix path by iterating through each parent node “bottom-up”, until we’ve finally reached the rooted node of the tree. For those nodes having more than one parent node, we select the node with largest support count value. During each iteration, we must add specific item to the set of items, representing the most frequent prefix.
Finally, since a particular most frequent prefix was found, we have to prune all infrequent items away from the following prefix itemset. To do that, we must union the following itemset with the set of classes C. At the same we must find an intersection of the union set and the prefix set obtained as the result of performing the “bottom-up” traversal. Algebraically, this can be denoted as B=A∩(A∪C), where A – the prefix itemset, C – the set of classes.
After that for each item in B, we must create a subset of items B^' based on the concatenation of current prefix A and the value of current item. Finally, we have to compute the value of the number of times the itemset B occurs in the set of transactions T, and perform a check if the following value is less than the minima support count threshold. The minima support count value is a sample constant ratio value, which for the typically huge datasets is equal to supp_count{min}=0.07, which just 7% of the entire dataset. To obtain the desired value of support count all what we have to do is to multiple the ratio by the number of transactions in the set T.
Step 3: Find Interesting and Meaningful Association Rules
After we’ve built an FP-Tree and extracted all frequent patterns (i.e., frequent prefixes), it’s time to retrieve all possible association rules. In this case, this is typically done by merging all itemsets obtained during the previous phase, discussed above. To merge all itemset obtained, we must iterate through a set of classes C, and for each class ∀c_i , find all those resultant itemsets containing the current class, and add them into a separate resultant set. After that, we simply have to find an intersection of all of those itemsets and merge them into a single set associated with the current class. Finally, since we’ve obtained a merged itemset we must add it to the resultant set, in which each class is mapped to a specific set of items, belonging to it. The algorithm’s phase discussed above is the final phase, after performing which we have no need to perform any additional data processing.
Using the Code
#include <iostream>
#include <vector>
#include <string>
#include <iterator>
#include <algorithm>
#include <fstream>
#include <omp.h>
#include <pstl algorithm="">
#include <pstl execution="">
#pragma warning(disable:2586)
std::string filename = "\0";
const std::string cs_filename = "classes.csv";
namespace utils {
std::vector<std::string> union_vec(
const std::vector<std::string>& v1,
const std::vector<std::string>& v2)
{
std::vector<std::string> union_vector;
for (auto it = v1.begin(); it != v1.end(); it++)
if (std::find_if(pstl::execution::par_unseq, v2.begin(), v2.end(), \
[&](const std::string& str) { return str == *it; }) != v2.end())
union_vector.push_back(*it);
return union_vector;
}
std::vector<std::string> intersect_vec(
const std::vector<std::string>& v1,
const std::vector<std::string>& v2)
{
std::vector<std::string> intersect_vector;
std::vector<std::string> union_vector = union_vec(v1, v2);
std::vector<std::string> v(v1);
v.insert(v.end(), v2.begin(), v2.end());
std::sort(pstl::execution::par_unseq, v.begin(), v.end());
v.erase(std::unique(pstl::execution::par_unseq, v.begin(), v.end()), v.end());
for (auto it = v.begin(); it != v.end(); it++)
if (std::find_if(pstl::execution::par_unseq,
union_vector.begin(), union_vector.end(),
[&](const std::string& str)
{ return str == *it; }) == union_vector.end())
intersect_vector.push_back(*it);
return intersect_vector;
}
std::vector<std::string> append_vec(
const std::vector<std::string>& v1,
const std::vector<std::string>& v2)
{
std::vector<std::string> v(v1);
v.insert(v.end(), v2.begin(), v2.end());
std::sort(pstl::execution::par_unseq, v.begin(), v.end());
v.erase(std::unique(pstl::execution::par_unseq, v.begin(), v.end()), v.end());
return v;
}
};
namespace ARL
{
const std::double_t min_supp = 0.06;
typedef struct tagFpTreeNode
{
std::uint64_t m_count;
std::string m_item;
std::vector<std::int64_t> m_parent;
std::vector<std::uint64_t> m_adj;
} FPTREE_NODE;
typedef struct tagFpPrefix
{
std::uint64_t m_leaf;
std::vector<std::string> m_prefix;
} FP_PREFIX;
typedef struct tagFpSuppCount
{
std::uint64_t m_count = 0L;
std::string m_item;
} FP_SUPP_COUNT;
typedef struct tagFpClassItem
{
std::string m_class;
std::vector<std::string> m_items;
} FP_CLASS_ITEM;
std::vector<std::string>
read_sl_csv_file(const std::string filename)
{
std::ifstream ifs(filename, \
std::ifstream::in | std::ifstream::ate);
std::vector<std::string> v_ent;
std::size_t file_size = (std::size_t)ifs.tellg();
char* buf = (char*)malloc(++file_size);
ifs.seekg(ifs.beg); ifs.getline(buf, ++file_size);
const char* delim = ",";
char* token = std::strtok(buf, delim);
while (token != nullptr)
{
std::uint32_t ci = 0L;
char* m_value_buf = (char*)malloc(256 * sizeof(char));
if (sscanf(token, "%[^:]:%d", m_value_buf, &ci) > 0)
{
v_ent.push_back(std::string(m_value_buf));
token = std::strtok(nullptr, delim);
}
}
free(buf); ifs.close();
return v_ent;
}
std::vector<std::vector<std::string>> \
read_data_from_csv_file(const std::string filename)
{
std::vector<std::vector<std::string>> trans_v;
std::ifstream ifs(filename, std::ifstream::in);
char* buf = (char*)malloc(sizeof(char) * 4096);
while (ifs.eof() == false && ifs.peek() >= 0)
{
std::vector<std::string> tokens_v;
const char* delim = ","; ifs.getline(buf, 4096);
char* token = std::strtok(buf, delim);
while (token != nullptr)
{
tokens_v.push_back(std::string(token));
token = std::strtok(nullptr, delim);
}
trans_v.push_back(tokens_v);
}
free(buf); ifs.close();
return trans_v;
}
std::vector<std::string> fp_get_prefix(\
std::vector<std::string>& v1, \
std::vector<std::string>& v2)
{
std::uint64_t index = 0;
std::vector<std::string> fp_prefix;
while (index < v1.size() && \
index < v2.size() && (v1[index] == v2[index]))
fp_prefix.push_back(v1[index++]);
return fp_prefix;
}
std::vector<std::string> get_items(
const std::vector<std::vector<std::string>>& T)
{
std::vector<std::string> items;
for (auto it = T.begin(); it != T.end(); it++)
items.insert(items.end(), it->begin(), it->end());
std::sort(pstl::execution::par_unseq, items.begin(), items.end());
items.erase(std::unique(pstl::execution::par_unseq,
items.begin(), items.end()), items.end());
return items;
}
std::vector<fp_supp_count> fp_get_supp_count(\
std::vector<std::string> fp_items, \
const std::vector<std::vector<std::string>>& T)
{
std::vector<fp_supp_count> fp_supp_count;
for (auto it = fp_items.begin(); it != fp_items.end(); it++)
{
std::uint64_t count = 0L;
for (auto tr_it = T.begin(); tr_it != T.end(); tr_it++)
count += std::count_if(pstl::execution::par_unseq,
tr_it->begin(), tr_it->end(),
[&](const std::string& item) { return item == *it; });
FP_SUPP_COUNT fp_supp_item;
fp_supp_item.m_count = count;
fp_supp_item.m_item = std::string(*it);
fp_supp_count.push_back(fp_supp_item);
}
std::sort(pstl::execution::par_unseq,
fp_supp_count.begin(), fp_supp_count.end(),
[&](const FP_SUPP_COUNT& item1, const FP_SUPP_COUNT& item2) {
return (item1.m_count > item2.m_count);
});
return fp_supp_count;
}
void fp_convert_stream(\
std::vector<fp_supp_count> fp_supp_counts, \
std::vector<std::vector<std::string>>& T, \
std::vector<std::string>& C)
{
std::vector<fp_supp_count> classes;
for (auto it = C.begin(); it != C.end(); it++)
{
auto c_it = std::find_if
(pstl::execution::par_unseq, fp_supp_counts.begin(), \
fp_supp_counts.end(), [&](const FP_SUPP_COUNT& fp_supp) {
return fp_supp.m_item == *it; });
if (c_it != fp_supp_counts.end())
{
classes.push_back(*c_it);
fp_supp_counts.erase(c_it);
}
}
std::sort(pstl::execution::par_unseq, classes.begin(), classes.end(),
[&](const FP_SUPP_COUNT& item1, const FP_SUPP_COUNT& item2) {
return (item1.m_count > item2.m_count);
});
fp_supp_counts.insert(fp_supp_counts.begin(), \
classes.begin(), classes.end());
for (auto it = T.begin(); it != T.end(); it++)
{
std::uint64_t cpos = 0L;
auto supp_it = fp_supp_counts.begin();
while (supp_it != fp_supp_counts.end())
{
auto item_it = std::find(pstl::execution::par_unseq, it->begin(), \
it->end(), supp_it->m_item);
if (item_it != it->end())
std::iter_swap(item_it, (it->begin() + cpos++));
supp_it++;
}
}
}
std::vector<fptree_node> fp_init_tree(\
std::string item, std::uint64_t count)
{
FPTREE_NODE node;
node.m_count = count;
node.m_parent.push_back(-1L); node.m_item = std::string(item);
return std::vector<fptree_node>(1, node);
}
std::uint64_t fp_add_node(std::vector<fptree_node>& fp_tree, \
std::uint64_t parent, std::string item, std::uint64_t count)
{
FPTREE_NODE node;
node.m_count = count;
node.m_parent.push_back(parent); node.m_item = std::string(item);
auto it = fp_tree.insert(fp_tree.end(), node);
std::uint64_t node_index = std::distance(fp_tree.begin(), it);
fp_tree[parent].m_adj.insert(fp_tree[parent].m_adj.end(), node_index);
return node_index;
}
std::vector<fptree_node> fp_init(std::vector<fp_prefix>& fp_prefixes, \
const std::vector<std::vector<std::string>> T)
{
std::vector<fptree_node> tree = \
std::vector<fptree_node>(fp_init_tree(std::string("null"), 0L));
FP_PREFIX fp_prefix;
fp_prefix.m_leaf = 0;
fp_prefix.m_prefix.push_back(tree[0].m_item);
fp_prefixes.push_back(fp_prefix);
fp_prefix.m_prefix = std::vector<std::string>();
std::uint64_t curr_node = 0;
for (auto it = T[0].begin(); it != T[0].end(); it++)
{
curr_node = fp_add_node(tree, curr_node, *it, 1L);
fp_prefix.m_leaf = curr_node;
fp_prefix.m_prefix.push_back(*it);
fp_prefixes.push_back(fp_prefix);
}
return tree;
}
template<class _init="">
bool fp_is_duplicate_trans(_InIt _First, _InIt _Pos)
{
return std::find_if(pstl::execution::par_unseq, _First, _Pos - 1, \
[&](const std::vector<std::string>& trans) { \
return std::equal(pstl::execution::par_unseq, trans.begin(), trans.end(), \
_Pos->begin(), _Pos->end()); }) != _Pos - 1;
}
template<class _init="">::iterator>
_OutIt fp_find_prefix(_InIt _First, _InIt _Last, \
_PrefIt _PrefFirst, _PrefIt _PrefLast)
{
return std::find_if(pstl::execution::par_unseq,
_First, _Last, [&](FP_PREFIX fp_prefix) { \
return std::equal(pstl::execution::par_unseq,
fp_prefix.m_prefix.begin(), \
fp_prefix.m_prefix.end(), _PrefFirst, _PrefLast); });
}
template<class _init="">
bool fp_prefix_exists(_InIt _First, _InIt _Last, \
const FP_PREFIX fp_prefix)
{
return std::find_if(pstl::execution::par_unseq, _First, _Last, \
[&](FP_PREFIX fpp) { return std::equal(
pstl::execution::par_unseq, fpp.m_prefix.begin(), \
fpp.m_prefix.end(), fp_prefix.m_prefix.begin(), \
fp_prefix.m_prefix.end()); }) != _Last;
}
void fp_update_model(std::uint64_t leaf_n, \
std::vector<fptree_node>& fp_tree)
{
std::uint64_t fp_leaf = leaf_n;
while (fp_tree[fp_leaf].m_parent[0] != -1)
{
fp_tree[fp_leaf].m_count++;
fp_leaf = fp_tree[fp_leaf].m_parent[0];
}
}
void fp_build_tree(\
std::vector<fptree_node>& fp_tree, \
std::vector<std::vector<std::string>> T)
{
std::vector<fp_prefix> fp_prefixes;
fp_tree = fp_init(fp_prefixes, T);
for (auto it = T.begin() + 1; it != T.end(); it++)
{
if (fp_is_duplicate_trans(T.begin(), it))
fp_update_model(fp_find_prefix(\
fp_prefixes.begin(), fp_prefixes.end(), \
it->begin(), it->end())->m_leaf, fp_tree);
else {
std::size_t max_size = 0L;
std::uint64_t fp_leaf = 0L;
std::vector<std::string> prefix;
std::vector<std::string> ts = *it;
std::vector<std::string> curr_prefix;
std::int64_t index = it - T.begin();
while (--index >= 0)
{
curr_prefix = fp_get_prefix(*it, *(T.begin() + index));
if (curr_prefix.size() > max_size)
{
max_size = curr_prefix.size();
prefix = curr_prefix;
}
}
if (prefix.size() > 0)
fp_leaf = fp_find_prefix(fp_prefixes.begin(), \
fp_prefixes.end(), prefix.begin(), prefix.end())->m_leaf;
else fp_leaf = fp_prefixes[0].m_leaf;
FP_PREFIX fp_prefix;
for (auto ts_it = ts.begin(); ts_it != ts.end(); ts_it++)
{
if ((ts_it >= ts.begin() + prefix.size()) || (prefix.size() == 0))
fp_leaf = fp_add_node(fp_tree, fp_leaf, *ts_it, 0L);
fp_prefix.m_leaf = fp_leaf;
fp_prefix.m_prefix.push_back(*ts_it);
if (!fp_prefix_exists(fp_prefixes.begin(), \
fp_prefixes.end(), fp_prefix))
fp_prefixes.push_back(fp_prefix);
}
fp_update_model(fp_leaf, fp_tree);
}
}
for (auto t_it = fp_tree.begin(); \
t_it != fp_tree.end(); t_it++)
{
auto s_it = t_it;
bool adj_found = false;
while ((++s_it != fp_tree.end()) && (!adj_found))
if (t_it->m_item == s_it->m_item)
{
adj_found = true;
t_it->m_parent.push_back(\
std::distance(fp_tree.begin(), s_it));
}
}
}
std::vector<std::vector<std::string>> \
fp_extract_prefix_paths( \
std::vector<std::vector<std::string>> T, \
std::vector<std::string> C)
{
std::vector<arl::fptree_node> fp_tree;
std::vector<std::vector<std::string>> fp_itemsets;
std::vector<arl::fp_supp_count> fp_items_supp \
= ARL::fp_get_supp_count(ARL::get_items(T), T);
ARL::fp_convert_stream(fp_items_supp, T, C);
ARL::fp_build_tree(fp_tree, T);
#pragma omp parallel for
for (auto it = fp_items_supp.begin(); \
it != fp_items_supp.end(); it++)
{
std::uint64_t index = 0L;
auto n_it = fp_tree.begin(); std::uint64_t supp_max = 0L;
while ((n_it = std::find_if
(pstl::execution::par_unseq, n_it, fp_tree.end(),
[&](const ARL::FPTREE_NODE& node) {
return node.m_item == it->m_item; })) != fp_tree.end())
{
if (n_it->m_count > supp_max)
{
index = std::distance(fp_tree.begin(), n_it);
supp_max = n_it->m_count;
}
n_it++;
}
bool done = false;
std::uint64_t node = index;
std::vector<std::string> itemset;
while ((fp_tree[node].m_item != "null") && (done == false))
{
if (std::find(pstl::execution::par_unseq,
itemset.begin(), itemset.end(), \
fp_tree[node].m_item) == itemset.end())
itemset.push_back(fp_tree[node].m_item);
if (fp_tree[node].m_parent.size() == 1)
node = fp_tree[node].m_parent[0];
else {
std::uint64_t parent1 = fp_tree[node].m_parent[0];
std::uint64_t parent2 = fp_tree[node].m_parent[1];
node = (fp_tree[parent1].m_count >= \
fp_tree[parent2].m_count) ? parent1 : parent2;
}
}
std::vector<std::string> prefix = utils::union_vec(itemset, C);
std::vector<std::string> items = utils::intersect_vec(itemset, prefix);
#pragma omp parallel for schedule(dynamic, 4)
for (auto it2 = items.begin(); it2 != items.end(); it2++)
{
std::vector<std::string> subset = prefix;
subset.push_back(*it2);
std::uint64_t count = std::count_if(
pstl::execution::par_unseq, T.begin(), T.end(),
[&](std::vector<std::string>& trans) {
return utils::union_vec(trans, subset).size() == subset.size();
});
if (count <= ARL::min_supp * T.size())
itemset.erase(std::find(pstl::execution::par_unseq, \
itemset.begin(), itemset.end(), *it2));
}
fp_itemsets.push_back(itemset);
}
return fp_itemsets;
}
std::vector<fp_class_item> fp_growth( \
std::vector<std::vector<std::string>> T, \
std::vector<std::string> classes)
{
std::vector<arl::fp_class_item> results;
std::vector<std::vector<std::string>> rules;
if (T.size() > 1000)
{
std::uint64_t th_max = T.size() / 1000;
th_max = (th_max > omp_get_max_threads()) ? \
omp_get_max_threads() : th_max;
omp_set_num_threads(th_max);
#pragma omp parallel
{
std::uint64_t tid = omp_get_thread_num();
std::uint64_t start = tid * 1000;
std::uint64_t end = (tid + 1) * 1000;
if (end > T.size()) end = T.size();
std::vector<std::vector<std::string>> trans_chunk;
trans_chunk.insert(trans_chunk.end(), \
T.begin() + start, T.begin() + end);
std::vector<std::vector<std::string>> \
itemsets = ARL::fp_extract_prefix_paths(trans_chunk, classes);
rules.insert(rules.end(), itemsets.begin(), itemsets.end());
}
}
else {
std::vector<std::vector<std::string>> \
itemsets = ARL::fp_extract_prefix_paths(T, classes);
rules.insert(rules.end(), itemsets.begin(), itemsets.end());
}
#pragma omp parallel for
for (auto c_it = classes.begin() + 1; c_it != classes.end(); c_it++)
{
std::vector<std::vector<std::string>> itemsets;
for (auto t_it = rules.begin(); t_it != rules.end(); t_it++)
if (std::find(pstl::execution::par_unseq, \
t_it->begin(), t_it->end(), *c_it) != t_it->end())
itemsets.push_back(*t_it);
std::vector<std::string> merged = *itemsets.begin();
for (auto t_it = itemsets.begin() + 1; t_it != itemsets.end(); t_it++)
{
std::vector<std::string> isect_items = \
utils::intersect_vec(merged, *t_it);
merged = utils::append_vec(*t_it, isect_items);
}
ARL::FP_CLASS_ITEM fp_class_items;
fp_class_items.m_items = merged;
fp_class_items.m_class = std::string(*c_it);
results.push_back(fp_class_items);
}
return results;
}
}
int main()
{
std::cout << "FPGrowth Algorithm Demo v1.00a by Arthur V. Ratz\n";
std::cout << "================================================\n\n";
std::cout << "\n Enter dataset filename (*.csv): "; std::cin >> filename;
std::vector<std::string> classes = \
ARL::read_sl_csv_file(cs_filename);
std::vector<std::vector<std::string>> T = \
ARL::read_data_from_csv_file(filename);
std::cout << "\n Classes: " << classes.size() << " items" << "\n";
std::cout << " Transactions: " << T.size() << " items" << "\n\n";
std::vector<arl::fp_class_item> \
results = ARL::fp_growth(T, classes);
for (auto rl_it = results.begin(); rl_it != results.end(); rl_it++)
{
std::cout << rl_it->m_class << " => " << "[ ";
for (auto it = rl_it->m_items.begin(); \
it != rl_it->m_items.end(); it++)
std::cout << *it << " ";
std::cout << " ]\n";
}
std::cin.get();
std::cin.get();
std::cout << "*\n";
}
Conclusion
In this article, we've thoroughly discussed about the FPGrowth algorithm that serves as an efficient alternative to the famous Apriori and ECLAT algorithms. Compared to these algorithms, FPGrowth is a somewhat different algorithm, providing more algorithm-level performance optimization, making the entire process of association rules mining faster. Specifically, it allows to avoid a case in which we have a need to generate typically huge amounts of rule candidates to find the potentially interesting association rules. Instead, the association rules can be found based on the extraction of particular prefix paths directly from the tree. This drastically simplifies the process of the association rules mining, and thus, allows to sufficiently increase the performance of the following process.
During the alogorithm discussion, our goal was to demonstrate how to use the FPGrowth algorithm to perform the association rules mining in the typically huge "raw" datasets, containing over 10^6 of transactions, obtained from a real-time data streams, rather than a conditional database as it has been already discussed in the vast of documentation and guidelines. For that purpose, besides the algorithm-level optimizations, we've also used the Intel Parallel Studio XE development tools to increase the performance of the sequential legacy code written in C++11, implementing the FPGrowth algorithm.
History
- 20th July, 2019 - Initial release
