Introduction
Disclaimer: I'm going to use a lot of jargon here, and I'll do my best to explain it all, but it may not come in order so if you don't quite understand something, hold the thought and keep reading. I've done my best to avoid this but I can't anticipate every question.
So previously, I have used deterministic finite automata to implement non-backtracking regular expressions in my tokenizers. The algorithm is older, but very efficient. The only downside is the time it takes to generate the state table at least when dealing with large character ranges introduced by Unicode. This is an algorithm limitation and there's very little to be done about it, as I eventually found out.
What I needed was a way to use non-deterministic finite automata and forgo the transformation to the deterministic model altogether. That solves some of the issue, but it still doesn't allow for some of the more complicated regular expressions like word boundaries.
Then a few guys, namely, Rob Pike, Ken Thompson and Russ Cox gave me a fantastic idea that solves these problems efficiently, and in a very interesting way using a tiny virtual machine with a specialized instruction set to run a regular expression match. I've included articles on this in the further reading section. To me, this approach is fascinating, as I just love bit twiddling like this. It also potentially lends itself to compilation in the native instruction set of a "real" target machine. I haven't implemented all of that here (yet!) but this is the baseline runtime engine. I should stress that my code draws from the concepts introduced by them and I wouldn't have done it this way without exposure to that code at that link - credit where it is due.
Conceptualizing this Mess
So first, I should explain deterministic and non-deterministic finite automata.
Finite state machines are composed of graphs of states. Each state can reference another state using either an "input transition" or an "epsilon transition". An input transition consumes the specified input before moving to the destination. An epsilon transition moves to a destination state without consuming or examining any input. A machine with one or more epsilon transitions is considered "non-deterministic" (NFA) and may be in more than one state at any given time. Non-deterministic state machines are more complicated and less efficient, but there is a deterministic state machine (DFA) for any non-deterministic state machine, and an algorithm to turn an NFA into a DFA using a technique called powerset construction. I've always used this powerset construction approach to create a DFA but it just takes too long with Unicode ranges.
The closure of a state is the state itself and the unique set of all states reachable from that state, on either an epsilon or input transition. The closure represents the state machine indicated by the root state. These graphs can be recursive - meaning states can point back to themselves.
The graph for a state machine matching "foo" is just below:

But that's not very practical. For something a little closer to "real world", here's a simple DFA lexer that matches a "id", an int, or whitespace.

The nice thing about a DFA is it's only ever in one state at once, so moving between states is a simple goto like playing Chutes and Ladders. With an NFA, it can be in multiple states at once because the dashed lines below are automatically moved on once encountered, so moving between them gets much more involved. Doing so efficiently requires a certain amount of cleverness. To illustrate, here's the equivalent lexer machine as the above, represented as an NFA:

You might be wondering why anyone would construct the NFA since it's more complicated, less efficient, and there's a DFA for every NFA. Well, for several reasons. The first is, constructing an NFA programmatically from an expression is much easier to do as an NFA. To do so as a DFA would require tremendously complicated conflict resolution code, for when a state can branch to more than one state on the same character. It would have to split states and create more states to compensate. The second, is that the conversion process from NFA to DFA can be time consuming, taking much longer than a match itself, so if you're using a regular expression once and throwing it away it's impractical. This isn't really an issue with lexers, since that's never done with lexers, but with straight regex it can be a problem. It's much better in this case to run a slightly less efficient runtime algorithm than it is to optimize it beforehand, which can take longer than the less efficient match. Sometimes, such as with Unicode, even if we're pre-generating those DFAs, they can take so long to generate that even the pre-generation process has an impractical wait time.
There's another reason that's kind ancillary and that is as long as we're using an NFA, we may as well add more features since we're already spending the overhead. I'll explain:
A DFA state essentially has a single function associated with it. This function takes an input character, and returns a single destination state. We'll call it Transition() for now (not its real name.) Each time we encounter a character in the input stream, we run the Transition() function and move from our current state to its destination state, or report an error while advancing the cursor. In order to make this work for an NFA, the function would take an input character and return several destination states! This means we have to traverse multiple paths "simultaneously" in order to match. Or at least that's one way of looking at it. Another way of looking at it, is the machine has to "guess" which path to take given multiple choices, and it must always guess perfectly. The former way is actually how we do it, and it's easier than it sounds but the latter way resolves exactly the same way. There's no magic, involved I promise - it's just that it's often explained the latter way but it's the same thing in practice underneath the theory.
Anyway, we want more functions than simply transitioning on a single character. In order to enable NFA, we need a function to jump to a state unconditionally without consuming input, and a function to - get this - jump to multiple states "at the same time" without consuming input. This way, we can follow all of the dashed lines. I'm not going to get into how we jump to multiple destinations yet except to say will be using fibers, which are a little like threads, in order to accomplish it. Anyway, since we're adding these functions, we can add more complicated functions such branching on sets of ranges in order to make the matching more efficient.
We have another problem to tackle, and that is the problem of calling these functions in the first place given a regular expression. We'll be turning a regular expression into a tiny "program" using some bytecode where each function is represented by an instruction, which we then interpret in order to match. This interpreter is what runs our regular expression. Cool, right?
Converting an Expression to an Abstract-Syntax-Tree
Before we can compile our regular expression into our bytecode, we must first parse the regular expression into a sane normal form we can traverse. We represent it as a simple binary tree. That's not the most efficient structure to search, but we're not searching it. We're going to traverse all of it anyway as we emit bytecode. The class is kind of ugly, but it's never used outside the compilation process. It's not presented to any consumer other than the compiler, so it needs to be "just good enough" for the compiler to use it.
sealed class Ast
{
#region Kinds
public const int None = 0;
public const int Lit = 1;
public const int Set = 2;
public const int NSet = 3;
public const int Cls = 4;
public const int Cat = 5;
public const int Opt = 6;
public const int Alt = 7;
public const int Star = 8;
public const int Plus = 9;
public const int Rep = 10;
public const int UCode = 11;
public const int NUCode = 12;
#endregion Kinds
public int Kind = None;
public bool IsLazy = false;
public Ast Left = null;
public Ast Right = null;
public int Value = '\0';
public int[] Ranges;
public int Min = 0;
public int Max = 0;
...
This is such a throwaway class I don't even create an enum for the different kinds of node it can be. This is okay, as we'll see. The Kind represents the sorts of operations we can do with a regular expression, including alternation, concatenation, sets, "not" sets, optional, star, plus, and others. Since this is primarily intended for lexing, we don't do capture groups or anchors but if we did, we'd add a kind for them here. For unary expressions, only Left is used. Otherwise, for binary expressions, Left and Right are both used. For literals and Unicode categories, Value is used, and for sets and not sets, Ranges is used. IsLazy is for quantified matches and indicate whether the match is non-greedy or not. This is just enough information to take our regex and compile it. We generate these structures through the static Parse() routine which is recursive descent, and kind of involved. Characters are stored as ints for future extensibility. I hope to eventually support 32-bit Unicode values here.
Note the CharCls.cs file in the code. This is a generated file, which I created the LexTableGen tool specifically to generate. What the tool does is create a bunch of packed ranges for various named character classes as well as Unicode categories. This is so we can save a little bit of startup time by avoiding generating these on assembly load. These ranges are used by the parser to fill in the AST with the appropriate data when named character sets are used. I have not filled in all the character classes yet as this build is preliminary so things like \d or [[:digit:]] don't work properly as of now. I'll be adding that support soon, but it didn't matter for the demo. [[:IsDigit:]] is the Unicode equivalent and that works.
Defining the Machine Instruction Set
Now on to the fun stuff. This is covered in Russ Cox's article wherein he covers Rob Pike's theoretical virtual machine but I've augmented the theoretical machine quite a bit, and included much more complex instructions that can take arrays of operands. This is one of the nice side effects of using a garbage collected system like .NET - the nested arrays that facilitate this are easy, unlike in C.
When we generate lexer code, we don't want that code to have any dependencies on a library. For this reason, we do not create classes for our instructions. Instead, each instruction is encoded as an array of type int[] where index 0 is the opcode and the remaining indices contain the operands. These arrays themselves are stored in a program array of type int[][]. This program array represents the program for the regular expression. You can run this program to match text, or you can dump it to a string if you want to see the code it generated.
Let's look at some code. Here's the code for part of that lexer above. An "id" of the form [A-Z_a-z][0-9A-Z_a-z]*:
L0000: set "A".."Z", "_", "a".."z"
L0001: split L0002, L0004
L0002: set "0".."9", "A".."Z", "_", "a".."z"
L0003: jmp L0001
L0004: match 0
Can you see the loop? Notice how at L0003, we jmp back to L0001. That's part of the * we stuck at the end of the regular expression.
The other part of the loop is the enter condition, designated by the split instruction. Here, we're telling the machine to follow two paths - both L0002 and L0004. Since L0002 is listed first in the split instruction, it takes priority. This indicates a greedy match the way it's configured. If we wanted to make it a lazy match, we'd simply swap out the two operands in split.
Here's a list of the instructions the machine currently supports:
match <symbol> - Indicates the machine should match and report the specified symboljmp <addr> - Indicates that the machine should jump to the specified addresssplit <addr1>, <addr2>, ... <addrN> - Indicates that the machine should jump to each of the specified addresses and execute them concurrently.char <ch> - Indicates that the machine should match a single character and advance or failany - Matches any character and advances. Fails on end of input.set <packedRange1>, <packedRange2>, ... <packedRangeN> - Indicates that the machine should match one of the ranges and advance or failnset <packedRange1>, <packedRange2>, ... <packedRangeN> - Indicates that the machine should fail if it matches one of the ranges, or otherwise advanceucode <cat> - Indicates that the machine should match a particular Unicode category and advance or failnucode <cat> - Indicates that the machine should fail if it matches a particular Unicode category, otherwise advancesave <slot> - Saves the character location in the given slot. Slot is any integer value, and indicates the register # to store the position in.
Note that there are other opcodes that currently are not being used. These will be implemented in a future revision.
Emitting the Instruction Set
Compiling involves traversing the AST and emitting instructions depending on the kind of node it is. In Compiler, we have the inner emit routine for emitting the core instructions to "run" an AST node, and then an outer routine to emit the surrounding code that makes the lexer work.
Here's the inner routine:
internal static void EmitPart(Ast ast, IList<int[]> prog)
{
int[] inst,jmp;
switch(ast.Kind)
{
case Ast.Lit:
inst = new int[2];
inst[0] = Char;
inst[1] = ast.Value;
prog.Add(inst);
break;
case Ast.Cat:
if(null!=ast.Left)
EmitPart(ast.Left,prog);
if(null!=ast.Right)
EmitPart(ast.Right,prog);
break;
case Ast.Alt:
if (null == ast.Right)
{
if (null == ast.Left)
{
return;
}
inst = new int[3];
inst[0] = Split;
prog.Add(inst);
var i = prog.Count;
EmitPart(ast.Left, prog);
inst[1] = i;
inst[2] = prog.Count;
return;
}
if (null == ast.Left)
{
inst = new int[3];
inst[0] = Split;
prog.Add(inst);
var i = prog.Count;
EmitPart(ast.Right, prog);
inst[1] = i;
inst[2] = prog.Count;
return;
}
else
{
inst = new int[3];
inst[0] = Split;
prog.Add(inst);
inst[1] = prog.Count;
EmitPart(ast.Left, prog);
jmp = new int[2];
jmp[0] = Jmp;
prog.Add(jmp);
inst[2]= prog.Count;
EmitPart(ast.Right,prog);
jmp[1] = prog.Count;
}
break;
case Ast.NSet:
case Ast.Set:
inst = new int[ast.Ranges.Length + 1];
inst[0] = (ast.Kind==Ast.Set)?Set:NSet;
Array.Sort(ast.Ranges);
Array.Copy(ast.Ranges, 0, inst, 1, ast.Ranges.Length);
prog.Add(inst);
break;
case Ast.NUCode:
case Ast.UCode:
inst = new int[2];
inst[0] = (ast.Kind == Ast.UCode) ? UCode : NUCode;
inst[1] = ast.Value;
prog.Add(inst);
break;
case Ast.Opt:
if (null == ast.Left)
return;
inst = new int[3];
inst[0] = Split;
prog.Add(inst);
inst[1] = prog.Count;
EmitPart(ast.Left, prog);
inst[2] = prog.Count;
if (ast.IsLazy)
{
var t = inst[1];
inst[1] = inst[2];
inst[2] = t;
}
break;
case Ast.Star:
ast.Min = 0;
ast.Max = 0;
goto case Ast.Rep;
case Ast.Plus:
ast.Min = 1;
ast.Max = 0;
goto case Ast.Rep;
case Ast.Rep:
if (ast.Min > 0 && ast.Max > 0 && ast.Min > ast.Max)
throw new ArgumentOutOfRangeException("Max");
if (null == ast.Left)
return;
int idx;
Ast opt;
Ast rep;
switch (ast.Min)
{
case -1:
case 0:
switch (ast.Max)
{
case -1:
case 0:
idx = prog.Count;
inst = new int[3];
inst[0] = Split;
prog.Add(inst);
inst[1] = prog.Count;
EmitPart(ast.Left, prog);
jmp = new int[2];
jmp[0] = Jmp;
jmp[1] = idx;
prog.Add(jmp);
inst[2] = prog.Count;
if (ast.IsLazy)
{
var t = inst[1];
inst[1] = inst[2];
inst[2] = t;
}
return;
case 1:
opt = new Ast();
opt.Kind = Ast.Opt;
opt.Left = ast.Left;
opt.IsLazy = ast.IsLazy;
EmitPart(opt,prog);
return;
default:
opt = new Ast();
opt.Kind = Ast.Opt;
opt.Left = ast.Left;
opt.IsLazy = ast.IsLazy;
EmitPart(opt, prog);
for (var i = 1; i < ast.Max; ++i)
{
EmitPart(opt,prog);
}
return;
}
case 1:
switch (ast.Max)
{
case -1:
case 0:
idx = prog.Count;
EmitPart(ast.Left, prog);
inst = new int[3];
inst[0] = Split;
prog.Add(inst);
inst[1] = idx;
inst[2] = prog.Count;
if (ast.IsLazy)
{
var t = inst[1];
inst[1] = inst[2];
inst[2] = t;
}
return;
case 1:
EmitPart(ast.Left, prog);
return;
default:
rep = new Ast();
rep.Min = 0;
rep.Max = ast.Max -1;
rep.IsLazy = ast.IsLazy;
rep.Left = ast.Left;
EmitPart(ast.Left, prog);
EmitPart(rep, prog);
return;
}
default:
switch (ast.Max)
{
case -1:
case 0:
for (var i = 0; i < ast.Min; ++i)
EmitPart(ast.Left,prog);
rep = new Ast();
rep.Kind = Ast.Star;
rep.Left = ast.Left;
rep.IsLazy = ast.IsLazy;
EmitPart(rep,prog);
return;
case 1:
throw new NotImplementedException();
default:
for (var i = 0; i < ast.Min; ++i)
EmitPart(ast.Left, prog);
if (ast.Min== ast.Max)
return;
opt = new Ast();
opt.Kind = Ast.Opt;
opt.Left = ast.Left;
opt.IsLazy = ast.IsLazy;
rep = new Ast();
rep.Kind = Ast.Rep;
rep.Min = rep.Max = ast.Max - ast.Min;
EmitPart(rep, prog);
return;
}
}
throw new NotImplementedException();
}
}
You can see most of the complication of this routine is rendering repetition, such as (foo){10,} simply since there are so many combinations of Min and Max to account for. The rest is relatively straightforward considering; The function calls itself to render child expressions, it renders a split whenever it has to make a choice between two expressions, it renders a jmp instruction when it needs to loop or skip a branch, and it often creates split and jmp instructions where the destination address refers just past the final instruction. This is so we can chain expressions together. The final location in the branch actually refers to the first location of the next instruction which isn't present yet. This is okay. It will never be invalid since the outer emit routines always add at least one instruction to the end.
To emit a lexer, we have to start with a primary split between all of the different symbols. We also have to emit match instructions that report the symbol matched. Furthermore, we have to save the start and end positions of each match. The code for doing that is still much simpler than the above:
internal static int[][] EmitLexer(params Ast[] expressions)
{
var prog = new List<int[]>();
int[] match, save;
var split = new int[expressions.Length + 2];
split[0] = Compiler.Split;
prog.Add(split);
for (var i = 0; i < expressions.Length; i++)
{
split[i + 1] = prog.Count;
save = new int[2];
save[0] = Save;
save[1] = 0;
prog.Add(save);
EmitPart(expressions[i], prog);
save = new int[2];
save[0] = Save;
save[1] = 1;
prog.Add(save);
match = new int[2];
match[0] = Match;
match[1] = i;
prog.Add(match);
}
split[split.Length - 1] = prog.Count;
save = new int[2];
save[0] = Save;
save[1] = 0;
prog.Add(save);
var any = new int[1];
any[0] = Any;
prog.Add(any);
save = new int[2];
save[0] =Save;
save[1] = 1;
prog.Add(save);
match = new int[2];
match[0] = Match;
match[1] = -1;
prog.Add(match);
return prog.ToArray();
}
That's not that bad once you get the hang of it.
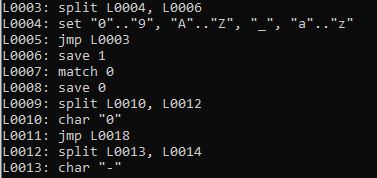
Here's the entire dump of the machine code for the lexer indicated by the NFA lexer graph I presented earlier:
L0000: split L0001, L0008, L0020, L0024
L0001: save 0
L0002: set "A".."Z", "_", "a".."z"
L0003: split L0004, L0006
L0004: set "0".."9", "A".."Z", "_", "a".."z"
L0005: jmp L0003
L0006: save 1
L0007: match 0
L0008: save 0
L0009: split L0010, L0012
L0010: char "0"
L0011: jmp L0018
L0012: split L0013, L0014
L0013: char "-"
L0014: set "1".."9"
L0015: split L0016, L0018
L0016: set "0".."9"
L0017: jmp L0015
L0018: save 1
L0019: match 1
L0020: save 0
L0021: set "\t", "\n", "\v", "\f", "\r", " "
L0022: save 1
L0023: match 2
L0024: save 0
L0025: any
L0026: save 1
L0027: match -1
Note how we've saved the character positions at the beginning and end of each lexer symbol segment. This is so we can get the capture back, given these start and end positions. The Regex.CompileLexer() inserts these into the instruction stream automatically. We also have a final match starting at L0024 which handles our error condition, also inserted by the above function. It simply matches any character and returns -1 as the symbol. It is the lowest priority so it only matches if nothing else has.
Executing the Machine Code
In order to support multiple paths (entered via split) our machine virtualizes several fibers, which are similar to threads except cooperatively scheduled. Each fiber is responsible for running one of the paths. Above, we'd have the main fiber running the path starting at L0001 and additional ones starting at L0008, L0020 and L0024 due to the split.
Virtually, each thread of execution, represented by a fiber, tries to run a match against the current input, following the instructions laid out before it. You can visualize them running concurrently, but under the covers, they all run in lockstep so that we don't have to backtrack over the input stream. If this were truly concurrent, it would require backtracking. This is more efficient and yields the same result. Since creating a fiber doesn't really cost anything, we don't have to worry about creating and destroying them frequently, which we'll do. A fiber typically runs one instruction and then spawns another fiber to run the next instruction. This may seem inefficient, but it's more efficient than the alternative which would involve removing fibers from an array backed list. These are structs anyway so we aren't hammering the heap with object creations.
We prioritize the fibers in order to make sure our matches stay lazy or greedy as required. If we didn't do this, we'd run into trouble in terms of that because our jumps would essentially get reordered and we can't have that.
In order to make sure we've got the longest match we asked for, we just keep running until all the fibers have exited.
Our instruction stream is represented by an array of nested int[] arrays, and the current instruction pointer is simply an integer index into that array. Remember each nested int[] represents one instruction. Each fiber has a pointer to the main instruction array and its own instruction pointer into that array. It also has a Saved list which holds all the saved positions that were stored by the save instruction. We store these by fiber so that we can visit multiple paths concurrently without messing up the save positions.
We hold the current fibers in an alternating pair of lists in order to both maintain priority and to keep things efficient. Using a single list would require copies due to inserts and we don't want that. Instead, we just create two lists, and swap references to them on every cycle, clearing one of them. This idea I got from Russ Cox's C code, and I used it, because it's a good one.
Basically, we build up a queue of fibers to be executed, and then we let each one pass over the current input character, filtering for matches (both single character matches, like char or set and entire matches indicated by match) - here's the entire Lex() routine that runs the VM:
public static int Lex(int[][] prog,LexContext input)
{
input.EnsureStarted();
int i,match=-2;
List<_Fiber> clist, nlist, tmp;
int[] pc;
int sp=0;
var sb = new StringBuilder();
IList<int> saved, matched;
matched = null;
saved = new List<int>();
clist = new List<_Fiber>(prog.Length);
nlist = new List<_Fiber>(prog.Length);
_EnqueueFiber(clist, new _Fiber(prog,0, saved), 0);
matched = null;
var cur = -1;
if(LexContext.EndOfInput!=input.Current)
{
var ch1 = unchecked((char)input.Current);
var ch2 = '\0';
if (char.IsHighSurrogate(ch1))
{
input.Advance();
ch2 = unchecked((char)input.Current);
cur = char.ConvertToUtf32(ch1, ch2);
}
else
cur = (int)ch1;
}
while(0<clist.Count)
{
bool passed = false;
for (i = 0; i < clist.Count; ++i)
{
var t = clist[i];
pc = t.Instruction;
saved = t.Saved;
switch (pc[0])
{
case Compiler.Char:
if (pc.Length!=0 && cur!= pc[1])
{
break;
}
goto case Compiler.Any;
case Compiler.Set:
if (!_InRanges(pc, cur))
{
break;
}
goto case Compiler.Any;
case Compiler.NSet:
if (_InRanges(pc, cur))
{
break;
}
goto case Compiler.Any;
case Compiler.UCode:
var str = char.ConvertFromUtf32(cur);
if (unchecked((int)char.GetUnicodeCategory(str,0) != pc[1]))
{
break;
}
goto case Compiler.Any;
case Compiler.NUCode:
str = char.ConvertFromUtf32(cur);
if (unchecked((int)char.GetUnicodeCategory(str,0)) == pc[1])
{
break;
}
goto case Compiler.Any;
case Compiler.Any:
if (LexContext.EndOfInput==input.Current)
{
break;
}
passed = true;
_EnqueueFiber(nlist, new _Fiber(t, t.Index+1, saved), sp+1);
break;
case Compiler.Match:
matched = saved;
match = pc[1];
i = clist.Count;
break;
}
}
if (passed)
{
var s = char.ConvertFromUtf32(cur);
sb.Append(s);
input.Advance();
if (LexContext.EndOfInput != input.Current)
{
var ch1 = unchecked((char)input.Current);
var ch2 = '\0';
if (char.IsHighSurrogate(ch1))
{
input.Advance();
++sp;
ch2 = unchecked((char)input.Current);
cur = char.ConvertToUtf32(ch1, ch2);
}
else
cur = (int)ch1;
}
++sp;
}
tmp = clist;
clist = nlist;
nlist = tmp;
nlist.Clear();
}
if (null!=matched)
{
var start = matched[0];
var end = matched[1];
input.CaptureBuffer.Append(sb.ToString(start, end - start));
return match;
};
return -1;
}
And here's the _EnqueueFiber() routine it calls:
static void _EnqueueFiber(IList<_Fiber> l, _Fiber t, int sp)
{
l.Add(t);
switch (t.Instruction[0])
{
case Compiler.Jmp:
_EnqueueFiber(l, new _Fiber(t, t.Instruction[1],t.Saved),sp);
break;
case Compiler.Split:
for (var j = 1; j < t.Instruction.Length; j++)
_EnqueueFiber(l, new _Fiber(t.Program, t.Instruction[j],t.Saved),sp);
break;
case Compiler.Save:
var saved = new List<int>(t.Saved.Count);
for (int ic = t.Saved.Count, i = 0; i < ic; ++i)
saved.Add(t.Saved[i]);
var slot = t.Instruction[1];
while (saved.Count < (slot + 1))
saved.Add(0);
saved[slot] = sp;
_EnqueueFiber(l, new _Fiber(t,t.Index+1, saved), sp);
break;
}
}
One weird bit here, other than the overarching weirdness of this project, is the Save implementation, which has to store the current string position represented by sp. It copies any existing saved positions, ensures that there are enough slots in the list, and then sets the specified slot to sp. I do it this way to allow for an arbitrary number of slots for future proofing this code. When we do full regex matching down the road, we'll want at least 10 or so backreferences and that means storing 20 positions - the start and end for each. In addition, we may implement named capture groups which will also require more storage. Another weird bit is handling Unicode surrogates, which we do whenever we advance. cur holds the current integer UTF-32 value.
Coding this Mess
This is part of my larger LexContext package, which is primarily meant for implementing your own lexers and parsers.
The LexDemo.csproj code demonstrates using this code. It's pretty easy:
static void Main(string[] args)
{
var prog = Regex.CompileLexer(
@"[A-Z_a-z][A-Z_a-z0-9]*",
@"0|(\-?[1-9][0-9]*)",
@"[ \t\r\n\v\f]"
);
Console.WriteLine(Regex.ProgramToString(prog));
var text = "fubar bar 123 1foo bar -243 @ 0";
Console.WriteLine("Lex: " + text);
var lc = LexContext.Create(text);
while(LexContext.EndOfInput!=lc.Current)
{
lc.ClearCapture();
Console.WriteLine("{0}: \"{1}\"", Regex.Lex(prog, lc), lc.GetCapture());
}
}
This will lex as follows:
Lex: fubar bar 123 1foo bar -243 @ 0
0: "fubar"
3: " "
0: "bar"
3: " "
1: "123"
3: " "
1: "1"
0: "foo"
3: " "
0: "bar"
3: " "
1: "-243"
3: " "
-1: "@"
3: " "
1: "0"
Room for Improvement
This code could stand some further development. For starters, there are certain instructions like dot which can be easily used by the AST but aren't. There also needs to be more character classes added. Eventually, it would be nice to include some shortest string algorithms for optimization, a compilation option that will compile to IL or .NET source code, and some more matching as opposed to simply tokenizing features.
Performance
I've compared the relative performance of both a DFA engine based on my previous Regex engine.
Lex: fubar bar 123 1foo bar -243 @#*! 0
DFA Lexed in 0.004 msec
Lex: fubar bar 123 1foo bar -243 @#*! 0
NFA Lexed in 0.049 msec
As you can see, the DFA is more than 10 times faster, and while there's room for improvement in our little machine, it can never be as fast as a DFA.
Points of Interest
Regular expressions have a lot of history associated with them and their evolution. It's rich enough that I found Russ's articles on them interesting from a historical perspective. The code reaches back into the 1970s, '80s and '90s as regular expressions evolved, most deriving from a few (in)famous implementations like awk.
Further Reading
History
- 18th January, 2019 - Initial submission
