There are many ways to traverse through a binary tree. In this post, we focus on learning how to do a postorder traversal of a binary tree.
Binary Trees are one of the common categories of datastructures to know for that comes up in coding interviews. No matter what type of questions get asked, to solve them, we usually have to traverse through everything in our given tree.
There are many ways to traverse through a tree but in this article, we will focus on learning how to do a postorder traversal of a binary tree by answering the LeetCode question, Maximum Depth of a Binary Tree.
Problem Statement
In the problem, we are given a binary tree and we want to find its maximum depth.
The tree is represented by multiple TreeNodes connected to each other.
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
}
The maximum depth of a tree is the number of nodes is longest path from the root node down to the leaf node.
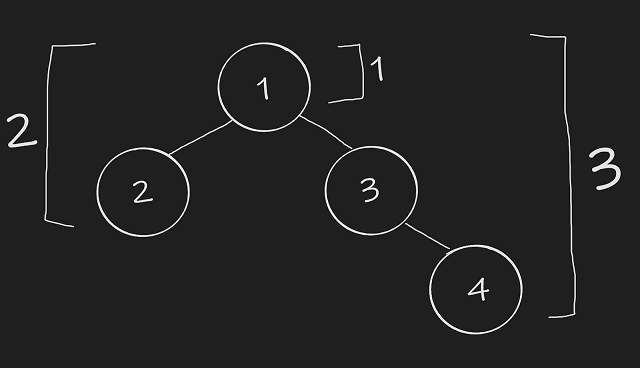
Heights of a Binary Tree
High Level Algorithm
Every TreeNode has two children, each of which has varying heights. We won’t be able to know the height of each node until we travel to the leaf node of a tree.
Once we reach the leaf node, we know that our height is 1. From there, we can start counting the heights of each of our TreeNodes as we go back up the tree.

Calculating the height of a tree
Tree problems usually require usage of recursion. To write a recursive program, we always need to think about the base case (when we can stop traversing the tree) and the recursive case (where we process data and continue traversing the tree).
Base Case
The base case in this situation is when we reach the smallest height we can encounter. A tree with a height of 0 (a null Tree Node).
Recursive Case
The recursive case here is where we calculate the height of the left and right child node. This will continue until we hit our base case (null tree node) which will return us a height of 0.

The goal of the problem is to find the maximum height of the tree. Once we have the height of both the left and right child, we find the largest of the two and add 1 to include the current Tree Node itself.
What was described here is a Post Order traversal of a tree.
- Get the height of the left child.
- Get the height of the right child.
- Processing the height and return the maximum height back.
Implementation
class Solution {
public int maxDepth(TreeNode root) {
return helper(root);
}
private int helper(TreeNode root) {
if (root == null) {
return 0;
} else {
int left = helper(root.left);
int right = helper(root.right);
return Math.max(left, right) + 1;
}
}
}
Runtime and Space Complexity
Runtime
The runtime of this algorithm is O(N), because we have to explore every single Tree Node of this tree.
Space Complexity
The worst case space complexity of this algorithm is O(N). In the worst case, we will have a line of trees that only have one child and we would have to explore all of the Tree Nodes.

Conclusion
There are a couple of key lesson to be taken away from solving the Maximum Depth of a binary Tree:
- How to do a DFS postorder traversal of a binary tree
- How to bubble back up variable back up from a leaf node
- How to define and create base and recursive case to handle recursion
While tree problems don’t get asked too often in coding interviews, trees are a subset of graph problems, which ARE common. Being able to handle recursion and bubbling up results will help you crack your next coding interview!
