Call Distribution Parameters using Combined Data Points Splicing

• Download source code - 159.3 KB

Introduction

Imagine we have a set of physical values distributed according to a lognormal. Or maybe normal, or gamma.
We need to determine the type of distribution and call (find out) its parameters.

Background

First, we build the frequency distribution of values. Second, by the graphical view of distribution, we determine its parameters. Finally, we compare the original distribution with each of the calculated ones and choose the best match.

On a closer look at the points:

1. The frequency distribution (probability distribution) is constructed in a typical way using a sorted associative container (e.g., std::map in C++).

2. Perhaps there is more than one method for determining the distribution parameters by their appearance. I have come up with only one – by the coordinates of the characteristic points.

   All distributions belong to two-parameter family. For all of them, in addition to the main probability density function, both parameters are also related by the Mode (most frequency value) equation. So, two points are sufficient to solve a system of two equations. One of them is obvious – this is a summit (the curve’s vertex) corresponding to the Mode. The second one should belong to the ascending (left) or descending (right) branch of the curve, in the location with the highest sensitivity to the distribution parameters. There are half-height locations. Of these, it is better to choose the right one, since for lognormal and gamma distributions, the descending branch is typically flatter, which provides a lower measurement inaccuracy along the abscissa.

   Let us denote by M the x-coordinate of the Mode, X – the x-coordinate of the right half-height point.
   Thus, for normal distribution, we have:

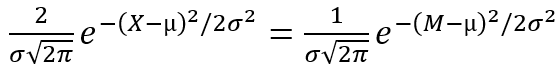     and  µ = M,

   whence the σ equation is derived:

   

   For lognormal distribution, we have:

     and   

   which finally implies:

   

   For gamma distribution, we have:

     and  

   which finally implies:

   

3. Comparison of two curves is an issue generally accepted by Pearson's method.

Conceptually looks pretty simple.

Unfortunately, the world is a dirty messy complicated place. Due to some physical and technical reasons, actual distributions are often far from ideal. Besides, they are often noisy, sometimes modulated. Moreover, they may be cropped or distorted to the left (see DNA fragment distribution and DNA fragment’s read distribution; all data presented is real). Well, distortion and clipping on the left are eliminated by selecting the second point on the descending branch. But for all other cases, finding the "true" coordinates of the characteristic points is a nontrivial task.

The issue is to build a “smoothness” virtual curve that most closely fits the data according to a specific criterion, namely the equidistance of virtual points from their real prototypes (“smoothness” means the minimum possible total distance between virtual points along the entire curve). In general, there are three methods for solving this issue: nonlinear regression, Bézier curve, and moving averaging. Now let us take into account the peculiar task simplification: (a) each real point has a unique abscissa, (b) in the crucial area including characteristic points the real points are located evenly along the x-axis, (c) each virtual point corresponds to one real (with the same abscissa, but with a corrected ordinate). For such conditions, both regression and Bezier analyzes look overly complex, and therefore, resource-intensive. Besides, Bezier curves are powerless in the case of a modulated distribution. The best solution seems to be the use of splining methods based on rolling averaging.

Simple moving average copes with the task perfectly while the total deviations of the real ordinates from the virtual ones within the moving window do not exceed the difference between the ordinates of the adjacent virtual points. In the presence of strong local deviations ("peaks"), however, the method becomes powerless. What eliminates peaks well is the moving median, although it does not actually average the data.

The solution is to consistently combine both methods. The pre-calculated median is fed to the input of the averager at every window shift. The figure shows the results of each splicing, as well as combined one, for very noisy data (a) and for smooth, but deeply modulated (b).
Interestingly, the variant with calculating the median in the "look-ahead" window (starting at the point where the averaging window ends) leads to the same results as swarming in the same window. But it requires additional control over the end of the sequence (assuming an iterator instead of a value as a Push() method input). So, it was discarded.

It remains to solve the problem with the length of the moving (sliding) window. The smaller it is, the less is the deviation of the average peak ordinate from the "real" one, which entails a more accurate determination of the half-height (the ordinate of the second characteristic point). On the other hand, on non-smooth or modulated data, a small window length can lead to "fake" local extrema. Which implies an inaccurate determination of the mode location, and then an inaccurate distribution approximation (see Figure). The problem is solved in two stages: first, the maximum reliable window length is determined based on the nature of the data, then it decreases cyclically with the calculation of the Pearson's correlation coefficient (PCC) at each step. The cycle ends either when the minimum window length is reached, or when three steps in a row are reached, at which the PCC is less than the maximum one. Experiments have shown that this is enough – after three consecutive drops in the PCC, while reducing window length, it never rises. The maximum PCC gives us the parameters of the best approximation of the applied distribution to the real one. By applying all three laws, we can ultimately answer the question of what is the most possibly “true” nature of a given real distribution – normal, lognormal, or gamma.

Splicers Implementation

Moving Average and Moving Median splicers are implemented as simple classes inherited from Moving Window and having a single Push() method. The window length is always odd. The constructor takes half the length, so for the minimum half-length of 1, the minimum window length is 3.

// Method declarations and definitions are merged
// solely for the purpose of shortening the presented code

// Moving window (sliding subset)
class MW : protected vector<ULONG>
{
protected:
    // Constructor by moving window half-length ("base")
    MW(size_t base) { insert(begin(), Size(base), 0); }

    // Adds last value and pops the first one (QUEUE functionality)
    void PushVal(ULONG x) {
        move(begin() + 1, end(), begin());
        *--end() = x;
    }

public:
    // Returns length of moving window
    //   @base: moving window half-length
    static size_t Size(size_t base) { return 2 * base + 1; }
};

// Simple Moving Average splicer
class MA : public MW
{
    ULONG _sum = 0;                    // sum of adding values
public:
    // Constructor by moving window half-length ("base")
    inline MA(size_t base) : MW(base) {}

    // Adds value and returns average
    float Push(ULONG x) {
        _sum += x - *begin();
        PushVal(x);
        return float(_sum) / size();
    }
};

// Simple Moving Median splicer
class MM : public MW
{
    vector<ULONG> _ss;                 // sorted sliding subset
public:
    // Constructor by moving window half-length
    MM(size_t base) : MW(base) { _ss.insert(_ss.begin(), size(), 0); }

    // Adds value and returns median
    ULONG Push(ULONG x) {
        PushVal(x);
        copy(begin(), end(), _ss.begin());
        sort(_ss.begin(), _ss.end());
        return _ss[size() >> 1];        // mid-size
    }
};

The coordinates of the averaged (virtual) point are mined in two operators within a traversing real points:

// Defines key points
//   @base: moving window half-length
//   @summit: returned X,Y coordinates of spliced (smoothed) summit
//   return: key points: X-coord of highest point, X-coord of right middle hight point
fpair LenFreq::GetKeyPoints(size_t base, point& summit) const
{
    point p0(*begin()), p(0, 0);         // previous, current spliced point
    MA ma(base);
    MM mm(base);

    summit.second = 0;
    for (const value_type& f : *this) {  // loop on real points
        p.first = f.first – 2 * base;               // X: minus MA & MM base back shift
        p.second = ma.Push( mm.Push(f.second) );    // Y: spliced
        if (p.second >= summit.second)    summit = p;
    }

    return fpair(
        float(summit.first),             // summit X
        // final point with half height; proportional X
        p0.first + p0.second / (p.second + p0.second)    
    );
}

A slightly simplified test version is applied. The full implementation of the callDist utility can be found on GitHub.

Efficiency

The run-time for calling the lognormal parameters was measured on a 2.5 GHz laptop.
The best and worst running times of the entire algorithm, averaged over 1000 repetitions, are shown in the table:

* “noisy” data used in the illustration of this article

Acknowledgments

I am grateful to Oleg Tolmachev (University of Greenwich, UK) for his kind assistance in refining the language of this paper.

History

• 29^th March, 2021: Initial version