Introduction
In this article, I will explore how to do integration test of systems with state using model-based techniques. We will take the outset in a simple state machine model and move on to a place-transition model, reap the benefits of working in an integration scenario add the combinatorial test design from the first article in the series and finally sprinkle with a dependency analysis and add support for asynchronous environments. What you get from this is an approach to integration test where you can leave the tedious work of setting up preconditions to the computer. On top of that you get a framework that is easily leveraged into a load simulation and where iterating the test improves test coverage.
Background
In my previous article about combinatorial test, I explored how to abstract data using categorization with BVA and ECP and discussed how the concept of covering arrays reduces the amount of necessary tests and provides an empirically based estimate of coverage. This works fine for stateless functions, but as you have probably realized the real world is very often stateful.
State Machines
As the working example throughout this article I will use a bug report in a bug tracking system. What characterizes a bug report? It’s got some details like the affected system, component, version, platform, and so on, and then it has a status field. Usually something like New, Verified, Fixed, Confirmed, Rejected and Closed depending on how you set it up. The status (or the state which I will call it from now on) determines what you can and must do to the bug report: There are limitations on how you can change between states and there may be requirements on what you must do in other states (like add a comment). The natural model for this is a state machine like this:
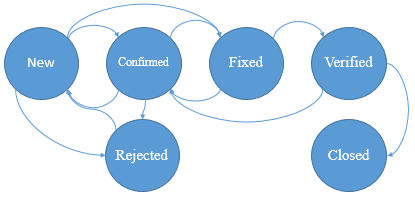
It is clear that we must at least add one test for each arch above. With one test per arc, we achieve 0-switch coverage, which is only sufficient if you are sure that history has no impact: Consider the arc from Confirmed to Rejected. If there is only one test of this transition there is no telling how the bug report got to the “Confirmed” state, it can get there from either New, Fixed or Verified. If history is a concern, more tests are required to achieve a higher switch coverage. With 1-switch coverage the test takes one historic state-change into account, 2-switch considers two changes etc.
Assume for a moment that we implement a simple state-machine and hook up all the arcs to a method that would change the state and validate, then we would have achieved a simple model-based test. Whenever the machine reaches a state with more than one outgoing arc the machine has to choose what arc to follow. If it uses a deterministic approach like graph colouring we can be sure it terminates, but it can then only guarantee 0-switch coverage. On the other hand, if it simply takes a random path we cannot be sure that it terminates, but the longer it runs the more paths are tested and the switch coverage will increase. This is known as a Markov Chain Statistical Test or MCST.
The downside is that state machines respond poorly to complexity (i.e. number of factors or different state variables to represent). The number of states grows exponentially with the number of factors while the number of arcs grow with the square of the number of states, so state machines get bad fast.
P/T Nets
Something better is needed if we want to handle real scenarios, so let‘s modify the figure:
<o:p>

What we have here is a Place/Transition net also known as a Petri net. I looks like a state machine with labels but is very different. Where a state machine is concerned with the state of a single object and how it can transition between states, the nodes in the P/T net are placeholders for multiple objects. The labels (called transitions) are actions that can fire whenever the input node contains an object. Transitions can consume any number of objects from any number of places and can similarly output any number of objects to other places.
In the figure, I added a “Create” transition that does not require any input and initially this is the only transition that can fire. Once fired there will be an object in the place “New” that can be consumed by either the “Reject”, “Confirm” or “Fix” transitions, and once any of these have fired, other transitions are enabled etc.
P/T nets like this are great for simulation: In each iteration determine the enabled transitions, pick one at random and fire it, then repeat. It will also work concurrently so if you implement such a simulator and pay a bit of attention to performance and threading you have yourself a load simulator.
P/T nets easily cope with transitions that require multiple objects like associating bug reports with each other:

Whenever there is an object in the “Confirmed” place and another object in the “Fixed” place, the “Associate” transition becomes enabled and ready to fire.
Cool right? You can do powerful testing with such a simulator and the stochastic element has the nice property that the longer you let the simulation run, the more different sequences it covers.
P/T Nets with Dependency Resolution
As long as the simulation is entirely stochastic, you cannot be sure that all transitions (i.e. all tests) will fire, but that is not too hard to fix. Assume you need to ensure that “Fix” against a “Confirmed” bug is fired. To do that we need a “Confirmed” bug that we can get either by confirming a “New” bug, or reopening a “Fixed” or “Verified” bug. Which should we choose? A rank based dependency analysis will do the trick: Apply ranks to all transitions and let rank 0 be those actions that do not consume any tokens such as the “Create” transition. Rank 1 is all transitions that are enabled by the output of the actions in rank 0 and so on.

If you need to execute a rank 3 transition that is not enabled then you need to find a rank 2 or lower transition that produces an enabling object and so on. It is easy to do recursively and if the transition requires multiple objects simply repeat the procedure one object at a time. Further, if you cannot rank a transition this way, it means that there is no way of producing the required input for it and it is dead. With this in place, it is straightforward to ensure that all live transitions fire at least once.
Adding dependency resolution to the P/T net provides some cool opportunities: You can select a transition (i.e. a test) and have the simulator set up all the prerequisites automatically – no more tedious arrange code! With a bit of bookkeeping you can also extend the simulator to do a frequency based load simulation where you just state the percentages of a few select transitions (like 50% Confirm, 20% Fix, 30% reject) and let the simulator figure out the in-betweens to achieve the specified load scenario. This is a lot easier and far more realistic than the usual approach of setting up detailed flows. Like for the state machine variant, this is also an instance of a Markov Chain Statistical Test (MCST).
Using the Code
Up until now, everything is straightforward and building a simple stochastic P/T net simulator is not much work. I have added the code for a P/T net simulator with the article that you can use as basis for your own work. It loads a network specified in XML and contains the rank analysis, dependency resolution and support MCST / frequency-based scenarios I discussed above. The code works by building a “Fixture” containing all acquired arguments for the method call so far. When all arguments are bound, the fixture is ready to execute. You will need to add error handling in case your (test) methods throw exceptions, and for heavy load you will need to make it multi-threaded. That should be straight-forward.
Done?
That’s it then? Model-based testing explained and we are ready to set of testing whatever comes our way? For simple scenarios and small nets then yes, but once complexity increases in terms of network size, non-determinism, asynchronous behavior and dependencies between data, maintaining an explicit model becomes cumbersome.
What follows next is conceptually simple but requires a lot of work to turn into a useful application. This is what I have done with the product Quality Gate One Studio and the rest of this article is to some extent specific for that tool.
Auto Generating P/T Nets
That’s it then? Model-based testing explained and we are ready to set of testing whatever comes our way? For simple scenarios and small nets then yes, but once complexity increases in terms of network size, non-determinism, data inter-dependencies and asynchronous behavior, maintaining an explicit model becomes cumbersome.
What follows next is conceptually simple but requires a lot of work to turn into a useful application. This is what I have done with the product Quality Gate One Studio and the rest of this article is to some extent specific for that tool.
Take a step back and consider what the P/T net consists of:
- Places
- Transitions
- Input arcs (arcs leading from a place to a transition)
- Output arcs (arcs leading from a transition to a place)
Then revisit my first article in the series that walks you through analytical test design and combinatorial test. The crux of this article is to apply categorization to the input parameters of a test method. The result being that each parameter to any given test belongs to exactly one category, or in P/T net terminology belongs to exactly one place. With this, we can pin three out of the four items a P/T net consists of:
- A Place corresponds to the category of a parameter in a single test
- A Transition corresponds to a test. That is, a binding between a test method and specific categories for each parameter.
- An Input Arc corresponds to the binding of a specific category (a Place) to one specific parameter of a test method.
That leaves the output arcs, but if it is possible to inspect an object (e.g. by using reflection) and determine what category / place it belongs to, if any, and it is possible to inspect what objects come out of a transition, then output arcs can be observed simply by executing transitions as they become enabled.
- An Output Arc corresponds to the place where an output of a transition ends up.
The discovery process proceeds as follows:
Initially no output arcs are known, but rank 0 transitions are by definition enabled. Firing these transitions provide enough information to identify rank 1:

The process continues like this until all transitions have been ranked or identified as dead:



Using Combinatorial Test Design to Define the Net
In the previous section, I explained how to discover output arcs by firing the transitions in rank order, but that saved less than half the work of setting up the network since places, input arcs and transitions remain. To nail these, consider the relationship between a test method and a transition. The test method is the code that calls the system under test and validates results, while the transition is just a binding between the method and a specification of parameter characteristics. If we can get the specification part into a compact form that expands into multiple transitions, we are done since places and input arcs are directly derivable from the transitions.
The first thing we need to do is to fix the representation of parameter categories and I choose to do this by adding Boolean and enum-type properties to the classes used for parameters in test methods. An example from the first article in the series is the abstract representation of a DateTime instance:
public class MDateTime
{
#region Category definitions
public enum YearCategory { Min, CommonYear, LeapYear, CommonCentury,
LeapCentury, Max }
public enum MonthCategory { Jan, Feb, Jun, Jul, Aug, Dec }
public enum DayCategory { First, SecondLast, Last }
public enum TimeCategory { Min, Mid, Max }
#endregion Category definitions
#region Factors
public YearCategory Year { get; set; }
public MonthCategory Month { get; set; }
public DayCategory Day { get; set; }
public TimeCategory Hour { get; set; }
public TimeCategory Minute { get; set; }
public TimeCategory Second { get; set; }
public TimeCategory Millisecond { get; set; }
#endregion Factors
…
}
If there is state involved like for the bug report example above, simply add another factor to represent the state and leave it to the test method to update the state as appropriate.
The class and the combined properties together, e.g. [Year.CommonYear, Month.Feb, Day.Last, …] defines the overall category of the object and hence the place where it belongs. The tuple / text representation is fine for the specification of input while the property representation lends itself well for reflection. Now there is sufficient information to represent the constituent parts of the P/T net, but a long list of explicitly defined tuples is not, in general, a compact representation. The solution I developed for Quality Gate One Studio is a general-purpose expression language supporting set operations, relational functions, Covering Arrays and more.
The net result being a system where you need to concern yourself with the following:
- Data modelling (mainly defining categories and factors)
- Implementing general purpose parameterized test methods
- Defining what to test.
The system then executes tests by observing output and doing dependency resolution as needed.

When you download QS there is a sample illustrating how to drive and test a stateful system.
Testing Asynchronous Systems
So far, the model has been synchronous and a transition is fired right away when it is selected for execution. To deal with asynchronous systems we need to support asynchronous execution. If you look at the code for the P/T net simulator, you will find a class called “Fixture” that represents a transition with a (partial) binding of parameters. The first step to support asynchronous execution is to use a queue to separate selection of fixtures and the execution of fixtures, next to provide a mechanism to put a fixture on hold until some event releases it.
What can put a fixture on hold? One option is to add a “ReadyAt” timestamp to the objects stored in the places of the P/T net. This facility supports the following scenario: Submitting an order (e.g. in a web shop) produces a separate email confirmation that arrives within two minutes. The solution is to let the transition submitting the order emit an “ExpectedEmail” object that is time-stamped to be ready two minutes after submitting the order. When the next transition that checks for emails, picks up the ExpectedEmail object, the related fixture goes on hold until it is ready.
This approach works only when the expected side effect is observable within the provided time frame and with only that mechanism at hand, you must use worst-case time frames to prevent false negatives in the test.
To speed things up we need a mechanism to provide normal-case time frames and a mechanism to retry the transition later if the first time frame was too optimistic. Thus, the second mechanism we need is the ability to retry a transition and put it back in the queue. In QS you can achieve that through a call to TestContext.TryLater().
The above provides the basis for polling and while it can support most asynchronous scenarios it complicates the test method code and has a rather clumsy feel.
Many asynchronous systems support completion callbacks. That is, calling a delegate supplied by the user when the asynchronous operation completes. To support this we need to be able to fire a transition (to set off the asynchronous operation), suspend it and resume it once we receive a completion callback. For QS I chose to support continuations which work as follows: Before the asynchronous operation is initiated, a delegate to the code to execute on completion (this is the continuation code such as validation code) is supplied to a method CreateContinuation() that returns another delegate to use as callback. When the callback is invoked, it passes any parameters to the continuation and releases the associated fixture. Continuations lead to more elegant user code and superior scheduling.
The above mechanisms support asynchronous operations initiated by firing a transition / calling a test method, but what about unsolicited events such as timer events or events from a live data feed? I have not found a good solution for this problem yet: It is simple enough to monitor for such events and add an object such as “NewsUpdate” to a place and then wait for a transition to consume the object and do its validation. The problem is that we do not know in advance the category of the received data, we do not know when we will receive the event, and if we monitor for multiple categories we do not know if we ever will receive data for all categories. Maybe that is just the way it is, but any thoughts on how to deal with it are most welcome!
Sometimes a transition is not fully deterministic. It emit output to different places on each call and it is not reliable to determine all output arcs from the transition. In this case, it is important to remember that only the dependency analysis needs deterministic output arcs. It is sufficient that the outputs go into the right places at run time, as long as there are sufficient deterministic output arcs that the dependency resolver can enable all transitions. For this reason, QS distinguishes between checked and unchecked output, where only the checked output must be deterministic.
If an output arc is strictly required for the dependency resolution but the transition is non-deterministic and sometimes provide the required output and sometimes not, it is possible for the test method to signal to QS whether the required output was available or not. In that case, QS can call the method again with new input until it observes the required output.
In this article, I have examined state-machines and P/T nets as models to drive a test. State machines respond poorly to complexity while P/T nets have better characteristics and provide some interesting opportunities. Introducing dependency resolution to the P/T net model enables us to pick any live transition (i.e. test case) and have the network decide the sequence of steps needed before it can execute. In integration scenarios, this means that you no longer need arrange code. Further, the dependency resolution enables sparse specification of load scenarios, again a lot easier to use than using traditional hardwired sequences. The type of sequence and load testing achieved using this technique is known as a Markov Chain Statistical Test (MCST). Compared to the common approach in MCST, with a P/T net with dependency resolution it is not necessary to specify all transition probabilities.
The attached code sample contains a P/T net simulator capable of MCST, but the raw model provided in the sample has scaling and maintenance issues and lacks support for asynchronous systems and non-determinism. I further discussed how the tool Quality Gate One Studio handles these issues by introducing formal test design techniques and leveraging these for automated discovery of network topology. This greatly improves scaling properties and makes both combinatorial testing, model-based testing and MCST available to systems of real life complexity.
I hope you enjoyed the article and that it provided you new insights and inspiration. For me, testing started as a rather dull chore that lead into a challenging journey across many different fields of Computer Science.
My next article in the series (and the last one so far) will be about performance testing, intricacies of high-speed timing, what statistics to use and what not, concurrency and more.
