An Optimal Wagner-Fischer Algorithm For Approximate Strings Matching In Python And NumPy

Arthur V. Ratz

5.00/5 (10 votes)

17 Sep 2022CPOL27 min read

11K

Compute the Levenshtein distance of literal strings effectively by using the Wagner-Fischer (two matrix rows-based) algorithm.

The Levenshtein distance is an efficient metric widely applied to evaluate the similarity between literal strings and other 1D sets. In this article, the optimal Wagner-Fischer algorithm for the Levenshtein distance computation and its implementation, are thoroughly discussed, by an example. The code samples in Python and NumPy demonstrate the similarity of literal strings evaluation, based on the Levenshtein distance and other metrics.

Download wfsch_levdist_numpy.zip - 224.4 KB

Introduction

"The notion of edit distance and the efficient algorithm for computing it have obvious applications to problems of spelling correction and may be useful in choosing mutually distant keywords in the design of a programming language." - R.A. Wagner, M.J. Fischer, MIT, Jan 1974.

Approximate string matching is a fundamental technique of many data analysis algorithms, providing an ability to determine the similarity between various textual data. Mostly, the similarity is numerically represented in terms of distance between two literal strings.

The approximate string matching finds its application in spell checker and word autocomplete features of many existing web and mobile applications, providing the correct word suggestions for word typos or other incorrect user inputs. The full-text search engine of a spell checker computes the distance between the user input and each of the correct strings in its database, finding the most similar words, the distance of which is minimal.

The various classical distance metrics, such as Sørensen’s index and Hamming distance, are applied to determine the similarity of textual data. However, using these metrics eventually leads to incorrect suggestions, caused by the misleading distance between those similar strings computation. Applied to the literal strings, the Hamming distance and other metrics are not aware of common substrings (suffixes) and the adjacent character transpositions, evaluating the largest distance between the most similar strings.

It was proved by Vladimir Levenshtein, in 1965, that it’s possible to evaluate the distance between strings, as the minimal number of such single-character editing operations, required to transform a distorted string into the correct one. The Levenshtein distance metric was formulated as the Levenshtein automata algorithm. It was used as an alternative to the Hamming codes, for restoring the correct bytes from damaged or distorted binary streams.

The Levenshtein distance is a very popular data analysis algorithm, used for a widespread of applications, completely solving the problem of textual data similarity evaluation, aware of common substrings and adjacent character transpositions.

There is an entire class of algorithms to compute the Levenshtein distance, including two variations of the Wagner-Fischer algorithm, and the Hirschberg algorithm to evaluate the similarity and optimal strings alignment, introduced by D.S. Hirschberg, in 1975.

An optimal Wagner-Fischer (two matrix rows-based) algorithm and its implementation are thoroughly discussed in this article. The code samples in Python demonstrate using the Wagner-Fischer algorithm to compute the Levenshtein distance of various strings, in the University of Michigan’s “An English Word List” dataset (https://www-personal.umich.edu/~jlawler/wordlist.html), consisting of over 60K English words, alphabetically sorted.

The Levenshtein Distance

The Levenshtein distance is a metric for an effective distance and similarity of two literal strings evaluation. It solely relies on representing the distance as a minimal count of editing operations, made to the first string, transforming it into the second one, rather than the statistics of characters unmatched in both strings.

Obviously, one string is transformed into another string via a series of deletions, insertions, and replacements of characters in the first string. As the result, two dissimilar strings are being transformed by using a large number of edits, and the most similar ones – with the lesser number of such edits, respectively.

The main benefit of the Levenshtein distance is that the similarity of strings is evaluated, observing that both strings might have a common substrings, and thus, the correct distance between such strings is actually smaller than the Hamming or other distances. Also, the Levenshtein distance is evaluated, solely based on obtaining the counts of characters that are to be deleted, inserted, or replaced, without performing the strings transformation, itself.

In the case when, two strings don’t have common substrings (suffixes), the Levenshtein and Hamming distances are the equal. Otherwise, the Levenshtein distance is computed, aware of the common substrings, the positions of which have not been matched in both strings, since it’s only possible to evaluate the distance of such strings as the minimal edits count of their transformation.

The Levenshtein distance between two full strings, $a$ and $b$ of different lengths, $|a|$ and $|b|$, is given by the recurrence piecewise function $\mathcal{Lev}(a,b)$, listed below:

$\mathcal{L}(a,b) = \begin{cases} |a| &\text{, if } |b| = 0\\ |b| &\text{, if } |a| = 0\\ \mathcal{L}(tail(a),tail(b)) &\text{, if } a[0] = b[0]\\ min \begin{cases} \mathcal{L}(tail(a),b) &\text{deletion}\\ \mathcal{L}(a,tail(b)) &\text{insertion}\\ \mathcal{L}(tail(a),tail(b)) &\text{replacement}\\ \end{cases} &\text{, otherwise} \end{cases}$

Here, the distance of the two strings computation basically deals with the string tails, $\textbf{tail}(a)$ and $\textbf{tail}(b)$. A $\textbf{tail}(a)$ is a string of all characters, except for the first character of the string $a$. For example: obtaining each next i-th $\textbf{tail}(a)$ results in a new string, containing all remaining characters from $a$, followed by the $a[i]$ character. Matching the $\textbf{tail}(a)$ to the string $b$ , at the positions of the first characters, causes 1-deletion of a single character from the beginning of the string $a$. Similarly, 1-insertion of a character to the end of the string $a$ is made by matching the string $a$ to the $\textbf{tail}(b)$, correspondingly. As well, 1-replacement of the $a[0]$ with $b[0]$ characters is done, proceeding to the first characters of the next $\textbf{tail}(a+1)$ and $\textbf{tail}(b+1)$ strings. The specific edits are done by hovering one of these strings, $a$ or $b$, or both, aligned to the first characters position in both strings, so that each of these alignments leads to the string $a$ into $b$ transformation.

While computing the Levenshtein distance recursively, the piecewise function handles the cases when the first characters are equal, not equal, or one of the string lengths, $|a|$ or $|b|$, equals to $0$. The computation starts at the first characters $a[0]$ and $b[0]$. If the characters $a[0]$ = $b[0]$, are equal, it proceeds to the next pair of the $\textbf{tail}(a+1)$ and $\textbf{tail}(b+1)$ strings, because none of such edits is required when the first characters of $\textbf{tail}(a)$ and $\textbf{tail}(b)$ are equal and matched at their positions. Otherwise, if $a[0]$ != $b[0]$, the same piecewise function $\mathcal{Lev}(a,b)$ is recursively applied to each of the strings, $\mathcal{Lev}(\textbf{tail}(a),b)$, $\mathcal{Lev}(a,\textbf{tail}(b))$, $\mathcal{Lev}(\textbf{tail}(a),\textbf{tail}(b))$, respectively. The distance computation for each pair of these strings proceeds until the equal first characters, $a[0]$ and $b[0]$, have been finally matched. The piecewise function, recursive called, accumulates the counts of deletions, insertion, and replacements of characters in a, incrementing the corresponding edit counts by $1$. The Levenshtein distance between the $\textbf{tail}(a)$ and $\textbf{tail}(b)$ strings is evaluated as the minimal of such counts. It proceeds the distance computations, starting at those tails, for which the count of edits is the smallest. In the case when one of the string lengths, $|a|$ or $|b|$, is $0$, the piecewise function returns the non-zero length, since the $a$ to $b$ string transformation requires the remaining characters to be inserted into the string $a$, which number is equal to the length of a non-empty string. Finally, when the lengths of both strings, $a$ and $b$, are equal to $0$, the computation ends, and the value of the piecewise function $\mathcal{Lev}(a,b)$ is the Levenshtein distance of full strings $a$ and $b$, being evaluated.

The Levenshtein piecewise function has one straightforward implementation in most programming languages, Haskell, Python, etc. However, it incurs the growing recursion depth caused by the distance of the same substrings re-computation, and thus, cannot be effectively used as a computational algorithm.

An Optimal Wagner-Fischer Algorithm

A better Levenshtein distance algorithm was devised by R. A. Wagner and M. J. Fischer, in 1974. It computes the Levenshtein distance of two full strings, $S_{1}$ and $S_{2}$, based on the matrix M, that holds the minimal distances $M[i][j]$ between each $i$-character prefix of $S_{1}$ and each $j$-character prefix of $S_{2}$, correspondingly. The Wagner-Fischer algorithm is a dynamic programming algorithm, in which the Levenshtein distance computation is divided it into multiple sub-problems, computing the same minimal distances between the prefixes (i.e., “smaller” substrings) of the $S_{1}$ and $S_{2}$ strings.

This algorithm basically deals with pairs of the $i$- and $j$-character prefixes, $S_{1}[0..|i|]$ and $S_{2}[0..|j|]$, of both strings, rather than suffixes or string tails. Specifically, the $i$-character prefix of a string $S$ is an initial segment of the $S[i]$-character, followed by the first $i$-characters of the string. The $i$- and $j$-character prefixes of the $S_{1}$ and $S_{2}$ strings are shown in the figure, below:

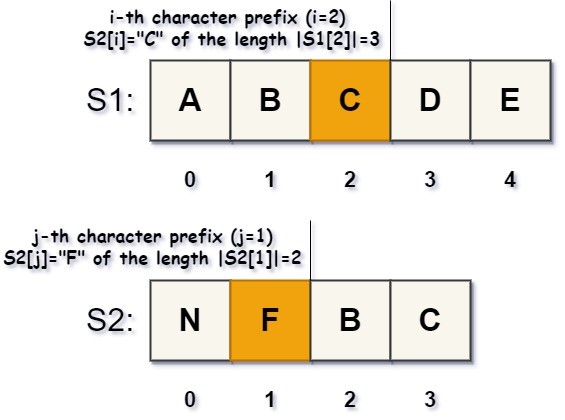
A prefix length $|i|=i+1$ is the count of the first $i$-characters of $S$, including the prefix character $S[i]$. As well, an “empty” 1-character prefix ( # ) is inserted at the positions of the first characters $S_{1}[0]$ and $S_{2}[0]$ in both strings.

S₁ To S₂ String Transformation

Similar to the Levenshtein recurrence piecewise function, the Wagner-Fischer algorithm computes the Levenshtein distance, based on the deletion, insertion, and replacement counts of each prefix $S_{1}[i]$ into $S_{2}[j]$ transformation.

Logically, each of these editing operations are a bit different than usually:

Deletion from S₁, Insertion to S₂: the number of characters is deleted from the beginning of the $S_{1}$ string, inserting it to the end of the string $S_{2}$. This number is the deletions count of the $S_{1}[i]$ into $S_{2}[j]$ transformation:

If the length $|i|$ is less than $|j|$, which is $|i| < |j|$, the prefix $S_{1}[i]$ cannot be transformed into $S_{2}[j]$ via a series of insertions, which count is equal $0$. Since then, to find the minimal edit distance of the $S_{1}[i]$ into $S_{2}[j]$ transformation, the previous minimal distance is used.

Insertion to S₁, Deletion from S₂: the insertions of characters to $S_{1}$ are made by deleting each of the characters, including the empty prefix ( # ), from the beginning of $S_{2}$, and appending it to the end of $S_{1}$. The insertion count is the number of characters being inserted to $S_{1}$ and deleted from $S_{2}$, correspondingly:

Likewise, when the length $|i|$ of the prefix $S_{1}[i]$ is greater than the $S_{2}[j]$ prefix length $|j|$, which is $|i| > |j|$, the prefix $S_{1}[i]$ cannot be transformed into $S_{2}[j]$ via the insertion edits, and its count equals to $0$. The distance $M[i][j]$ of such transformation is obtained based on one of the previous distances in the matrix M, instead.

Replacement of S₁[i] with S₂[j]: the replacements are made only if the positions of characters $S_{1}[i]$ and $S_{2}[j]$ have been matched, $i = j$, in both strings. In this case, the replacements count is the number of such deletions or insertions to $S_{1}$, that the characters $S_{1}[i]$ and $S_{2}[j]$ have been finally occurred at the same positions in $S_{1}$ and $S_{2}$, respectively. If the characters $S_{1}[i]\neq{S_{2}[j]}$, are not equal, at their equal positions, $1$ is added to the deletions or replacements count, since 1-replacement of the character $S_{1}[i]$ with $S_{2}[j]$ has been made.

The Distance Values Stored In The Matrix M

The Levenshtein distance between strings $S_{1}$=ABCDE and $S_{2}$=NFBC computation yields the distance matrix M of shape $(5\times{4})$, shown below:

The distance values in the matrix $M$ are arranged in such a way that each i-character prefix $S_{1}[i]$ is mapped onto all corresponding j-character prefixes $S_{2}[j]$, and the values $M[i][j]$ are the distances between corresponding prefixes, respectively. The values in the first $0$-th column and $0$-th row of the matrix are the minimal distances (red) between an empty string ( # ) and each of the prefixes $S_{1}[i]$ or $S_{2}[j]$. Since the first character ( # ) is inserted at the beginning of both strings, the positions of characters in $S_{1}$ and $S_{2}$ – zero-based, and the prefix indexes in $M$ are one-based.

There are three basic kinds of distances stored in the matrix$M$, which values of which are the characters deletion, insertion, and replacement counts of the corresponding prefixes, $S_{1}[i]$ and $S_{2}[j]$, transformation. The deletion counts are the values (dark grey) below the matrix diagonal, and the insertion counts - the values (light grey) above its diagonal, as well as, the replacement counts are the values (green) along the matrix \$M$ diagonal, respectively.

Initialization

The Wagner-Fischer algorithm solely relies on the observation that the Levenshtein distance bottom-top computation is only possible, in the case when the distances from an “empty” string, $S_{1}$ or $S_{2}$, to all of the prefixes of another string, are initially provided. Each of these distances is the count of characters that must be deleted from or inserted into an empty string ( # ), $S_{1}$ or $S_{2}$, transforming it into the $S_{2}[j]-$ or $S_{1}[i]$-prefix, correspondingly.

Since then, the 1st column of $M$ is assigned to the distances, $M[0..|S_{1}|)[0] = 0,1,2,3,...,|S_{1}|$, between each $S_{1}[i]$-prefix and the empty $S_{2}$ = ( # ) string. Each of these distances is the count of characters deleted from the prefix $S_{1}[i]$, so that it’s finally transformed to the empty string ( # ). Obviously, such count of deletions is the length $|i|$ of the $S_{1}[i]$-prefix, initially provided. Similarly, the 1st row of $M$ is initialized with the distances $|j|$, $M[0][0..|S_{2}|) = 0,1,2,3,...,|S_{2}|$, from the empty string $S_{1}$ = ( # ) to each of the $S_{2}[j]$-prefixes, correspondingly.

Levenshtein Distance of S₁ and S₂ Computation

Once the distance matrix $M$ of shape $(|S_{1}|\times{|S_{2}|})$ has been already defined, it computes the Levenshtein distance, row-by-row, filling each $i$-th row of $M$, with the distances from the $i$-th character prefix, $S_{1}[i], i=[1..|S_{1}|) $, to each of the prefixes $S_{2}[j], j=[1..|S_{2}|) $, until the last distance value $M[|S_{1}| - 1][|S_{2}| - 1]$ is finally the Levenshtein distance of the $S_{1}$ and $S_{2}$ full strings. The distance $M[i][j]$ between the corresponding prefixes, $S_{1}[i]$ and $S_{2}[j]$, computation is given by the expression:

$M[i][j] = min \begin{cases} M[i-1][j] + 1 &\text{, deletion}\\ M[i][j-1] + 1 &\text{, insertion}\\ M[i-1][j-1]+1_{(S1[i]\neq{S2[j]})} &\text{, replacement}\\ \end{cases}$

The expression, above, evaluates the distance $M[i][j]$ of prefixes $S_{1}[i]$ and $S_{2}[j]$, calculating the minimal of the distances, previously computed for the other prefixes. Each of these distances exactly corresponds to the counts of deletions, insertions, and replacements, made to the $S_{1}$ string:

$M[i-1][j] + 1$	Deletion from S₁, Insertion to S₂
$M[i][j-1] + 1$	Insertion to S₁, Deletion from S₂
$M[i-1][j-1] + 1_{(S_{1}[i]\neq{S_{2}[j]})}$	Replacement of S₁[i] with S₂[j]

The Levenshtein distance computation starts at the distance value $M[1][1]$ of the first prefixes $S_{1}[1]$ and $S_{2}[1]$ of both strings, applying the expression, above, to all combinations of the $S_{1}$ and $S_{2}$ prefixes, until the distance $M[|S_{1}| - 1][|S_{2}| - 1]$ between the longest prefixes has been finally computed and is the Levenshtein distance, being evaluated.

According to the dynamic programming approach, the matrix $M$ is split into multiple “small” sub-matrices of the shape $(2\times{2})$. The values of each sub-matrix are the counts of characters deleted $M[i-1][j]+1$ (red), inserted $M[i][j-1]+1$ (blue) and replaced $M[i-1][j-1]+1$ (green):

The distance $M[i][j]$ between each of the prefixes, $S_{1}[i]$ and $S_{2}[j]$, is computed as the minimal of those counts, above. The value $M[i][j]$ in the last sub-matrix is the Levenshtein distance, being evaluated.

Finally, an average-case complexity and space used by the Wagner-Fischer algorithm are $\theta(|S_{1}|\times{|S_{2}|})$, although more optimal variations of the algorithm exist.

Iterative Two Matrix Rows Algorithm

However, the same Levenshtein distance might be evaluated without the full distance matrix M computation. Each of the prefixes, $S_{1}[i]$ and $S_{2}[j]$, distance computation is based solely on the values of the current i-th and previous (i-1)-th rows of the matrix, and thus, the values in the other rows can be simply discarded. It provides an ability to significantly reduce the space used by the algorithm to O(2 x |S_{2}|).

The pseudo-code of the Wagner-Fischer (two matrix rows) algorithm is listed below:

\( \textbf{algorithm }\text{Wagner-Fischer}(S_{1},S_{2})\textbf{ is:}\\ \hspace{28pt} \textbf{declare: } \textrm{V}_{old}[0..|S_{2}|) = \{0\} \textbf{ as } \textrm{integer}\\ \hspace{73pt} \textrm{V}_{new}[0..|S_{2}|) = \{0\} \textbf{ as } \textrm{integer}\\\ \\ \hspace{28pt} \textbf{output: } \mathcal{L} - \textit{the Levenshtein distance of }S_{1}\textit{ and }S_{2}\\\ \\ \hspace{28pt} \textbf{Initialize: } \textrm{V}_{old}[0..|S_{2}|) \textit{ vector with the "insertion" distances }\\ \hspace{85pt} \textit{from the 1-prefix (#) to each of the prefixes }S_{2}[0..|j|), j=[0..|S2|)\\ \hspace{28pt} \textbf{for each } \textit{i} \in{ [0..|S_{1}|)} \textbf{ do: } \textrm{V}_{old}[i] = i\\\ \\ \hspace{28pt} \textbf{for } \textit{i} \gets{1} \textbf{ to } |S_{1}| \textbf{ do: }\\ \hspace{46pt} \textrm{V}_{new}[0] = i;\\ \hspace{43pt} \textrm{V}_{new}[1..|S2|) = 0\\ \hspace{46pt} \textbf{for } \textit{j} \gets{1} \textbf{ to } |S_{2}| \textbf{ do: }\\ \hspace{65pt} \textit{rCost} = 1 \textbf{ if } S_{1}[i-1]\neq{S_{2}[j-1]} \textbf{ else: } 0 \\ \hspace{65pt} \textit{del} = \textrm{V}_{old}[j] + 1\\ \hspace{65pt} \textit{ins} = \textrm{V}_{new}[j - 1] + 1\\ \hspace{65pt} \textit{rep} = \textrm{V}_{old}[j - 1] + \textit{rCost}\\\ \\ \hspace{65pt} \textrm{V}_{new}[j] = \textbf{minimum}(del,ins,rep)\\\ \\ \hspace{46pt} \textrm{V}_{old} \gets{\textrm{V}_{new}}\\\ \\ \hspace{28pt} \mathcal{L} \gets{V_{old}[|S_{2}|-1]}\\\ \\ \hspace{28pt} \textbf{returns: } \mathcal{L} \)

This algorithm declares two vectors $V_{old}$ and $V_{new}$, denoted as e_d and e_i in the specific Python code sample, discussed below. The vector $V_{old}$ is initialized with the count of characters that must be inserted into the empty $S_{1}$ string ( # ), transforming it into the string $S_{2}$

For each i-th prefix $S_{1}[i], i=[1..|S_{1}|)$ it initializes the second vector $V_{new}$, assigning the first values $V_{new}[0]$ to the count of characters deleted from $S_{1}$ to transform it into the empty string ( # ) $S_{2}$, while all other values of the $V_{new}$ vector are initially 0s. At each iteration, it computes the distances $V_{new}[j]$ between the i-th prefix $S_{1}[i]$ and all prefixes $S_{2}[j], j=[1..|S_{2}|)$, stored in the $V_{new}$ vector. Since all of these values in $V_{new}$ have already been computed, it updates the vector $V_{old}$ with the values, copied from the $V_{new}$ vector, proceeding to the distances computation for all next $(i+1)$-th prefixes $S_{1}[i+1]$, until the distances from the final prefix $S_{1}[|S_{1}|-1]$ have been computed. The last value in the corresponding $V_{new}[|S_{2}|-1]$ vector is the Levenshtein distance of the full $S_{1}$ and $S_{2}$ strings.

An Example...

Suppose a distorted and the correct strings are $S_{1}$ = ADVBBR and $S_{2}$ = ADVERBS, respectively. The distorted $S_{1}$ and the correct $S_{2}$ strings both have the equal prefix ADV… . As well, the adjacent characters R, B of $S_{2}$ have been transposed, B, R, in the distorted string $S_{1}$, and the distorted string $S_{1}$ is missing characters, E and S, from the correct $S_{2}$ string:

The Levenshtein distance of the $S_{1}$ and $S_{2}$ full strings evaluation starts with the corresponding character prefixes $S_{1}[1]= S_{2}[1] =$ A of both strings, and the minimal edit distance $M[1][1]$ is computed. Since both prefixes A are same, and are matched at the same position in $S_{1}$, none of the replacements is made, and its count equals to $0$. Otherwise, the replacements count is $1$, when the first character prefixes of both strings are not the same, $S_{1}[1]\neq{S_{2}[1]}$, and 1-character replacement of $S_{1}[1]$ with $S_{2}[1]$ is to be made. Here, the prefix A is followed by another “empty” prefix ( # ), and the single-character deletion and insertion to $S_{1}$ is required to change the prefix, A to ( # ), and ( # ) to A, in the either $S_{1}$ or $S_{2}$ string, respectively. Since the deletion, insertion, and replacement counts are initially provided, the computation of these counts is not basically required. Finally, the minimal of these counts is the distance value $M[1][1] = min(1,1,0) = 0$, in the case when the first prefixes, $S_{1}[1] = S_{2}[1]$, are equal, and $M[1][1] = min(1,1,1) = 1$, unless otherwise:

Next to the prefix A of $S_{2}$, the minimal edit distance $M[1][2]$ for the prefixes $S_{1}[1]$ = A and $S_{2}[2]$ = D is computed.

Here, the insertions count is equal to $2$, since 2-insertions (blue) of the characters ( # ), A, deleted from $S_{2}$, is required to match the characters A and D at the same position of A in $S_{1}$:

As well, the replacements count of the character A with D equals to $1$, because only 1-insertion to the end of $S_{1}$ should be made to change the prefix A to D in $S_{1}$:

In this case, there’s no deletions count for the prefixes A and D, since it’s impossible to transform A into D, via a series of deletions from $S_{1}$. Since then, the count of deletions is the minimal edit distance $M[1][1]$ = $0$, between the equal prefixes A, previously obtained:

Finally, $1$ is added to the deletion, insertion, and replacement counts, observing the empty prefix ( # ) length, and the minimal edit distance $M[1][2]$ between those prefixes A and D is obtained as the minimal of such counts, which is $M[1][2] = min(1,3,2) = 1$.

The same method is applied to the next minimal distance $M[1][3]$, of the prefixes $S_{1}[1] = $ A and $S_{2}[3] =$ V, computation.

Here, the deletion, insertion, and replacement counts are equal to 1, 3, and 2, respectively. Obviously, the A into V transformation requires 3-insertions of the characters, ( # ), A, D to $S_{1}$. As well, 2-deletions of the characters A, and D from $S_{2}$ should be made to replace the prefix A with V. Finally, the minimal distance between A and V evaluates to $M[1][3] = min(2,4,3) = 2$:

The minimal distances between the prefix A of $S_{1}$ and each of the next prefixes E,R,B,…,S of $S_{2}$, are computed, until the minimal distance $M[1][7] = 6$ of the A and S prefixes has been finally obtained.

Likewise, the distances between the next prefix D of $S_{1}$ and all corresponding prefixes A,D,V,…,B,S of $S_{2}$, in the 2nd row, are computed, based on the minimal distances between other prefixes in the 1st row of $M$, previously obtained.

For example, the minimal edit distance $M[2][1]$ between $S_{1}[2]$ = D and $S_{2}[1]$ = A prefixes is the minimal of the corresponding distances between (A, #), (D, #), and (A, A) prefixes of $S_{1}$ and $S_{2}$. Normally, it requires 2-deletions of the characters #, A from $S_{1}$, as well as the only 1-replacement of A with D, by appending the first character A from $S_{1}$ to the end of $S_{2}$, deleting it from $S_{1}$, such as:

Here, the count of characters deleted from $S_{1}$ is also the minimal distance $M[2][0]$ between prefixes (D, #), in the previous 1st row, because 2-deletions of the #, A characters must be done in both cases. As well, the replacements count is equal to the minimal distance between (A, #), since the transformation of D into A relies on the previous A to ( # ) prefixes transformation. In this case, the replacements count is $1$, since the only 1-character A has been deleted from $S_{1}$ and inserted to $S_{2}$, matching the D and A prefixes at the same positions in $S_{1}$ and $S_{2}$, correspondingly. Finally, there’s neither such the prefix D to A transformation via the insertion of characters to $S_{1}$, nor deletions or replacements of characters are to be made in $S_{1}$. That’s why, the insertions count for this transformation is $0$:

Since then, the minimal distance $M[2][0]$ between the prefixes D and A is $M[2][0] = min(3,1,2) = 1$.

The minimal distance $M[2][2]$ between the equal prefixes $S_{1}[2]$ = D and $S_{2}[2]$ = D is equal to $0$. This distance $M[2][2] = 0$ is evaluated similarly to the A and A prefixes distance, previously discussed, above:

Here, the minimal distance $M[2][3]$ between the prefixes $S_{1}[2]$ = D and $S_{2}[3]$ = V is the point of a special interest.

The transformation of D into V prefixes via the insertions to $S_{1}$ incurs the previous transformation of A into V, made by replacing the prefix A with D. The replacement of A with D is done by inserting the character A to $S_{1}$, deleted from $S_{2}$. Here, the count of insertions for the A and D prefixes is $1$, and the minimal distance $M[1][1]$ of the A into V transformation is $2$, respectively. Thus, the insertions count for the D into V transformation is equal to the minimal distance $M[1][1]$ between A and V, which is $2$:

In turn, the replacements count of the D into V transformation is also the minimal edit distance $M[1][2]$ between the A and D prefixes, because the prefix A cannot be transformed into D via the deletions from $S_{1}$, as well as the prefix D of $S_{1}$ is followed by the equal prefixes ( # ) and A, matching the same positions in $S_{1}$ and $S_{2}$. Here, the count of insertions and deletions, transforming prefixes ( # ) into A, and A into ( # ), is $1$, and the replacements count for the equal prefixes A is $0$. Obviously, the minimal distance between the prefixes A and D is $M[1][2] = min(2,2,1) = 1$. Finally, the replacements count for the D into V transformation is $1$:

Similarly, the deletions count for the D and V prefixes is the minimal edit distance $M[2][2]$ of the equal prefixes D and D transformation, because it’s impossible to transform D into V by deleting the characters from $S_{1}$, and the prefixes D are both same at their positions in $S_{1}$, $S_{2}$. As the result, the replacements count, equal to $0$, which is both the minimal edit distance of D into D transformation and the deletions count for the D and V prefixes, correspondingly. According to this, the minimal edit distance $M[2][3]$ is obtained as the minimal of the edit counts, discussed above, $M[2][3] = min(1,3,2) = 1$:

The computation, discussed above, proceeds to all remaining distances in the matrix $M$, until the last minimal distance $M[6][7]$ between the $S_{1}[6] =$ R and $S_{2}[7]$ = S prefixes has been finally obtained, based on all previous minimal distances observation. The minimal edit distance $M[6][7]$ is the Levenshtein distance of the $S_{1}$ and $S_{2}$ full strings, which is equal to $3$:

Finally, the Levenshtein distance of $S_{1}$ and $S_{2}$ can be evaluated without computing the full matrix $M$, because the minimal distances from the $i$-character prefix of $S_{1}$ and all $j$-character prefixes of $S_{2}$, in each $i$-th row, are obtained, based on the values in the $(i-1)$-th row of the matrix, only. The distance values in the other previous rows are not used for such computations, and thus, are simply discarded.

The Levenshtein Distance To The Similarity Score Conversion

For many applications, the Levenshtein distance between the $S_{1}$ and $S_{2}$ strings must be converted to the similarity score value in the interval $[0;1]$. The similarity score is computed based on the Hamming distance of the $S_{1}$ and $S_{2}$ strings, normalized to the same interval of $[0;1]$. Since the Hamming distance $D_{h}$ is always an upper bound of the Levenshtein distance $\mathcal{Lev}(S_{1},S_{2})$, it’s easy to calculate the similarity score $S_{L}$, representing the Levenshtein distance in the interval $[0;D_{h})$, rather than $[0;1]$.

There are several steps to the similarity $S_{L}$ value, such as:

1. Compute the Hamming distance $D_{h}$ between the $S_{1}$ and $S_{2}$ strings.

2. Normalize the distance $D_{h}$ to the interval $[0;1]$ using the formula, below:

$H_{norm} = \frac{D_{h}}{max\{|S_{1}|,|S_{2}|\}}$

3. Calculate the similarity score $S_{L}$, representing the Levenshtein distance $\mathcal{Lev}(S_{1},S_{2})$ in the interval $[0;D_{h})$:

$S_{L} = 1.0 - \frac{\mathcal{Lev}(S_{1},S_{2})\times{H_{norm}}}{D_h}$

In the formula, above, the distance $\mathcal{Lev}(S_{1},S_{2})$ is multiplied by the normalized value $H_{norm}$, dividing it by the Hamming distance $D_{h}$, and subtracting from $1.0$.

Here, the Levenshtein distance between $S_{1}$ and $S_{2}$ is normalized by using the classical min-max normalization formula. Finally, the largest Levenshtein distances $\mathcal{Lev}(S_{1},S_{2})$ correspond to the smallest similarity score $S_{L}$, and vice versa.

Using the code

A function, implementing the optimal Wagner-Fischer algorithm in Python 3, using NumPy, is listed below. The d_lev(s1,s2,c=[],dtype=np.uint32) function computes the Levenshtein minimal edit distance of two strings s1 and s2 of different lengths, len(s1) != len(s2). The deletion, insertion, and replacement costs are all equal to 1, (e.g., c = [1,1,1]), when the array of costs c is not defined:

Python

def d_lev(s1,s2,c=[],dtype=np.uint32):
    
    # Initialize the vector e_d[0..|s2|] with the minimal edit distances |j|, 
    # between s1[0] (i.e., the prefix '#') and each of the s2[j], j=[0..|s2|) prefixes.
    e_d = np.arange(len(s2) + 0, dtype=dtype)

    # If s1 equals to s2, the mininal edit distance is 0
    if s1 == s2: return 0
    # If c is undefined, all edit costs are 1 (default)
    if c is d_lev.__defaults__[0]: 
       c = np.ones(3, dtype)

    # Compute the minimal edit distances for all combinations 
    # of prefixes s1[i] and s2[j] as the minimal of distances between the other prefixes. 
    for i in np.arange(1,len(s1)):

        # Initialize the "insertions" vector e_i[0..|s2|), in which
        # the first element e_i[0] is the prefix length |i| of s1, 
        # and all other elements e_i[1..|s2| + 1] are zeros:
        e_i = np.concatenate(([i], np.zeros(len(s2) - 1, dtype)), axis=0)

        for j in np.arange(1,len(s2) + 0):

            # Get the replacement cost for the prefixes s1[i],s2[j]:
            # The r_cost is 0 if the s1[i] and s2[j] are the same, 
            # and is equal to 1, unless otherwise
            r_cost = 0 if s1[i - 1] == s2[j - 1] else 1
            
            # Evaluate the distance between s1[i] and s2[j] as the minimal of the deletion, 
            # insertion, and replacement counts of the s1[i] into s2[j] transformation
            e_i[j] = np.min([ \
               (e_d[j] + 1) * c[0],           # s1[i] - deleted from s1, and inserted to s2
               (e_i[j - 1] + 1) * c[1],       # s2[j] - inserted to s1, and deleted from s2
               (e_d[j - 1] + r_cost) * c[2]]) # s1[i] - replaced by s2[j]

        # Copy the current "insertions" vector e_i to the "deletions" vector e_d.
        # The e_i and e_d vectors are not necessary to be swapped.
        e_d = np.array(e_i, copy=True)

    # The Levenshtein distance e_d[|e_d|-1] between s1 and s2
    return e_d[len(e_d) - 1]

The code, listed above, uses two vectors (rows) e_d and e_i of the length |s2|, to hold the "deletion" and "insertion" counts. The vector e_d is initialized with the absolute counts of insertions, required to transform an empty prefix s1[0] = # to each of the s2[0..|s2|) prefixes: e_d=[0, 1, 2, 3,..., |s2|]. Also, the vector e_i is initialized, at each iteration, assigning the prefix length |i| as its first value, e_i[0]=|i|, while all other values are set to e_i[1..|s2|] = 0. For each pair of s1[0..|i|], i=[1..|s1|) , and s2[0..|j|], j=[1..|s2|) prefixes, it computes the minimal of the "deletion", "insertion", or "replacement" counts, based on the Levenshtein distance formula, applied to the previous distances in the e_d and e_i vectors, correspondingly. The new values are stored in the vector e_i, and the values of the e_d vector are updated by copying the new e_i vector to e_d. At the end of this computation, the last value in the e_d vector is the Levenshtein distance between strings s1 and s2.

I've also implemented the other distance metrics, such as Sørensen's index and the Hamming distance. The fragment of code, listed below, implements Sørensen's index computation:

Python

def sorensen_score(s1,s2):
    # The Sorensen's index value is equal to 1 if s1,s2 are equal
    if s1 == s2: return 1.0

    # The unique characters from the arrays s1 and s2
    s1 = np.unique(np.asarray(list(s1)))
    s2 = np.unique(np.asarray(list(s2)))
    
    # Computes the count of characters in the intersection of s1 and s2,
    # divided by the length of the largest string, and multipled by 100%
    return np.multiply(100, \
        np.divide(np.size(np.intersect1d(s1,s2)), \
                  np.max((np.size(s1),np.size(s2)))))</span>

The Sørensen's index value is trivially computed as the count of equal characters, in the intersection of the s1 and s2 strings, divided by the size of the longest string.

Another fragment of code, listed below, implements the Hamming distance metric:

Python

def hamming_dist(s1,s2):
    
    # The distance is 0 if s1,s2 are equal
    if s1 == s2: return 0

    # arrays of characters s1,s2
    s1 = np.asarray(list(s1))
    s2 = np.asarray(list(s2))

    # l_diff - the difference of the s1,s2 lengths
    l_diff = abs(np.size(s1) - np.size(s2))

    # l_min - the smallest of s1,s2 lengths
    l_min = np.min((np.size(s1),np.size(s2)))
    
    # The arrays s1,s2 are justified to the length of a shortest string, s1 or s2.
    # Hamming distance is the count of those characters, are not the same at 
    # their positions in the s1 and s2 arrays
    return np.count_nonzero(s1[:l_min] != s2[:l_min]) + l_diff

To evaluate the Hamming distance between strings s1 and s2 of different lengths, the smallest of the s1 and s2 lengths l_min and the difference in their lengths l_diff are obtained. Then, the longest strings, s1 or s2, is truncated to the length of the shortest one, such as that s1[:l_min] and s2[:l_min]. It applies a search to get the count of positions, at which the characters of s1 and s2 are not equal. The Hamming distance value is evaluated as the count of such positions, incremented by the l_diff value, and returned from the function.

Here are also a couple of code fragments, converting the Hamming and Levenshtein distances to the strings similarity score.

The Hamming distance is converted by normalizing its value to the interval $[0..1]$. A fragment of code, below, demonstrates such a computation:

Python

def hamm_score(s1,s2,d):
    # The similarity score is 1 if s1,s2 are equal
    if s1 == s2: return 1.0

    # Divide the Hamming distance by the length of the 
    # largest of s1,s2 strings, subtracted from 1.0
    return 1.0 - d / np.max((len(s1),len(s2)))

The resultant similarity score is $1.0$ if the strings s1 and s2 are identical. Otherwise, the Hamming distance d is divided by the largest of the len(s1) and len(s2) lengths, representing the distance in the interval of $[0..1]$. The strings, for which the distance value is the smallest, are the most similar. That's why the normalized distance value is subtracted from $1.0$ to obtain the correct similarity of the s1 and s2 strings.

The conversion of Levenshtein distance into the similarity score is just a bit different. An upper bound of the Levenshtein distance is the same Hamming distance value. Since then, the Levenshtein distance is normalized within the interval of $[0..D_{h}]$, rather than $[0..1]$, as shown in the code fragment, below:

Python

def lev_score(s1,s2,dl):
    # The similarity score is 1 if s1,s2 are equal
    if s1 == s2: return 1.0
    # Compute the Hamming distance of the s1,s2 strings
    dh = hamming_dist(s1,s2)
    # Normalize the Hamming distance in the interval [0,1]
    h_norm = dh / np.max((len(s1),len(s2)))
    # Multiply the Levenshtein distance of s1,s2 by the Hamming similarity score,
    # divided by the Hamming distance, and subtacting it from 1.0
    return 1.0 - dl * h_norm / dh

To get the similarity score, the Hamming distances dh of the s1 and s2 strings are obtained. Then both the Levenshtein and Hamming distance, dl and dh, are normalized in the same interval of $[0..1]$. The Levenshtein distance value is represented in the interval of $[0..D_{h}]$, as the product of the Levenshtein dl and normalized Hamming distance h_norm, divided by the Hamming distance dh, subtracting it from $1.0$.

Alongside the implementation of the optimal Wagner-Fisher algorithm, I've additionally developed a code, demonstrating the Levenshtein distance and similarity score computation for a variety of strings, stored in the strings.txt file, surveying the efficiency of the Levenshtein distance and other metrics.

The demo application's code in Python3 and NumPy is listed below:

The function survey_metrics(s1,s2) computes and the Hamming and Levenshtein distances, along with the corresponding values of similarity score for two input strings s1 and s2:

Python

def survey_metrics(s1,s2):
    # Compute all distance metrics for s1 and s2
    dists = { 'dl' : d_lev(s1,s2), 
              'hm' : hamming_dist(s1,s2) }
    # Compute the similarity score for each of the metrics
    score = { 'dl' : lev_score(s1,s2,dists['dl']), 
              'hm' : hamm_score(s1,s2,dists['hm']) } 
    # Return the statistics for all metrics, previously computed
    return np.array([{ 'name': name, 'd': dists[d], 's' : score[s] } \
        for [name,d,s] in zip(mt_names, dists.keys(), score.keys())], dtype=object)

Another survey(s1,s2) function generates the formatted output of distance and similarity score values computed for the s1 and s2 strings:

Python

def survey(s1,s2):
    # Compute the metrics and similarity scores for s1 and s2
    output = ""; results = survey_metrics(s1, s2)
    # Check if the Levenshtein metrics for s1 and s2 is valid
    valid = is_dl_valid(s1,s2,results[0]['d'],results[1]['d'])
    # Output strings s1 and s2 and their lengths
    output += "strings      : [ \"%s\" -> \"%s\" ]\n\n" % (s1, s2)
    # Output all metrics distance values for s1 and s2
    output += "distance     : [ " + " | ".join(["%s : %4.2f" % \
           (mt['name'],mt['d']) for mt in results]) + " ]\n"
    # Output all metrics similarity scores for s1 and s2
    output += "similarity   : [ " + " | ".join(["%s : %4.2f%%" % \
           (mt['name'],np.multiply(100, mt['s'])) for mt in results])
    # Output the Sorensen's score for s1 and s2
    output += " | Sorensen's Score: %4.2f%%" % sorensen_score(s1,s2) + " ]\n"
    # Output the verification status s1 and s2
    output += "verification : [ %s ]\n\n" % valid

    return output

Finally, the demo(filename) function loads the array of strings from the strings.txt file and performs the computations for each pair of the adjacent strings in the array, providing the distances and similarity scores outputs:

Python

def demo(filename):

    # Output the full path of the string file
    output = "Filename%s: %s\n\n" % \
        (" " * 5, os.path.abspath(filename));

    # Read all string from file 'strings.txt'
    with open(filename,'r') as f:
         strings = f.read().split('\n')
         # For each pair of strings compute the similarity score,
         # based on Levenshtein distance and other metrics
         for i in np.arange(len(strings)-1):
             if len(strings[i]) > 1 and len(strings[i + 1]) > 1:
                # Compute metrics of strings[i] and strings[i + 1], and output the survey
                print(survey(strings[i],strings[i + 1])); time.sleep(1)

    return output

mt_names = ["Levenshtein Distance", "Hamming Distance"]
app_logo = "Levenshtein Distance-Based Similarity Score 0.1a | " + \
           "Arthur V. Ratz @ CodeProject 2022"

if __name__ == "__main__":
    print(app_logo + "\n" + "=" * len(app_logo) + "\n\n")
    print(demo("strings.txt"))

Points of Interest

The Wagner-Fischer algorithm, discussed in this article, provides an ability to effectively evaluate the Levenshtein distance and similarity of textual data. This algorithm computes the distance of two strings, which is already the Damerau-Levenshtein distance, aware of the adjacent character transpositions. Finally, the Wagner-Fischer algorithm is easy to be implemented in most programming languages, not only in Haskell or Python but also C++, Java, Node.js, etc.

References

History

September 17^th , 2022 - the article was published.

License

This article, along with any associated source code and files, is licensed under The Code Project Open License (CPOL)

\(M[i-1][j] + 1\)	Deletion from S₁, Insertion to S₂
\(M[i][j-1] + 1\)	Insertion to S₁, Deletion from S₂
\(M[i-1][j-1] + 1_{(S_{1}[i]\neq{S_{2}[j]})}\)	Replacement of S₁[i] with S₂[j]

An Optimal Wagner-Fischer Algorithm For Approximate Strings Matching In Python And NumPy

Introduction

The Levenshtein Distance

An Optimal Wagner-Fischer Algorithm

S1 To S2 String Transformation

The Distance Values Stored In The Matrix M

Initialization

Levenshtein Distance of S1 and S2 Computation

Iterative Two Matrix Rows Algorithm

An Example...

The Levenshtein Distance To The Similarity Score Conversion

Using the code

Points of Interest

References

History

License

S₁ To S₂ String Transformation

Levenshtein Distance of S₁ and S₂ Computation