Fast and Stable Polynomial Root Finders - Part Two

Henrik Vestermark

4.60/5 (3 votes)

17 Oct 2023CPOL10 min read

5.3K

Fast and Stable Polynomial root finder for Polynomial with real coefficients

In Part 1, we elaborated how to find Polynomial roots and devised a modified Newton method dealing efficiently with Polynomials with complex coefficients. This part is all about finding Polynomial roots when the polynomial coefficients are real.

Introduction
The Easy Way Out
The Real or Complex Root Pitfall
What to Modify?
The Issue With Newton’s Method
A Suitable Starting Point for Root Finders
Evaluation of the Polynomial at a Complex Point
A Suitable Stopping Criterion for a Root
Error in Arithmetic Operations
- A Simple Upper bound
- A Better Upper Bound
Polynomial Deflation Strategy
The Implementation of K. Madsen Newton Algorithm
The C++ Code
Conclusion
References
History

Introduction

In the first paper (Part One), we developed a highly efficient and robust polynomial root-finder based on the Newton method, specifically designed for complex polynomial coefficients. Although many engineering problems involve polynomials with real coefficients, the core methodology remains applicable. Limiting the coefficients to real numbers does add some complexity to the implementation, but it also speeds up the calculations due to the reduced computational overhead associated with real arithmetic compared to complex arithmetic.

The Easy Way Out

Rather than storing polynomial coefficients in a std::vector<std::complex<double>>, we use a std::vector<double> now that the coefficients are real. A straightforward modification involves wrapping each coefficient reference with complex<double>(coefficients[i]). While this approach is functional, it overlooks the property that complex roots always appear in conjugate pairs, resulting in unnecessary conversions and reduced efficiency.

The Real or Complex Root Pitfall

From my perspective, implementing a root finder for real coefficients presents more challenges than one designed for complex coefficients. This is because each iteration may yield either one real root or a pair of complex roots. Complex roots always appear as conjugate pairs and extra caution is needed to avoid misclassifying a real root as two complex ones. If the algorithm veers into the complex plane but returns a value close to the real axis, a test is required to confirm the root's nature. Upon finding a root (designated as z), we check if P(z.real()) <= P(z). If true, we accept z.real() as the real root and deflate the polynomial accordingly. Otherwise, we recognize z and its complex conjugate as the roots, and proceed to deflate the polynomial using the quadratic formula, reducing its degree by two. Aside from this, the issue of multiple roots, addressed in the first paper, remains unchanged.

What to Modify?

Coefficients are now stored in a vector<double> as opposed to a vector<complex<double>>. It's important to note that complex roots still appear as conjugate pairs.

From Part One, the steps include:

Finding an initial start point
Executing the Newton iteration, including polynomial evaluation via the Horner method
Calculating the final upper bound for the errors in evaluation P(z)
Polynomial deflation
Solving the quadratic equation

Ad 1) The initial point-finding algorithm remains unchanged, requiring no code modifications.

Ad 2) Although the algorithm stays the same, optimizing the Horner method for real coefficients leads to fewer arithmetic operations. Code adjustments are needed for a more efficient implementation.

Ad 3) The real coefficients simplify the upper bound error calculation. We switch from the Grant-Hutchins algorithm to the Adam algorithm for increased efficiency.

Ad 4) Unlike with complex coefficients, where we find one root at a time, we now may find either a single real root or a pair of complex roots. Consequently, the polynomial can be divided by either a single real root or the quadratic form of the two complex roots.

Ad 5) The algorithm for solving the quadratic or linear polynomial differs, as it must account for whether the roots are real or complex. This wasn't an issue when dealing solely with complex roots.

Review each modified version:

Horner Method
Upper Bound Error Calculation
Real or Conjugate Complex Deflation
Linear or Quadratic Solutions

The Issue with Newton’s Method

In part one, we spent time detailing the issue with Newton’s method and also explained the multiple root issues. To overcome this, we need to multiply the Newton step by a factor m, leading to the modified Newton method.

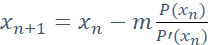
Where m is the multiplicity of the roots, this is all well-known stuff. The challenge is how to find m in real life.

A Suitable Starting Point for Root Finders

We use the same algorithm as in Part One, to find a suitable starting point and we just show the modified function for Polynomial with real coefficients.

This algorithm computes a reasonable and suitable starting point for our root search.

C++

// Compute the next starting point based on the polynomial coefficients
// A root will always be outside the circle from the origin and radius min
auto startpoint = [&](const vector<double>& a)
{
    const size_t n = a.size() - 1;
    double a0 = log(abs(a.back()));
    double min = exp((a0 - log(abs(a.front()))) / static_cast<double>(n));

    for (size_t i = 1; i < n; i++)
        if (a[i] != 0.0)
        {
            double tmp = exp((a0 - log(abs(a[i]))) / static_cast<double>(n - i));
            if (tmp < min)
                min = tmp;
        }

    return min * 0.5;
};

Evaluation of the Polynomial at a Complex Point

Most of the root-finding methods require us to evaluate a Polynomial at some point.

To evaluate a polynomial P(z) where P(z)=a_nzⁿ+a_n-1z^n-1,…,a₁z+a₀

We use the Horner [4] method given by the recurrence:

b_n=a_n
b_k=b_k-1z+a_k, k=n-1,…,0
P(z)=b₀

However, to avoid the complex arithmetic overhead, you can use an optimized method of Horner using real arithmetic.

In the case of a polynomial P(z) with real coefficients evaluated at a complex point z, we in general are using Horner recurrence but in a special version using only real arithmetic:

z=x+iy
p=-2x
q=x²+y²
b_n=a_n
b_n-1=a_n-1-pb_n
b_k=a_k-pb_k+1-qb_k+2, k=n-2,…,1
b₀=a₀-xb₁-qb₂
P(z)=b₀+iyb₁

The last term of this recurrence is then the value of P(z). Horner method has long been recognized as the most efficient way to evaluate a Polynomial at a given point. This algorithm works for real coefficients at a real or complex point.

C++

// Evaluate a polynomial with real coefficients a[] at a complex point z and
// return the result
// This is Horner's method of avoiding complex arithmetic
auto horner=[](const vector<double>& a, const complex<double> z)
{
    const size_t n = a.size() - 1;
    double p = -2.0 * z.real();
    double q = norm(z);
    double s = 0.0;
    double r = a[0];
    eval e;

    for (size_t i = 1; i < n; i++)
    {
        double t = a[i] - p * r - q * s;
        s = r;
        r = t;
    }

    e.z = z;
    e.pz = complex<double>(a[n] + z.real() * r - q * s, z.imag() * r);
    e.apz = abs(e.pz);
    return e;
};

A Suitable Stopping Criterion for a Root

In [8], they go over many different techniques to compute a suitable stopping criterion. See also [1]. Many root finders can use the method used by Adams [5] or Hitching [6] to find a suitable stopping criterion for polynomials with either real or complex coefficients.

When doing the iterative method, you will at some point need to consider what stopping criteria you want to apply for your root finders. Since most iterative root finders use the evaluation of the polynomial to progress it is only natural to continue our search until the evaluation of P(z) is close enough to 0 to accept the root at that point.

Error in Arithmetic Operations

J.H.Wilkinson in [7] has shown that the errors in performing algebraic operations are bound by:

ε<½β^1-t, β is the base, and t is the precision (assuming round to nearest)

Notice ½β^1-t= β^-t

For the Intel microprocessor series and the IEE754 standard for floating point operations β= 2 and t=53 for 64bit floating point arithmetic or 2-53

A Simple Upper Bound

A simple upper bound can then be found using the above information for a polynomial with degree n.

	Polynomials
*Number of operations:*	Real coefficient	Complex coefficients
Real point	\|a_o\|·2n·2^-53	\|a_o\|·4n·2^-53
Complex point	\|a_o\|·4n·2^-53	\|a_o\|·6n·2^-53

A Better Upper Bound

In this category, we have among others Adams [5] and Grant & Hitchins [6] stopping criteria for polynomials.

Polynomial root finders usually can handle polynomials with both real and complex coefficients evaluated at a real or complex number. Since Grant-Hitchin's stopping criterion is for Polynomials with complex coefficients, we will use Adams’ similar bound but for Polynomials with real coefficients.

Using the algorithm for Polynomial with real coefficients a_n evaluated at a complex point z, using Horner’s method as shown in the previous section.

Adams [5] has shown that an error bound can be computed using the following recurrence:

e_n=|b_n|7/9
e_k=e_k-1|z|+|b_k|, k=n-1,...,0
e=(4.5e₀-3.5(|b₀|+|b₁||z|)+|x||b₁|)½β^1-t

There exist other methods that are also useful to consider, see [1].

C++

// Calculate an upper bound for the rounding errors performed in a
// polynomial with real coefficient a[] at a complex point z.
// (Adam's test)
auto upperbound = [](const vector<double>& a, const complex<double> z)
{
    const size_t n = a.size() - 1;
    double p = -2.0 * z.real();
    double q = norm(z);
    double u = sqrt(q);
    double s = 0.0;
    double r = a[0];
    double e = fabs(r) * (3.5 / 4.5);
    double t;

    for (size_t i = 1; i < n; i++)
    {
        t = a[i] - p * r - q * s;
        s = r;
        r = t;
        e = u * e + fabs(t);
    }

    t = a[n] + z.real() * r - q * s;
    e = u * e + fabs(t);
    e = (4.5 * e - 3.5 * (fabs(t) + fabs(r) * u) +
        fabs(z.real())*fabs(r))*0.5*pow((double)_DBL_RADIX, -DBL_MANT_DIG + 1);

    return e;
};

Polynomial Deflation Strategy

After we have found a root, we need to make a synthetic division of that root up in the current Polynomial to reduce the polynomial degree and prepare to find the next root. The question then arises do you use Forward or Backward Deflation?
Wilkinson [7] has shown that to have a stable deflation process you should choose forward deflation if you find the roots of the polynomial in increasing magnitude and always deflate the polynomial with the lowest magnitude root first and of course, the opposite backward deflation when finding the roots with decreasing magnitude.

To do forward deflation, we try to solve the equations starting with the highest coefficients an:

a_nzⁿ+a_n-1z^n-1+⋯+a₁z+a₀=(b_n-1z^n-1+b_n-2z^n-2+⋯+b₁z+b₀)(z-R)

And R is the root.

Now solve it for b’s you get the recurrence:

b_n-1=a_n
b_k=a_k+1+R∙b_k+1, k=n-2,…,0

This simple algorithm works well for polynomials with real coefficients and real roots. A special case is real coefficients with complex roots. A complex root and its complex conjugated root will be the same as dividing by the polynomial P(Z) with 2^nd order polynomial of the two complex conjugated roots (x+iy) and (x-iy) or (z²-2xz+(x²+y²)). Letting r=-2x and u= x²+y²

You get:

P(z)=Q(z)(z²+rz+u)
where P(z)=a_nzⁿ+a_n-1z^n-1+⋯+a₁z+a₀
Q(z)=b_n-2z^n-2+b_n-3z^n-3+⋯+b₁z+b₀
The recurrence is then given by:
a_n=b_n-2
a_n-1=b_n-3+rb_n-2
a_k-2=b_k-2+rb_k-1+ub_k, k=n-2,...,3
a₂=b₀+rb₁+ub₂
a₁=rb₀+ub₁
a₀=ub₀

Now solve it for b’s you get:

b_n-2=a_n
b_n-3=a_n-1-rb_n-2
b_k=a_k+2-rb_k+1-ub_k, k=n-4,…,0

C++

// Real root forward deflation.
//
 auto realdeflation = [&](vector<double>& a, const double x)
 {
     const size_t n = a.size() - 1;
     double r=0.0;

     for (size_t i = 0; i < n; i++)
         a[i] = r = r * x + a[i];

     a.resize(n);    // Remove the highest degree coefficients.
 };

 // Complex root forward deflation for real coefficients
 //
 auto complexdeflation = [&](vector<double>& a, const complex<double> z)
 {
     const size_t n = a.size() - 1;
     double r = -2.0 * z.real();
     double u = norm(z);

     a[1] -= r * a[0];
     for (int i = 2; i < n - 1; i++)
         a[i] = a[i] - r * a[i - 1] - u * a[i - 2];

     a.resize(n - 1); // Remove top 2 highest degree coefficients
 };

The Implementation of K. Madsen Newton Algorithm

We follow the same implementation for the Newton method as in Part One and modify it only where needed to accommodate real arithmetic when appropriate and call the modified functions for finding the upper bound of error when using the Horner method to evaluate a polynomial at a complex point, polynomial deflation of a real or complex root.

The C++ Code

The C++ code below finds the Polynomial roots with Polynomial with real coefficients. The same version for Polynomial coefficients with complex coefficients can be found in part one. See [1] for details.

C++

/*
 *******************************************************************************
 *
 *                       Copyright (c) 2023
 *                       Henrik Vestermark
 *                       Denmark, USA
 *
 *                       All Rights Reserved
 *
 *   This source file is subject to the terms and conditions of
 *   Henrik Vestermark Software License Agreement which restricts the manner
 *   in which it may be used.
 *
 *******************************************************************************
*/
/*
 *******************************************************************************
 *
 * Module name     :   Newton.cpp
 * Module ID Nbr   :
 * Description     :   Solve n degree polynomial using Newton's (Madsen) method
 * --------------------------------------------------------------------------
 * Change Record   :
 *
 * Version      Author/Date     Description of changes
 * -------     -------------  ----------------------
 * 01.01        HVE/24Sep2023  Initial release
 *
 * End of Change Record
 * --------------------------------------------------------------------------
*/

// define version string
static char _VNEWTON_[] = "@(#)Newton.cpp 01.01 -- Copyright (C) Henrik Vestermark";

#include <algorithm>
#include <vector>
#include <complex>
#include <iostream>
#include <functional>

using namespace std;
constexpr int       MAX_ITER = 50;

// Find all polynomial zeros using a modified Newton method
// 1) Eliminate all simple roots (roots equal to zero)
// 2) Find a suitable starting point
// 3) Find a root using Newton
// 4) Divide the root up in the polynomial reducing its order with one
// 5) Repeat steps 2 to 4 until the polynomial is of the order of two 
//    whereafter the remaining one or two roots are found by the direct formula
// Notice:
//      The coefficients for p(x) is stored in descending order. coefficients[0] 
//      is a(n)x^n, coefficients[1] is a(n-1)x^(n-1),...,  
//      coefficients[n-1] is a(1)x, coefficients[n] is a(0)
//
static vector<complex<double>> PolynomialRoots(const vector<double>& coefficients)
{
    struct eval { complex<double> z{}; complex<double> pz{}; double apz{}; };
    const complex<double> complexzero(0.0);  // Complex zero (0+i0)
    size_t n;       // Size of Polynomial p(x) 
    eval pz;        // P(z)
    eval pzprev;    // P(zprev)
    eval p1z;       // P'(z)
    eval p1zprev;   // P'(zprev)
    complex<double> z;      // Use as temporary variable
    complex<double> dz;     // The current stepsize dz
    int itercnt;    // Hold the number of iterations per root
    vector<complex<double>> roots;  // Holds the roots of the Polynomial
    vector<double> coeff(coefficients.size()); // Holds the current coefficients of P(z)

    copy(coefficients.begin(), coefficients.end(), coeff.begin());
    // Step 1 eliminate all simple roots
    for (n = coeff.size() - 1; n > 0 && coeff.back() == 0.0; --n)
        roots.push_back(complexzero);  // Store zero as the root

    // Compute the next starting point based on the polynomial coefficients
    // A root will always be outside the circle from the origin and radius min
    auto startpoint = [&](const vector<double>& a)
    {
        const size_t n = a.size() - 1;
        double a0 = log(abs(a.back()));
        double min = exp((a0 - log(abs(a.front()))) / static_cast<double>(n));

        for (size_t i = 1; i < n; i++)
            if (a[i] != 0.0)
            {
                double tmp = exp((a0 - log(abs(a[i]))) / static_cast<double>(n - i));
                if (tmp < min)
                    min = tmp;
            }

        return min * 0.5;
    };

    // Evaluate a polynomial with real coefficients a[] at a complex point z and
    // return the result
    // This is Horner's method of avoiding complex arithmetic
    auto horner=[](const vector<double>& a, const complex<double> z)
    {
        const size_t n = a.size() - 1;
        double p = -2.0 * z.real();
        double q = norm(z);
        double s = 0.0;
        double r = a[0];
        eval e;

        for (size_t i = 1; i < n; i++)
        {
            double t = a[i] - p * r - q * s;
            s = r;
            r = t;
        }

        e.z = z;
        e.pz = complex<double>(a[n] + z.real() * r - q * s, z.imag() * r);
        e.apz = abs(e.pz);
        return e;
    };

    // Calculate a upper bound for the rounding errors performed in a
    // polynomial with real coefficient a[] at a complex point z.
    // (Adam's test)
    auto upperbound = [](const vector<double>& a, const complex<double> z)
    {
        const size_t n = a.size() - 1;
        double p = -2.0 * z.real();
        double q = norm(z);
        double u = sqrt(q);
        double s = 0.0;
        double r = a[0];
        double e = fabs(r) * (3.5 / 4.5);
        double t;

        for (size_t i = 1; i < n; i++)
        {
            t = a[i] - p * r - q * s;
            s = r;
            r = t;
            e = u * e + fabs(t);
        }

        t = a[n] + z.real() * r - q * s;
        e = u * e + fabs(t);
        e = (4.5 * e - 3.5 * (fabs(t) + fabs(r) * u) +
            fabs(z.real()) * fabs(r)) * 0.5 * pow((double)_DBL_RADIX, -DBL_MANT_DIG + 1);

        return e;
    };

    // Do Newton iteration for polynomial order higher than 2
    for (; n > 2; --n)
    {
        const double Max_stepsize = 5.0; // Allow the next step size to be 
                                         // up to 5 times larger than the previous step size
        const complex<double> rotation = complex<double>(0.6, 0.8);  // Rotation amount
        double r;               // Current radius
        double rprev;           // Previous radius
        double eps;             // The iteration termination value
        bool stage1 = true;     // By default it start the iteration in stage1
        int steps = 1;          // Multisteps if > 1
        vector<double> coeffprime;

        // Calculate coefficients of p'(x)
        for (int i = 0; i < n; i++)
            coeffprime.push_back(coeff[i] * double(n - i));

        // Step 2 find a suitable starting point z
        rprev = startpoint(coeff);      // Computed startpoint
        z = coeff[n - 1] == 0.0 ? complex<double>(1.0) : 
                                  complex<double>(-coeff[n] / coeff[n - 1]);
        z *= complex<double>(rprev) / abs(z);

        // Setup the iteration
        // Current P(z)
        pz = horner(coeff, z);

        // pzprev which is the previous z or P(0)
        pzprev.z = complex<double>(0);
        pzprev.pz = coeff[n];
        pzprev.apz = abs(pzprev.pz);

        // p1zprev P'(0) is the P'(0)
        p1zprev.z = pzprev.z;
        p1zprev.pz = coeff[n - 1];       // P'(0)
        p1zprev.apz = abs(p1zprev.pz);

        // Set previous dz and calculate the radius of operations.
        dz = pz.z;      // dz=z-zprev=z since zprev==0
        r = rprev *= Max_stepsize; // Make a reasonable radius of the 
                                   // maximum step size allowed
        // Preliminary eps computed at point P(0) by a crude estimation
        eps = 2 * n * pzprev.apz * pow((double)_DBL_RADIX, -DBL_MANT_DIG);

        // Start iteration and stop if z doesnt change or apz <= eps
        // we do z+dz!=z instead of dz!=0. if dz does not change z 
        // then we accept z as a root
        for (itercnt = 0; pz.z + dz != pz.z && 
             pz.apz > eps && itercnt < MAX_ITER; itercnt++)
        {
            // Calculate current P'(z)
            p1z = horner(coeffprime, pz.z);
            if (p1z.apz == 0.0)                 // P'(z)==0 then rotate and try again
                dz *= rotation * complex<double>(Max_stepsize);  // Multiply with 5 
                                                      // to get away from saddlepoint
            else
            {
                dz = pz.pz / p1z.pz;  // next dz
                // Check the Magnitude of Newton's step
                r = abs(dz);
                if (r > rprev) // Large than 5 times the previous step size
                {   // then rotate and adjust step size to prevent 
                    // wild step size near P'(z) close to zero
                    dz *= rotation * complex<double>(rprev/r);
                    r = abs(dz);
                }

                rprev = r * Max_stepsize;  // Save 5 times the current step size 
                                           // for the next iteration check 
                                           // of reasonable step size
                // Calculate if stage1 is true or false. Stage1 is false 
                // if the Newton converge otherwise true
                z = (p1zprev.pz - p1z.pz) / (pzprev.z - pz.z);
                stage1 = (abs(z) / p1z.apz > p1z.apz / pz.apz / 4) || (steps != 1);
            }

            // Step accepted. Save pz in pzprev
            pzprev = pz;
            z = pzprev.z - dz;      // Next z
            pz = horner(coeff, z); //ff = pz.apz;
            steps = 1;
            if (stage1)
            {  // Try multiple steps or shorten steps depending if P(z) 
               // is an improvement or not P(z)<P(zprev)
                bool div2;
                complex<double> zn;
                eval npz;

                zn = pz.z;
                for (div2 = pz.apz > pzprev.apz; steps <= n; ++steps)
                {
                    if (div2 == true)
                    {  // Shorten steps
                        dz *= complex<double>(0.5);
                        zn = pzprev.z - dz;
                    }
                    else
                        zn -= dz;  // try another step in the same direction

                    // Evaluate new try step
                    npz = horner(coeff, zn);
                    if (npz.apz >= pz.apz)
                        break; // Break if no improvement

                    // Improved => accept step and try another round of step
                    pz = npz;

                    if (div2 == true && steps == 2)
                    {   // To many shorten steps => try another direction and break
                        dz *= rotation;
                        z = pzprev.z - dz;
                        pz = horner(coeff, z);
                        break;
                    }
                }
            }
            else
            {   // calculate the upper bound of error using Grant & Hitchins's 
                // test for complex coefficients
                // Now that we are within the convergence circle.
                eps = upperbound(coeff, pz.z);
            }
        }

        // Real root forward deflation.
        //
        auto realdeflation = [&](vector<double>& a, const double x)
        {
            const size_t n = a.size() - 1;
            double r=0.0;

            for (size_t i = 0; i < n; i++)
                a[i] = r = r * x + a[i];

            a.resize(n);    // Remove the highest degree coefficients.
        };

        // Complex root forward deflation for real coefficients
        //
        auto complexdeflation = [&](vector<double>& a, const complex<double> z)
        {
            const size_t n = a.size() - 1;
            double r = -2.0 * z.real();
            double u = norm(z);

            a[1] -= r * a[0];
            for (int i = 2; i < n - 1; i++)
                a[i] = a[i] - r * a[i - 1] - u * a[i - 2];

            a.resize(n - 1); // Remove top 2 highest degree coefficienst
        };


        // Check if there is a very small residue in the imaginary part by trying
        // to evaluate P(z.real). if that is less than P(z). 
        // We take that z.real() is a better root than z.
        z = complex<double>(pz.z.real(), 0.0);
        pzprev = horner(coeff, z);
        if (pzprev.apz <= pz.apz)
        { // real root
            pz = pzprev;
            // Save the root
            roots.push_back(pz.z);
            realdeflation(coeff, pz.z.real());
        }
        else
        {   // Complex root
            // Save the root
            roots.push_back(pz.z);
            roots.push_back(conj(pz.z));
            complexdeflation(coeff, pz.z);
            --n;
        }
     
    }   // End Iteration

    // Solve any remaining linear or quadratic polynomial
    // For Polynomial with real coefficients a[],
    // The complex solutions are stored in the back of the roots
    auto quadratic = [&](const std::vector<double>& a)
    {
        const size_t n = a.size() - 1;
        complex<double> v;
        double r;

        // Notice that a[0] is !=0 since roots=zero has already been handle
        if (n == 1)
            roots.push_back(complex<double>(-a[1] / a[0],0));
        else
        {
            if (a[1] == 0.0)
            {
                r = -a[2] / a[0];
                if (r < 0)
                {
                    r = sqrt(-r);
                    v = complex<double>(0, r);
                    roots.push_back(v);
                    roots.push_back(conj(v));
                }
                else
                {
                    r = sqrt(r);
                    roots.push_back(complex<double>(r));
                    roots.push_back(complex<double>(-r));
                }
            }
            else
            {
                r = 1.0 - 4.0 * a[0] * a[2] / (a[1] * a[1]);
                if (r < 0)
                {
                    v = complex<double>(-a[1] / (2.0 * a[0]), a[1] * 
                                        sqrt(-r) / (2.0 * a[0]));
                    roots.push_back(v);
                    roots.push_back(conj(v));
                }
                else
                {
                    v = complex<double>((-1.0 - sqrt(r)) * a[1] / (2.0 * a[0]));
                    roots.push_back(v);
                    v = complex<double>(a[2] / (a[0] * v.real()));
                    roots.push_back(v);
                }
            }
        }
        return;
    };


    if (n > 0)
        quadratic(coeff);

    return roots;
}

Example 1

Here is an example of how the above source code is working. Notice the statistics detailing the amount spent in stage 1 and stage 2 and how many rotations were needed.

For the real Polynomial:

+1x^4-10x^3+35x^2-50x+24
Start Newton Iteration for Polynomial=+1x^4-10x^3+35x^2-50x+24
              Stage 1=>Stop Condition. |f(z)|<2.13e-14
              Start    : z[1]=0.2 dz=2.40e-1 |f(z)|=1.4e+1
Iteration: 1
              Newton Step:  z[1]=0.6 dz=-3.98e-1 |f(z)|=3.9e+0
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=1 dz=-3.98e-1 |f(z)|=2.0e-1
                      : Improved=>Continue stepping
              Try Step:  z[1]=1 dz=-3.98e-1 |f(z)|=9.9e-1
                      : No improvement=>Discard last try step
Iteration: 2
              Newton Step:  z[1]=1 dz=3.87e-2 |f(z)|=1.6e-2
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=1 dz=3.87e-2 |f(z)|=2.7e-1
                      : No improvement=>Discard last try step
Iteration: 3
              Newton Step:  z[1]=1 dz=-2.62e-3 |f(z)|=7.6e-5
              In Stage 2=>New Stop Condition: |f(z)|<2.18e-14
Iteration: 4
              Newton Step:  z[1]=1 dz=-1.26e-5 |f(z)|=1.8e-9
              In Stage 2=>New Stop Condition: |f(z)|<2.18e-14
Iteration: 5
              Newton Step:  z[1]=1 dz=-2.93e-10 |f(z)|=3.6e-15
              In Stage 2=>New Stop Condition: |f(z)|<2.18e-14
Stop Criteria satisfied after 5 Iterations
Final Newton  z[1]=1 dz=-2.93e-10 |f(z)|=3.6e-15
Alteration=0% Stage 1=40% Stage 2=60%
              Deflate the real root z=1.0000000000000007
Start Newton Iteration for Polynomial=+1x^3-9x^2+25.999999999999993x-23.99999999999999
              Stage 1=>Stop Condition. |f(z)|<1.60e-14
              Start    : z[1]=0.5 dz=4.62e-1 |f(z)|=1.4e+1
Iteration: 1
              Newton Step:  z[1]=1 dz=-7.54e-1 |f(z)|=3.9e+0
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=2 dz=-7.54e-1 |f(z)|=6.4e-2
                      : Improved=>Continue stepping
              Try Step:  z[1]=3 dz=-7.54e-1 |f(z)|=2.6e-1
                      : No improvement=>Discard last try step
Iteration: 2
              Newton Step:  z[1]=2 dz=-2.95e-2 |f(z)|=2.7e-3
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=2 dz=-2.95e-2 |f(z)|=5.4e-2
                      : No improvement=>Discard last try step
Iteration: 3
              Newton Step:  z[1]=2 dz=-1.32e-3 |f(z)|=5.3e-6
              In Stage 2=>New Stop Condition: |f(z)|<1.42e-14
Iteration: 4
              Newton Step:  z[1]=2 dz=-2.63e-6 |f(z)|=2.1e-11
              In Stage 2=>New Stop Condition: |f(z)|<1.42e-14
Iteration: 5
              Newton Step:  z[1]=2 dz=-1.04e-11 |f(z)|=3.6e-15
              In Stage 2=>New Stop Condition: |f(z)|<1.42e-14
Stop Criteria satisfied after 5 Iterations
Final Newton  z[1]=2 dz=-1.04e-11 |f(z)|=3.6e-15
Alteration=0% Stage 1=40% Stage 2=60%
              Deflate the real root z=2.0000000000000036
Solve Polynomial=+1x^2-6.9999999999999964x+11.999999999999975 directly
Using the Newton Method, the Solutions are:
X1=1.0000000000000007
X2=2.0000000000000036
X3=4.000000000000011
X4=2.999999999999986

Example 2

The same example just with a double root at x=1. We see that each step is a double step in line with a multiplicity of 2 for the first root. Notice that for a multiple root it spend all the search in stage1 and 0% in stage 2.

For the real Polynomial:
+1x^4-9x^3+27x^2-31x+12
Start Newton Iteration for Polynomial=+1x^4-9x^3+27x^2-31x+12
              Stage 1=>Stop Condition. |f(z)|<1.07e-14
              Start    : z[1]=0.2 dz=1.94e-1 |f(z)|=6.9e+0
Iteration: 1
              Newton Step:  z[1]=0.5 dz=-3.23e-1 |f(z)|=2.0e+0
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=0.8 dz=-3.23e-1 |f(z)|=1.8e-1
                      : Improved=>Continue stepping
              Try Step:  z[1]=1 dz=-3.23e-1 |f(z)|=1.4e-1
                      : Improved=>Continue stepping
              Try Step:  z[1]=1 dz=-3.23e-1 |f(z)|=8.9e-1
                      : No improvement=>Discard last try step
Iteration: 2
              Newton Step:  z[1]=1 dz=8.71e-2 |f(z)|=3.1e-2
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=1 dz=8.71e-2 |f(z)|=9.6e-4
                      : Improved=>Continue stepping
              Try Step:  z[1]=0.9 dz=8.71e-2 |f(z)|=6.5e-2
                      : No improvement=>Discard last try step
Iteration: 3
              Newton Step:  z[1]=1 dz=-6.27e-3 |f(z)|=2.4e-4
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=1 dz=-6.27e-3 |f(z)|=2.6e-8
                      : Improved=>Continue stepping
              Try Step:  z[1]=1 dz=-6.27e-3 |f(z)|=2.3e-4
                      : No improvement=>Discard last try step
Iteration: 4
              Newton Step:  z[1]=1 dz=-3.28e-5 |f(z)|=6.5e-9
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=1 dz=-3.28e-5 |f(z)|=0
                      : Improved=>Continue stepping
              Try Step:  z[1]=1 dz=-3.28e-5 |f(z)|=6.5e-9
                      : No improvement=>Discard last try step
Stop Criteria satisfied after 4 Iterations
Final Newton  z[1]=1 dz=-3.28e-5 |f(z)|=0
Alteration=0% Stage 1=100% Stage 2=0%
              Deflate the real root z=0.9999999982094424
Start Newton Iteration for Polynomial=+1x^3-8.000000001790557x^2+19.000000012533903x-12.000000021486692
              Stage 1=>Stop Condition. |f(z)|<7.99e-15
              Start    : z[1]=0.3 dz=3.16e-1 |f(z)|=6.8e+0
Iteration: 1
              Newton Step:  z[1]=0.8 dz=-4.75e-1 |f(z)|=1.5e+0
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=1 dz=-4.75e-1 |f(z)|=1.3e+0
                      : Improved=>Continue stepping
              Try Step:  z[1]=2 dz=-4.75e-1 |f(z)|=2.1e+0
                      : No improvement=>Discard last try step
Iteration: 2
              Newton Step:  z[1]=0.9 dz=3.54e-1 |f(z)|=5.7e-1
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=0.6 dz=3.54e-1 |f(z)|=3.7e+0
                      : No improvement=>Discard last try step
Iteration: 3
              Newton Step:  z[1]=1 dz=-8.28e-2 |f(z)|=3.6e-2
              In Stage 2=>New Stop Condition: |f(z)|<6.64e-15
Iteration: 4
              Newton Step:  z[1]=1 dz=-5.87e-3 |f(z)|=1.7e-4
              In Stage 2=>New Stop Condition: |f(z)|<6.66e-15
Iteration: 5
              Newton Step:  z[1]=1 dz=-2.88e-5 |f(z)|=4.1e-9
              In Stage 2=>New Stop Condition: |f(z)|<6.66e-15
Iteration: 6
              Newton Step:  z[1]=1 dz=-6.90e-10 |f(z)|=8.9e-16
              In Stage 2=>New Stop Condition: |f(z)|<6.66e-15
Stop Criteria satisfied after 6 Iterations
Final Newton  z[1]=1 dz=-6.90e-10 |f(z)|=8.9e-16
Alteration=0% Stage 1=33% Stage 2=67%
              Deflate the real root z=1.0000000017905577
Solve Polynomial=+1x^2-6.999999999999999x+12 directly
Using the Newton Method, the Solutions are:
X1=0.9999999982094424
X2=1.0000000017905577
X3=3.999999999999995
X4=3.0000000000000036

Example 3

A test polynomial with both real and complex conjugated roots.

For the real Polynomial:
+1x^4-8x^3-17x^2-26x-40
Start Newton Iteration for Polynomial=+1x^4-8x^3-17x^2-26x-40
              Stage 1=>Stop Condition. |f(z)|<3.55e-14
              Start    : z[1]=-0.8 dz=-7.67e-1 |f(z)|=2.6e+1
Iteration: 1
              Newton Step:  z[1]=-2 dz=1.65e+0 |f(z)|=7.0e+1
              Function value increase=>try shorten the step
              Try Step:  z[1]=-2 dz=8.24e-1 |f(z)|=3.1e+0
                      : Improved=>Continue stepping
              Try Step:  z[1]=-1 dz=4.12e-1 |f(z)|=1.8e+1
                      : No improvement=>Discard last try step
Iteration: 2
              Newton Step:  z[1]=-2 dz=6.27e-2 |f(z)|=1.5e-1
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=-2 dz=6.27e-2 |f(z)|=3.7e+0
                      : No improvement=>Discard last try step
Iteration: 3
              Newton Step:  z[1]=-2 dz=-2.74e-3 |f(z)|=2.9e-4
              In Stage 2=>New Stop Condition: |f(z)|<1.91e-14
Iteration: 4
              Newton Step:  z[1]=-2 dz=-5.51e-6 |f(z)|=1.2e-9
              In Stage 2=>New Stop Condition: |f(z)|<1.91e-14
Iteration: 5
              Newton Step:  z[1]=-2 dz=-2.22e-11 |f(z)|=0
              In Stage 2=>New Stop Condition: |f(z)|<1.91e-14
Stop Criteria satisfied after 5 Iterations
Final Newton  z[1]=-2 dz=-2.22e-11 |f(z)|=0
Alteration=0% Stage 1=40% Stage 2=60%
              Deflate the real root z=-1.650629191439388
Start Newton Iteration for Polynomial=+1x^3-9.650629191439387x^2-1.0703897408530487x-24.233183447530717
              Stage 1=>Stop Condition. |f(z)|<1.61e-14
              Start    : z[1]=-0.8 dz=-7.92e-1 |f(z)|=3.0e+1
Iteration: 1
              Newton Step:  z[1]=1 dz=-1.86e+0 |f(z)|=3.5e+1
              Function value increase=>try shorten the step
              Try Step:  z[1]=0.1 dz=-9.30e-1 |f(z)|=2.5e+1
                      : Improved=>Continue stepping
              Try Step:  z[1]=-0.3 dz=-4.65e-1 |f(z)|=2.5e+1
                      : No improvement=>Discard last try step
Iteration: 2
              Newton Step:  z[1]=-7 dz=6.71e+0 |f(z)|=7.2e+2
              Function value increase=>try shorten the step
              Try Step:  z[1]=-3 dz=3.35e+0 |f(z)|=1.5e+2
                      : Improved=>Continue stepping
              Try Step:  z[1]=-2 dz=1.68e+0 |f(z)|=4.9e+1
                      : Improved=>Continue stepping
                      : Probably local saddlepoint=>Alter Direction:  
                            z[1]=(-0.4-i0.7) dz=(5.03e-1+i6.71e-1) |f(z)|=2.1e+1
Iteration: 3
              Newton Step:  z[1]=(0.3-i2) dz=(-6.86e-1+i1.17e+0) |f(z)|=1.9e+1
              Function value decrease=>try multiple steps in that direction
              Try Step:  z[1]=(1-i3) dz=(-6.86e-1+i1.17e+0) |f(z)|=8.4e+1
                      : No improvement=>Discard last try step
Iteration: 4
              Newton Step:  z[1]=(-0.09-i1) dz=(4.11e-1-i3.44e-1) |f(z)|=3.0e+0
              In Stage 2=>New Stop Condition: |f(z)|<1.29e-14
Iteration: 5
              Newton Step:  z[2]=(-0.18-i1.5) dz=(8.71e-2+i4.72e-2) |f(z)|=1.1e-1
              In Stage 2=>New Stop Condition: |f(z)|<1.36e-14
Iteration: 6
              Newton Step:  z[3]=(-0.175-i1.55) dz=(-3.24e-3+i1.00e-3) |f(z)|=1.3e-4
              In Stage 2=>New Stop Condition: |f(z)|<1.36e-14
Iteration: 7
              Newton Step:  z[6]=(-0.174685-i1.54687) dz=(1.28e-6+i3.82e-6) |f(z)|=1.8e-10
              In Stage 2=>New Stop Condition: |f(z)|<1.36e-14
Iteration: 8
              Newton Step:  z[12]=(-0.174685404280-i1.54686888723) dz=(-2.07e-12-i5.33e-12) |f(z)|=3.6e-15
              In Stage 2=>New Stop Condition: |f(z)|<1.36e-14
Stop Criteria satisfied after 8 Iterations
Final Newton  z[12]=(-0.174685404280-i1.54686888723) dz=(-2.07e-12-i5.33e-12) |f(z)|=3.6e-15
Alteration=13% Stage 1=38% Stage 2=63%
              Deflate the complex conjugated root z=(-0.17468540428030604-i1.5468688872313963)
Solve Polynomial=+1x-10 directly
Using the Newton Method, the Solutions are:
X1=-1.650629191439388
X2=(-0.17468540428030604-i1.5468688872313963)
X3=(-0.17468540428030604+i1.5468688872313963)
X4=10

Conclusion

We have presented a refined Newton method, building upon the framework established in Part One, to efficiently and stably find roots of polynomials with real coefficients. While Part One focused on polynomials with complex coefficients—where roots could still be real—this second part delves into polynomials with real coefficients. Part Three will explore adjustments needed for higher-order methods, such as Halley's method, while Part Four will demonstrate the ease of integrating alternative methods like Laguerre's into the existing framework. A web-based polynomial solver showcasing these various methods is available for further exploration and can be found on http://www.hvks.com/Numerical/websolver.php. Polynomial roots finder that demonstrate many of these methods in action.

References

H. Vestermark. A practical implementation of Polynomial root finders. Practical implementation of Polynomial root finders. www.hvks.com/Numerical/papers.html
Madsen. A root-finding algorithm based on Newton Method, Bit 13 (1973) 71-75.
A. Ostrowski, Solution of equations and systems of equations, Academic Press, 1966.
Wikipedia Horner’s Method: https://en.wikipedia.org/wiki/Horner%27s_method
Adams, D A stopping criterion for polynomial root finding.
Communication of the ACM Volume 10/Number 10/ October 1967 Page 655-658
Grant, J. A. & Hitchins, G D. Two algorithms for the solution of polynomial equations to limiting machine precision. The Computer Journal Volume 18 Number 3, pages 258-264
Wilkinson, J H, Rounding errors in Algebraic Processes, Prentice-Hall Inc, Englewood Cliffs, NJ 1963
McNamee, J.M., Numerical Methods for Roots of Polynomials, Part I & II, Elsevier, Kidlington, Oxford 2009
H. Vestermark, “A Modified Newton and higher orders Iteration for multiple roots.”, www.hvks.com/Numerical/papers.html
M.A. Jenkins & J.F. Traub, ”A three-stage Algorithm for Real Polynomials using Quadratic iteration”, SIAM J Numerical Analysis, Vol. 7, No.4, December 1970.

History

15^th October, 2023: Initial release of Part 2

License

This article, along with any associated source code and files, is licensed under The Code Project Open License (CPOL)