Through sample executions, the article demonstrates that Smoothsort outperforms Heapsort particularly when the original array is nearly or completely sorted, emphasizing Smoothsort's efficiency in such scenarios.
1. Introduction
In 1981, the late Professor Edsger Wybe Dijkstra wrote an article on a sorting algorithm that he named Smoothsort as an alternative to Heapsort for sorting in situ (i.e., in place) a one dimensional array of unspecified data type (Dijkstra 1981). Heapsort is one of the fastest sorting algorithms: for an array of size N, its guaranteed execution time is O( N log2 N ). However, a disadvantage is that its execution time is the same even if the original array is nearly (or completely) sorted. In contrast, Smoothsort executes in time O( N log2 N ) on an arbitrary array, but transitions smoothly to O( N ) if the array is nearly sorted.
2. Binary Trees and Heaps
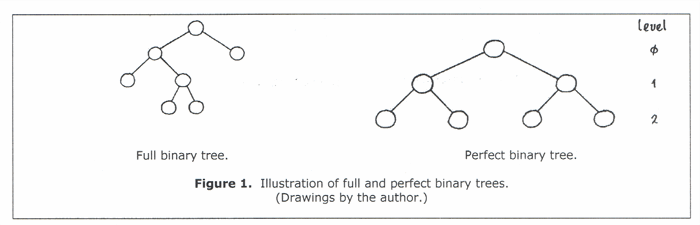
In a binary tree, each parent node has at most two children. A node with at least one child is a parent node, while nodes with no children are leaves. A full binary tree is one in which no node has only one child, and the nodes of the tree satisfy the property # of leaves = # internal nodes + 1.
A perfect binary tree is a full tree in which all the leaves are at the same level. A binary tree is complete if the next-to-last level is full of nodes and the leaves at the last level are justified to the left. These trees are illustrated in Figures 1 and 2.

If h is the height (number of levels) of a perfect binary tree, then it has (2 ^ (h + 1)) - 1 total nodes, of which 2 ^ h are leaves and (2 ^ h) - 1 are internal nodes.
In an implementation of binary trees by means of one-dimensional arrays, the elements of the array correspond to the nodes of the tree, and indices into the array correspond to the edges linking a node to its children (if any). Given the index into a node there must be an efficient way to determine the indices of its children. In order to store an N-node binary tree in an N-element array, the tree can be traversed level-by-level, top-to-bottom, and left-to-right, storing the nodes in consecutive array elements. Such is the well-known order of breadth-first search.
A heap is a binary tree that satisfies two properties. In terms of its shape, a heap is a complete binary tree. In terms of the ordering of the elements stored, a heap is a max-heap if the value stored in every parent node is greater than or equal to the value stored in each of its children. On the other hand, in a min-heap the value stored in a parent node is less than or equal to the values in its children. Leaf nodes vaccuously satisfy the order property of heaps. Examples of max- and min-heaps containing prime numbers are shown in Figure 3.

For a 0-based, N-element array x, given the index i into node x[ i ] satisfying the constraints 0 <= i <= (N - 3)/2, the left and right children of such a node are, respectively, x[ i * 2 + 1 ] and x[ i * 2 + 2 ].
3. Heapsort
J.W.J. Williams (1964) published his Algol implementation of Heapsort for 1-based arrays. This section describes the logic underlying Heapsort and the author’s generic implementation of this algorithm in C#. As a prelude to Smoothsort, the formal specification of the pre-condition before, and post-condition after the execution of Heapsort was given by van Gasteren, Dijkstra and Feijen (1981), as shown in Dijkstra’s handwriting in Figure 4.

In words, the pre-condition states that for a 0-based, N-element array m of integers, the array contains an arbitrary collection (i.e., a bag) of integers and, after the execution of Heapsort, the post-condition states that for all indices i and j satisfying the conditions 0 <= i < j and 1 <= j < N the elements of m are in sorted order. Of course, the specification is valid for any type of array elements. An implementation of Heapsort for integer-element arrays is described next.
The logic of Heapsort is simple. Assuming that an array is to be sorted in ascending order, rearrange the elements to create a max-heap, put the maximum element in its proper place, restore the max-heap property from the first to the next-to-last element, and repeat the process until there are no more elements to process. The result of the sort is a min-heap. This verbal description is implemented as follows. The C# code is adapted from C++ code written by the author (Orejel 2003), and it is assumed to reside within a static class in a console application.
static void HeapSort( int[] m )
{
int N = m.Length;
BuildHeap( m, N >> 1, N - 1 );
SortNodes( m, N - 1 );
}
As noted in the remarks section of function HeapSort, the process of building a max-heap starts at the midpoint of the array. Once the heap has been built, the nodes can be sorted.

Figure 5a shows a tail-recursive implementation of function BuildHeap. The function is tail-recursive because nothing must be done after the recursive call returns. Consequently, Figure 5b shows an iterative version in which the tail-recursive call has been replaced by its equivalent code. Assuming the existence of the proper functionality to display arrays and trees (to be dealt with later), Figure 6 shows a sample array and the tree structure that results after the execution of BuildHeap.

Function ReheapDown is the workhorse of BuildHeap. As long as there are nodes (i.e., array elements) to be examined, if a parent node is greater than the maximum of its children, the nodes are interchanged and the process continues with the maximum child as the new parent. The function is also tail-recursive, and the comments in it indicate how to make the function iterative: uncomment the label, comment out the recursive call, and uncomment the code that replaces the call.
static void ReheapDown( int[] m, int parent, int bottom )
{
int maxChild, leftChild;
leftChild = ( parent << 1 ) + 1;
if ( leftChild <= bottom )
{
maxChild = MaxChildIndex( m, leftChild, bottom );
if ( m[ parent ] < m[ maxChild ] )
{
Swap( ref m[ parent ], ref m[ maxChild ] );
ReheapDown( m, maxChild, bottom );
}
}
}
The two auxiliary functions called by ReheapDown are MaxChildIndex which determines the index of the maximum child and, of course, Swap to perform the interchange of array elements. Observe that it is essential to pass to Swap its arguments by reference.
static int MaxChildIndex( int[] m, int leftChild, int bottom )
{
int rightChild = leftChild + 1;
return ( leftChild == bottom )
? leftChild
: ( m[ leftChild ] > m[ rightChild ] )
? leftChild
: rightChild;
}
static void Swap( ref int x, ref int y )
{
int t = x; x = y; y = t;
}
The last function to be written is SortNodes. It puts the maximum heap element in its place at the end of the array, calls ReheapDown to restore the max-heap property from the first to the next-to-last element, and finally calls itself recursively. As might have been anticipated, SortNodes is also tail-recursive and the comments in the code indicate how to make it iterative.
static void SortNodes( int[] m, int bottom )
{
if ( bottom > 0 )
{
Swap( ref m[ 0 ], ref m[ bottom-- ] );
ReheapDown( m, 0, bottom );
SortNodes( m, bottom );
}
}
Figure 7 shows the min-heap tree structure and the array at the end of the execution of SortNodes. As a final note, if HeapSort is called with the same array after sorting, it will perform the same actions as if the array had not been sorted. This concludes the description of Heapsort over an array of integer values.

4. Generic Heapsort
This section is not a re-hash of the code in Section 3. First and foremost, the code is generic in that it can handle array elements of an arbitrary data type that satisfies a very simple constraint. Secondly, it uses some library functions (to be described as they are used) that are naturally common to sorting algorithms. And thirdly, the code is iterative without the use of labels and goto statements. So, this section is a prelude to things to come, namely GenericSmoothSort.
In order to handle arbitrary data types, the functions that implement Heapsort must have a generic type parameter <T>, and such a type must be constrained by the IComparable interface. The class name and the function signatures in the GenericHeapSort namespace are shown in Figure 8. The function names in Section 3 have been retained. There is a using statement indicating that the code has a reference to a library named UtilSortLib, which implements functions that are common to sorting algorithms. In particular, observe that the HS class does not include a Swap function because it is a fundamental operation in any sorting algorithm, and thus it belongs in that library.
The library UtilSortLib has three classes, one for static variables and two for functions: TypedUfn<T> (short for "Typed Utility function") and UntypedUfn (short for "Un-typed Utility function"). Most of the functions have to do with displaying results on the console and are described in Section 7, but some will be described as they are used.

The specification of a type parameter after the name of each of the functions allows them to take a generic array as a parameter, and the where constraint indicates that the parameter must be subject to comparison. This means that there must be a CompareTo function for the data type of the array elements. According to the Microsoft documentation, there is such a function for all the types that can be ordered or sorted, which is the case for all C# primitive data types. However, as will be illustrated later, an arbitrary data type must explicitly implement the comparison function.
With the exception of displaying on the console two utility global variables (the count of swap operations and the count of comparisons), and the array in tree form (by calling TypedUfn<T>.DisplayTree), function HeapSort<T> is the generic version of its counterpart in Section 3.
public static void HeapSort<T>( T[] arr ) where T : IComparable<T>
{
int n = arr.Length - 1;
BuildHeap( arr, n >> 1, n );
Console.Write( "After {BuildHeap}: " );
Console.WriteLine( "{0} swaps; {1} comparisons", Uvar.swapCount, Uvar.compCount );
TypedUfn<T>.DisplayTree( "after {BuildHeap}", arr );
SortNodes( arr, n );
}
Functions BuildHeap<T> and ReheapDown<T> are both iterative, and do not use a target label and corresponding goto statement. However, observe the use of a break statement in function ReheapDown. Without it, the while loop in the function would not terminate. This illustrates the fact that it is not trivial to eliminate labels and goto statements that implement loops.
private static void ReheapDown<T>( T[] arr, int parent, int bottom )
where T : IComparable<T>
{
int maxChild, leftChild;
leftChild = ( parent << 1 ) + 1;
while ( leftChild <= bottom )
{
maxChild = MaxChildIndex( arr, leftChild, bottom );
int cmp = arr[ parent ].CompareTo( arr[ maxChild ] );
if ( UntypedUfn.IsLT( cmp ) )
{
TypedUfn<T>.Swap( "ReheapDown", arr, parent, maxChild );
parent = maxChild;
leftChild = ( parent << 1 ) + 1;
}
else
{
break;
}
}
}
Function ReheapDown<T> calls a CompareTo function on instances of a generic data type. By definition in the Microsoft documentation, if x and y are instances of the same data type, the call x.CompareTo( y ) returns an integer value which is less than 0 if x is less than y, 0 if x is equal to y, or greater than 0 if x is greater than y. The untyped utility function UntypedUfn.IsLT returns true if its argument is less than 0 (the assertion in the comment for the else part, states that function UntypedUfn.IsGE would return true given the same argument).
public static bool IsLT( int cmp )
{
++Uvar.cmpCount;
return cmp < 0;
}
There are additional untyped comparison functions (IsLE, IsEQ, IsGT) with the obvious meanings. All of them increment the global count of comparisons performed.
In the if clause, ReheapDown calls one of the two versions of the typed utility function TypedUfn<T>.Swap, which inspects the value of a global variable set from an enumeration to control the output to the console.
public enum OutMode { quiet, verbose }
public static void Swap( string fName, T[] m, int i, int j )
{
++Uvar.swapCount;
if ( Uvar.OutMode == OutMode.verbose )
{
TypedUfn<T>.DisplayArray( "", m );
DisplaySwap( fName, i, m[ i ], j, m[ j ] );
}
Swap( ref m[ i ], ref m[ j ] );
}
Observe that function Swap does not have a type parameter because it resides inside a typed class. This function increments the global count of swap operations and, when Uvar.outMode equals OutMode.verbose, it calls the typed function DisplayArray and the untyped function DisplaySwap. Finally, the actual swap is performed by the two-parameter function Swap.
public static void Swap( ref T x, ref T y )
{
T tmp = x;
x = y; y = tmp;
}
Function MaxChildIndex<T> has the same logic as in Section 3, but it calls the CompareTo function and the utility function UntypedUfn.IsGT. Function SortNodes<T> is the generic iterative version of its tail-recursive counterpart.
private static int MaxChildIndex<T>( T[] arr, int leftChild, int bottom )
where T : IComparable<T>
{
int rightChild = leftChild + 1;
return ( leftChild == bottom )
? leftChild
: UntypedUfn.IsGT( arr[ leftChild ].CompareTo( arr[ rightChild ] ) )
? leftChild
: rightChild;
}
private static void SortNodes<T>( T[] arr, int bottom ) where T : IComparable<T>
{
while ( bottom > 0 )
{
TypedUfn<T>.Swap( " SortNodes", arr, 0, bottom-- );
ReheapDown( arr, 0, bottom );
}
}
For comparison purposes, the execution of generic HeapSort will be illustrated hand-in-hand with the execution of generic SmoothSort. But, for the curious reader, Figure 9 shows the result of HeapSort on an array of the first 25 prime numbers in reverse (descending) order. Observe that function BuildHeap performs no swaps because the original array is already a max-heap.

To emphasize the fact that Heapsort has the same time complexity for an N-element array whether or not it is nearly or completely sorted, when run with the resulting array in Figure 9 function BuildHeap performs 21 swaps and 42 comparisons, and the totals at the end of the sort are 108 swaps and 167 comparisons.
Since function HeapSort<T> is generic, Figure 10 shows the results of its execution of on an array of characters created from a character string.

5. Generic Smoothsort
This sorting algorithm, proposed by Edsger W. Dijkstra (EWD796a 1981) as an alternative to Heapsort, has been commented upon by several people. On the Stack Overflow site, it has been stated that the algorithm is not stable (a big word borrowed from Electrical Engineering and Control Theory) and that stability is more desirable than in-place sorting. Recall that an unstable sort does not preserve the order of identical elements (not a big deal for sorting purposes) and that Quicksort (another excellent sorting algorithm) is also unstable. So, the sorting in-place and the smooth transition from to execution time when an N-element array is nearly or completely sorted are excellent features of Smoothsort. On the other hand, it has been said that the resources on this algorithm are very scarce, and that those available are very hard to understand. As this section will demonstrate, Dijkstra’s design and implementation of Smoothsort are not hard to understand.
The author is aware of at least one implementation of Smoothsort in C++ (Schwarz 2011). After re-hashing the mathematics underlying its design, with some errors on the lengths of Leonardo sub-trees in two figures, Schwarz ends his article with a link to a smoothsort implementation of his own, that has nothing in common with Dijkstra’s code. The class name, global-variable names, and the function signatures in the GenericSmoothSort namespace implementing Dijkstra’s Smoothsort algorithm are shown in Figure 11.

Dijkstra’s code was written in what later became the formalism used by him and W.H.J. Feijen in their book A Method of Programming (Dijkstra and Feijen 1988). With the exception of functions Up and Down, the code in this section is almost a direct translation of Dijkstra’s code into C#. The comments on the right of the C# code reproduce the original code.
public static void SmoothSort<T>( T[] m ) where T : IComparable<T>
{
N = m.Length;
r1 = b1 = c1 = -1;
q = 1; r = 0; p = b = c = 1;
while ( q != N )
{
r1 = r;
if ( ( p % 8 ) == 3 )
{
b1 = b; c1 = c;
Sift( m );
p = ( p + 1 ) >> 2;
Up( ref b, ref c );
Up( ref b, ref c );
}
else if ( ( p % 4 ) == 1 )
{
if ( ( q + c ) < N )
{
b1 = b; c1 = c;
Sift( m );
}
else if ( ( q + c ) >= N )
{
Trinkle( m );
}
Down( ref b, ref c ); p <<= 1;
while ( b != 1 )
{
Down( ref b, ref c ); p <<= 1;
}
++p;
}
++q; ++r;
}
r1 = r; Trinkle( m );
while ( q != 1 )
{
--q;
if ( b == 1 )
{
--r; --p;
while ( UntypedUfn.IsEven( p ) )
{
p >>= 1;
Up( ref b, ref c );
}
}
else if ( b >= 3 )
{
--p; r = r - b + c;
if ( p == 0 )
{
}
else if ( p > 0 )
{
SemiTrinkle( m );
}
Down( ref b, ref c );
p = ( p << 1 ) + 1;
r = r + c;
SemiTrinkle( m );
Down( ref b, ref c );
p = ( p << 1 ) + 1;
}
}
}
This article is not the place to re-hash Dijkstra’s mathematics underlying his design of Smoothsort. The reader is best referred to his original description (Dijkstra 1981). For completeness sake, some of the terminology and the invariants maintained by the while loops in function SmoothSort are reproduced in Figure 12.

The beauty of Smoothsort is the re-arrangement of the array elements to create Leonardo trees in the first while loop. Leonardo trees are binary trees whose sizes are Leonardo numbers, which are the available stretch lengths (cf. EWD796a – 3), defined by the following recurrence relation.
$LP(0) = LP(1) = 1$
$LP(n+2)=LP(n+1)+LP(n)+1$
Quoting Dijkstra, ‘[f]or the sake of the recurrent stretch length computations, we introduce for each stretch length b its "companion" c, i.e., we maintain’
$(En:n\geq 0:b=LP(n) and c=LP(n-1)$
In words, there exists a positive integer n such that b and c are, respectively, the consecutive Leonardo numbers LP( n ) and LP( n - 1 ).
In a 0-based array, the root of a Leonardo tree of size LP( n ) nodes is at index LP( n ) – 1, its left child is at index LP( n – 1 ) – 1, and its right child is at index LP( n ) – 2. Thus, Dijkstra’s choice of Leonardo numbers guarantees that every parent node always has two children (cf. EWD796a – 7, Remark 2). As an illustration, Figures 13 and 14 show excerpts from the console output obtained by executing SmoothSort on the array of the first 25 prime numbers originally in descending order. The array declaration and the call to SmoothSort are as follows.
int[] a1 = { 97, 89, 83, 79, 73, 71, 67, 61, 59, 53, 47, 43, 41, 37, 31, 29, 23,
19, 17, 13, 11, 7, 5, 3, 2 },
TypedUfn<int>.SortArray( "Smooth Sort a1 (worst case)",
SmS.SmoothSort<int>, a1 );

The Leonardo tree shown in Figure 13 is invalid because two children exceed their parent. The designations "invalid" and "valid" for trees correspond to Dijkstra’s "dubious" and "trusty" designations (cf. EWD796a – 6) for stretches, that is, sequences of consecutive array elements. Figure 14 shows the state of the array and the Leonardo trees after swap 25.

The first while loop in function SmoothSort scans the array from left to right, and the second while loop scans it from right to left. Figure 15 illustrates the state of the array and the Leonardo tree just after swap 30.

The rest of this section provides the translation into C# of the additional functions implementing Smoothsort. The summary sections in their Intellisense comments reproduce Dijkstra’s descriptions.
Functions Up and Down subsume, respectively, functions up/up1 and down/down1 in the original code. The temporary variables in both functions are necessary because, as in the Algol programming language, the original functions used multiple assignment to variables and C# does not support it.
private static void Up( ref int b, ref int c )
{
int tmp1 = b + c + 1, tmp2 = b;
b = tmp1; c = tmp2;
}
private static void Down( ref int b, ref int c )
{
int tmp1 = c, tmp2 = b - c - 1;
b = tmp1; c = tmp2;
}
Functions Sift, Trinkle and SemiTrinkle implement the equivalent of the "reheap down" operation in HeapSort.
private static void Sift<T>( T[] m ) where T : IComparable<T>
{
while ( b1 >= 3 )
{
int r2 = r1 - b1 + c1, cmp;
cmp = m[ r2 ].CompareTo( m[ r1 - 1 ] );
if ( UntypedUfn.IsGE( cmp ) )
{
}
else if ( UntypedUfn.IsLE( cmp ) )
{
r2 = r1 - 1;
Down( ref b1, ref c1 );
}
cmp = m[ r1 ].CompareTo( m[ r2 ] );
if ( UntypedUfn.IsGE( cmp ) )
{
b1 = 1;
}
else if ( UntypedUfn.IsLT( cmp ) )
{
TypedUfn<T>.Swap( " Sift",
m, r1, r2 );
DisplayState( m );
r1 = r2;
Down( ref b1, ref c1 );
}
}
}
private static void Trinkle<T>( T[] m ) where T : IComparable<T>
{
int p1 = p; b1 = b; c1 = c;
while ( p1 > 0 )
{
int r3;
while ( UntypedUfn.IsEven( p1 ) )
{
p1 >>= 1;
Up( ref b1, ref c1 );
}
r3 = r1 - b1;
int cmp;
if ( p1 == 1
||
UntypedUfn.IsLE(
(cmp
= m[ r3 ].CompareTo( m[ r1 ] )) ) )
{
p1 = 0;
}
else if ( p1 > 1 && UntypedUfn.IsGT( cmp ) )
{
--p1;
if ( b1 == 1 )
{
TypedUfn<T>.Swap( " Trinkle",
m, r1, r3 );
DisplayState( m );
r1 = r3;
}
else if ( b1 >= 3 )
{
int r2 = r1 - b1 + c1;
cmp
= m[ r2 ].CompareTo( m[ r1 - 1 ] );
if ( UntypedUfn.IsGE( cmp ) )
{
}
else if ( UntypedUfn.IsLE( cmp ) )
{
r2 = r1 - 1;
Down( ref b1, ref c1 );
p1 <<= 1;
}
cmp = m[ r3 ].CompareTo( m[ r2 ] );
if ( UntypedUfn.IsGE( cmp ) )
{
TypedUfn<T>.Swap( " Trinkle",
m, r1, r3 );
DisplayState( m );
r1 = r3;
}
else if ( UntypedUfn.IsLE( cmp ) )
{
TypedUfn<T>.Swap( " Trinkle",
m, r1, r2 );
DisplayState( m );
r1 = r2;
Down( ref b1, ref c1 );
p1 = 0;
}
}
}
}
Sift( m );
}
private static void SemiTrinkle<T>( T[] m ) where T : IComparable<T>
{
r1 = r - c;
int cmp = m[ r1 ].CompareTo( m[ r ] );
if ( UntypedUfn.IsLE( cmp ) )
{
}
else if ( UntypedUfn.IsGT( cmp ) )
{
TypedUfn<T>.Swap( "SemiTrinkle",
m, r, r1 );
DisplayState( m );
Trinkle( m );
}
}
There are two functions which were not in Dijkstra’s original code. They are used to display on the console the state variables (b, c, p, r, q) of SmoothSort and, as shown in Figures 13, 14 and 15, information on the Leonardo trees that occur in the array being sorted.
private static void DisplayState<T>( T[] m ) where T : IComparable<T>
{
LPtree<T> tree = new LPtree<T>( m, b, c );
if ( Uvar.outMode == OutMode.verbose )
{
DisplayVars();
}
tree.TrySaveAndDisplay();
}
private static void DisplayVars()
{
int idx, k = LPfn.InvLP( b );
string fmtStr1 = Uvar.elementFormat, fmtStr2 = "LP({0})";
UntypedUfn.SkipOB( out idx ); UntypedUfn.DisplayStr( " ", ref idx, b );
Console.Write( fmtStr1, "b" );
Console.WriteLine( fmtStr2, k );
UntypedUfn.SkipOB( out idx ); UntypedUfn.DisplayStr( " ", ref idx, c );
Console.Write( fmtStr1, "c" );
Console.WriteLine( fmtStr2, k - 1 );
Console.WriteLine( "p: {0} ({1})", p, UntypedUfn.ToBinaryStr( p ) );
UntypedUfn.SkipOB( out idx ); UntypedUfn.DisplayStr( " ", ref idx, r );
Console.Write( fmtStr1, "r" );
Console.WriteLine( fmtStr1, "q" );
Console.WriteLine();
}
As a final example in this section, Figures 16a and 16b show the state of an array containing the first 50 prime numbers, originally in descending order, just before and after swap 45.


6. Smoothsort vs. Heapsort
An array that initially is in descending order represents a worst-case scenario for any algorithm that sorts elements in ascending order. In the example of the first 50 prime numbers, upon termination, SmoothSort performed 223 swaps and 1323 comparisons, while HeapSort performed 207 swaps and 379 comparisons. Figure 17 shows the declarations of five sample integer arrays, the templates for the calls to SmoothSort and HeapSort, and a table of the number of swaps and comparisons performed in each case. Clearly, SmoothSort outperforms HeapSort when the original array is nearly or completely sorted.

7. Utility Functions
The library UtilSortLib contains typed and untyped functions that are common to sorting algorithms. The typed functions are in class TypedUfn<T> and the untyped ones are in class UntypedUfn. The most important typed function is the one called to sort an array using a reference to a particular sorting function, whose signature must adhere to the delegate specification.
public delegate void SortingFunction( T[] arr );
public static void SortArray( string msg, SortingFunction SortFn, T[] arr,
OutMode mode = OutMode.quiet, bool dispTree = false )
{
SetVariables( arr, mode );
Console.WriteLine();
if ( ! String.IsNullOrEmpty( msg ) )
{
Console.WriteLine( "{0}\n", msg );
}
if ( dispTree )
{
TypedUfn<T>.DisplayTree( "before " + msg, arr );
}
DisplayArray( "Original", arr ); Console.WriteLine();
SortFn( arr );
DisplayArray( "Sorted", arr );
if ( dispTree )
{
TypedUfn<T>.DisplayTree( "after " + msg, arr );
}
Console.WriteLine( "\n{0} swaps; {1} comparisons",
Uvar.swapCount, Uvar.compCount );
Console.WriteLine();
}
Function SetVariables is called to initialize the global variables used for display purposes during sorting. As indicated, this function must be called before calling functions DisplayArray and/or DisplayTree for the first time.
public static void SetVariables( T[] arr, OutMode mode )
{
Uvar.elementWidth = MaxElementWidth( arr );
Uvar.elementFormat
= "{0"
+ String.Format( ",{0}", Uvar.elementWidth )
+ "} ";
Uvar.elementParams
= String.Format( "\nElement width: {0}, element format string: '{1}'",
Uvar.elementWidth, Uvar.elementFormat );
Uvar.swapCount = 0;
Uvar.compCount = 0;
Uvar.outMode = mode;
}
Since the sorting function is expected to handle generic arrays, function MaxElementWidth is called to determine the maximum array-element width to be used for proper formatting during display.
private static int MaxElementWidth( T[] arr )
{
int maxWidth = int.MinValue;
if ( arr[ 0 ] is char )
{
maxWidth = 3;
}
else
{
int N = arr.Length, width = 0;
for ( int i = 0; i < N; ++i )
{
string str = arr[ i ].ToString();
width = str.Length;
if ( width > maxWidth )
{
maxWidth = width;
}
}
if ( arr[ 0 ] is string )
{
maxWidth += 2;
}
}
return maxWidth;
}
There are two versions of function Swap. The first one just takes two reference arguments and exchanges them. The second is the one that usually should be called in case the swap operation is to be displayed on the console, as illustrated in Figures 13, 14 and 15.
public static void Swap( ref T x, ref T y )
{
T tmp = x;
x = y; y = tmp;
}
public static void Swap( string fName, T[] m, int i, int j )
{
++Uvar.swapCount;
if ( Uvar.outMode == OutMode.verbose )
{
TypedUfn<T>.DisplayArray( "", m );
DisplaySwap( fName, m, i, j );
}
Swap( ref m[ i ], ref m[ j ] );
}
public static void DisplaySwap( string fName, T[] m, int idx1, int idx2 )
{
int k, _1st, _2nd;
if ( idx1 > idx2 )
{
_1st = idx2; _2nd = idx1;
}
else
{
_1st = idx1; _2nd = idx2;
}
UntypedUfn.SkipOB( out k ); UntypedUfn.DisplayStr( " ", ref k, _1st );
Console.Write( Uvar.elementFormat, "↑" );
++k;
UntypedUfn.DisplayStr( " ", ref k, _2nd );
Console.WriteLine( Uvar.elementFormat, "↑" );
Console.WriteLine(
"\t{0}: swap( m[ {1,2} ]:{2,2}, m[ {3,2} ]:{4,2} ), swapCount: {5}\n",
fName, idx1, ElementToString( m, idx1 ), idx2, ElementToString( m, idx2 ),
Uvar.swapCount );
}
Two of the last four typed utility functions are DisplayArray to display on the console an array in linear form, and DisplayTree to display an array as a binary tree. Both functions take care of displaying array elements in a suitable format, the second one also taking care of the spacing of tree nodes. Function DisplayArray calls function DisplayIndices to show the indices above the array elements.
public static void DisplayArray( string msg, T[] arr, string leadSpace = "" )
{
int N = arr.Length;
if ( !String.IsNullOrEmpty( msg ) )
{
Console.WriteLine( "\n{0} array:\n", msg );
}
DisplayIndices( N, leadSpace );
if ( !String.IsNullOrEmpty( leadSpace ) )
{
Console.Write( leadSpace );
}
Console.Write( "[ " );
for ( int i = 0; i < N; ++i )
{
Console.Write( Uvar.elementFormat, ElementToString( arr, i ) );
}
Console.WriteLine( "]" );
}
private static void DisplayIndices( int N, string leadSpace = "" )
{
if ( !String.IsNullOrEmpty( leadSpace ) )
{
Console.Write( leadSpace );
}
Console.Write( " " );
for ( int i = 0; i < N; ++i )
{
Console.Write( Uvar.elementFormat, i );
}
Console.WriteLine();
}
public static void DisplayTree( string msg, T[] a )
{
if ( !String.IsNullOrEmpty( msg ) )
{
Console.WriteLine( "\nTree {0}:", msg );
}
int N = a.Length,
maxLevel,
level = 0,
nodes = 1,
leadSp = UntypedUfn.CeilPof2forTree( N, out maxLevel ),
elemSp = 0;
int k = 0;
do
{
Console.WriteLine();
UntypedUfn.Spaces( leadSp );
for ( int j = 1; j <= nodes && k < N; ++j )
{
Console.Write( Uvar.elementFormat, ElementToString( a, k ) );
++k;
UntypedUfn.Spaces( elemSp - 2 );
}
Console.WriteLine( "\n" );
elemSp = leadSp;
leadSp >>= 1;
++level;
nodes <<= 1;
} while ( level <= maxLevel );
Console.WriteLine();
}
Both DisplayArray and DisplayTree call function ElementToString to account for the cases when array elements are of type char or string. Observe that if the array elements are of a non-primitive data type the definition of such type must override function ToString, and must implement an integer-valued CompareTo function.
public static string ElementToString( T[] arr, int i )
{
string str = arr[ i ].ToString();
if ( arr[ i ] is char )
{
return Uvar._1quote + str + Uvar._1quote;
}
if ( arr[ i ] is string )
{
return Uvar._2quote + str + Uvar._2quote;
}
return str;
}
Finally, function DisplayTree calls function UntypedUfn.CeilPof2forTree to compute the smallest power of two for a perfect tree that can contain a given number of nodes, and the maximum level of such a tree. Those numbers are used in the spacing and the display of nodes per level of the tree.
public static int CeilPof2forTree( int nodes, out int maxLevel )
{
maxLevel = 0;
int pOf2 = 1,
sum = 1;
while ( sum < nodes )
{
++maxLevel;
pOf2 <<= 1;
sum += pOf2;
}
return pOf2;
}
Most of the untyped utility functions (in class UntypedUfn) are self-explanatory via their Intellisense comments and will not be described here.
8. Sorting Other Data Types
In this section, SmoothSort is shown to be able to handle arbitrary data types. To begin with, consider sorting an array of characters. The following code is suitable to provide a simple example. Observe that the values of the two optional arguments to function SortArray have been overridden.
string str2 = "a sample string";
char[] c2 = str2.ToCharArray();
TypedUfn<char>.SortArray( "Smooth Sort c2", SmS.SmoothSort<char>, c2,
OutMode.verbose, true );
The execution of SortArray with the given arguments produces a lot of console output. The array is displayed as a tree before and after the sort, the calls to function Swap are documented, and the state variables (b, c, p, r, q) and unique Leonardo trees are displayed after each swap. Figure 18 shows excerpts from the console output.

In order to demonstrate the sorting of elements from an arbitrary data type, consider the definition of a class to represent points in the two-dimensional, integer x-y plane. (The author is aware of the struct Point defined in the System.Drawing namespace. However, that struct does not define a CompareTo function, which is what was needed to be illustrated for a user-defined data type.)
public class _2Dpoint : IComparable<_2Dpoint>
{
private int x, y;
public _2Dpoint( int _x, int _y )
{
x = _x; y = _y;
}
public override string ToString()
{
return String.Format( "({0} {1})", x, y );
}
public int CompareTo( _2Dpoint p )
{
return ( x < p.x || ( x == p.x && y < p.y ) )
? -1
: ( x == p.x && y == p.y ) ? 0 : 1;
}
public static _2Dpoint[] _2DpointArray( params int[] xyPairs )
{
int n = xyPairs.Length;
if ( ( n % 2 ) != 0 )
{
throw new Exception( "_2DpointArray: argument list length must be even" );
}
_2Dpoint[] arr = new _2Dpoint[ n >> 1 ];
int i = 0, j = 0;
while ( i < n )
{
arr[ j ] = new _2Dpoint( xyPairs[ i ], xyPairs[ i + 1 ] );
i += 2;
++j;
}
return arr;
}
}
The class _2Dpoint is very simple. It defines the basic constructor, overrides function ToString and, most importantly, defines the required integer-valued CompareTo function for sorting purposes. The comparison of two points is done according to lexicographic ordering. The class also defines a static function to generate an array of _2Dpoint instances. Such a function expects a series of pairs of numbers defining points.
The following code creates an array of 13 points, and applies SmoothSort to the array. Figure 19 shows excerpts from the console output. Observe that instances of class _2Dpoint are shown inside braces, as in {3 0}, to avoid confusion with their encoding with LP_Index instances, as with ( 1 6). (This is shown by red highlighting.)
_2Dpoint[] g = _2Dpoint._2DpointArray(
8, 3, 5, 5, 4, 1, 1, 9, 5, 4, 1, 0,
4, 4, 3, 0, 4, 2, 4, 1, 1, 0, 0, 0, -1, 0 );
TypedUfn<_2Dpoint>.SortArray( "Smooth Sort g", SmS.SmoothSort<_2Dpoint>, g, OutMode.verbose );

9. Functions on Leonardo Numbers and Leonardo Trees
By Dijkstra’s design, Leonardo numbers and trees are an integral part of Smoothsort. The class library LPlib contains several classes and a lot of functions to deal with Leonardo numbers and Leonardo trees. For ease of testing and editing, they were written within the GenericSmoothSort namespace but now they reside in a library of their own. The classes and their functions will be presented in the order of their development.
It should be noted that the LPlib functionality is NOT necessary for the execution of SmoothSort. If all the calls to function DisplayState after each call to Swap in file SmS.cs were commented out, the LP-related classes and functions would not be needed and the sort would work as expected. They are used solely to document on the console the operation of SmoothSort. So, the reader may skip this section if so desired.
9.1. Class LPfn
This static class contains a static variable and static functions related to Leonardo numbers. Function LP computes if necessary and returns a Leonardo number. As stated in Section 5, Leonardo numbers are defined by the following recurrence relation:
$LP(0) = LP(1) = 1$
$LP(n+2)=LP(n+1)+LP(n)+1$
Function LP is memoized by the use of a list of Leonardo numbers, Lpnumber, whose count of elements can increase during execution. As a consequence, Leonardo numbers are not computed recursively and are generated on demand.
private static List<int> LPnumber = new List<int>() { 1, 1, 3 };
public static int LP( int k )
{
if ( k < 0 )
{
return -1;
}
else
{
int n = LPnumber.Count - 1;
while ( n < k )
{
LPnumber.Add( LPnumber[ n ] + LPnumber[ n - 1 ] + 1 );
++n;
}
return LPnumber[ k ];
}
}
Function InvLP computes the inverse, that is, the index, of a Leonardo number if it exists. This function is not strictly necessary, for it has been used only once (by function SmS.DisplayVars) for display purposes.
public static int InvLP( int lp )
{
int i = -1;
if ( lp > 0 )
{
int n = LPnumber.Count;
i = 1;
while ( ( i < n ) && ( LPnumber[ i ] != lp ) )
{
if ( LPnumber[ i ] > lp )
{
break;
}
++i;
}
}
return i;
}
There are two versions of a function (LPnumbers) to compute two consecutive Leonardo numbers. The first one determines an index n such that the values of the global variables b and c in SmoothSort are equal to two consecutive Leonardo numbers indexed by n (cf. EWD796a – 3). The second, computes two consecutive Leonardo numbers given the index of the larger one.
public static int LPnumbers( int b, int c )
{
int n = 0, LPn = 1, LPn_1 = -1;
while ( !( n > b ) && !( LPn == b && LPn_1 == c ) )
{
++n;
int tmp = LPn;
LPn = LPn + LPn_1 + 1;
LPn_1 = tmp;
}
if ( n > b )
{
n = -1; LPn = -1; LPn_1 = -1;
}
return n;
}
public static void LPnumbers( int k, out int LPn, out int LPn_1 )
{
int n = 0; LPn = 1; LPn_1 = -1;
while ( n < k )
{
++n;
int tmp = LPn;
LPn = LPn + LPn_1 + 1;
LPn_1 = tmp;
}
}
9.2. Class LP_Index
This class encapsulates a Leonardo number and an index into an array. It is the basic building block for encoding nodes of a Leonardo tree. The class overrides function ToString, and provides a CompareTo function and a function to determine if an encoding trivially corresponds to a singleton node.
public class LP_Index
{
private int lp;
private int index;
public int LP { get { return lp; } }
public int Index { get { return index; } }
public LP_Index( int _lp, int _index )
{
lp = _lp;
index = _index;
}
public override string ToString()
{
return String.Format( "({0,2} {1,2})", lp, index );
}
public int CompareTo( LP_Index other )
{
if ( (lp < other.lp ) || ( lp == other.lp && index < other.index ) )
{
return -1;
}
if ( lp == other.lp && index == other.index )
{
return 0;
}
return +1;
}
public bool Is_Singleton()
{
return lp == 1;
}
}
9.3. Class LPtriple
This class encapsulates three LP_Index instances that encode nodes of a Leonardo tree: a left child, a right child and their parent. Instances of this class are used by class LPtree to describe the Leonardo trees over a span of the array being sorted, as delimited by global variable b and its "companion" c in SmoothSort.
public class LPtriple<T> where T : IComparable<T>
{
private LP_Index parent, leftChild, rightChild;
private string pKey, lChKey, rChKey;
private string strRepr;
public LPtriple()
{
parent = leftChild = rightChild = null;
pKey = lChKey = rChKey = null;
Displayed = false;
strRepr = null;
}
public LPtriple( params int[] pairs )
{
parent = leftChild = rightChild = null;
pKey = lChKey = rChKey = null;
if ( pairs.Length != 6 )
{
throw new Exception( "LPtriple constructor: 6 {int} parameters expected" );
}
parent = new LP_Index( pairs[ 0 ], pairs[ 1 ] );
leftChild = new LP_Index( pairs[ 2 ], pairs[ 3 ] );
rightChild = new LP_Index( pairs[ 4 ], pairs[ 5 ] );
Displayed = false;
pKey = parent.ToString();
lChKey = leftChild.ToString();
rChKey = rightChild.ToString();
strRepr = ToString();
}
public LP_Index Parent { get { return parent; } }
public LP_Index LeftChild { get { return leftChild; } }
public LP_Index RightChild { get { return rightChild; } }
public string ParentKey { get { return pKey; } }
public string LchildKey { get { return lChKey; } }
public string RchildKey { get { return rChKey; } }
public bool Displayed { get; set; }
public int Width { get { return strRepr.Length; } }
public string StrRepr { get { return strRepr; } }
public override string ToString()
{
return String.Format( "< {0} {1} {2} >",
LchildKey, RchildKey, ParentKey,
Displayed ? " *" : "" );
}
public string ToLongString( T[] m )
{
return String.Format( "< {0}: {1}, {2}: {3}, {4}: {5} >{6}",
LchildKey, TypedUfn<T>.ElementToString( m, leftChild.Index ),
RchildKey, TypedUfn<T>.ElementToString( m, rightChild.Index ),
ParentKey, TypedUfn<T>.ElementToString( m, parent.Index ),
Displayed ? " *" : "" );
}
public LPtriple<T> Copy()
{
LPtriple<T> _copy = new LPtriple<T>();
_copy.parent = this.parent;
_copy.leftChild = this.leftChild;
_copy.rightChild = this.rightChild;
_copy.pKey = this.pKey;
_copy.lChKey = this.lChKey;
_copy.rChKey = this.rChKey;
_copy.strRepr = this.strRepr;
_copy.Displayed = this.Displayed;
return _copy;
}
public bool IsValid( T[] m )
{
return UntypedUfn.IsLE( m[ leftChild.Index ].CompareTo( m[ parent.Index ] ) )
&&
UntypedUfn.IsLE( m[ rightChild.Index ].CompareTo( m[ parent.Index ] ) );
}
}
The class overrides the standard ToString function and provides a function ToLongString which includes the values of the array elements indexed by the triple, and an asterisk if the triple has been displayed on the console. There is a Copy constructor and a function to determine whether or not a triple encodes a valid Leonardo tree or sub-tree, that is, whether the children do not exceed their parent.
9.4. Classes LPvar and LPtree
The static class LPvar contains a one-time global variable that was removed from SmoothSort because there was no reason for it to be there since it was not used in Dijkstra’s original code.
using System;
using System.Collections.Generic;
namespace LPlib
{
public static class LPvar
{
public static List<Dictionary<string, string[]>> nodeValuesDictList = null;
}
}
Variable nodeValuesDictList is used to keep track of dictionaries generated during the execution of SmoothSort to prevent displaying trees or sub-trees that already have been displayed. A natural choice would have been to use instances of the LP_Index class as dictionary keys. However, they cannot be used because the Dictionary class in C# computes hash codes for the keys, and can only apply hashing to primitive data types. Therefore, the string representations of LP_Index instances were used as dictionary keys. Since the class LPtree has several fields and many functions, they will be described separately.
The class LPtree contains several private fields, declared in the following partial description.
using System;
using System.Collections.Generic;
using UtilSortLib;
namespace LPlib
{
public class LPtree<T> where T : IComparable<T>
{
private T[] mSnap;
private int b, c;
private List<List<LPtriple<T>>>
cTriples,
bTriples;
private string cBounds, bBounds;
private LP_Index rootNode;
private Dictionary<string, LPtriple<T>> triplesDict;
private Dictionary<string, string[]> nodeValuesDict;
private Queue<LP_Index> nodeQueue;
...
}
}
The class constructor initializes all the fields and the single global variable LPvar.nodeValuesDictList on the first call. Since this constructor is called by function SmS.DisplayState after each call to TypedUfn<T>.Swap, it takes as arguments the current state of the array being sorted and the values of the global variables b and c in SmoothSort. Then it ends by calling GenerateTriples to generate the triples in the half-open intervals [ 0, c ) and [ c, b ) over the array.
public LPtree( T[] _m, int _b, int _c )
{
mSnap = new T[ _m.Length ];
_m.CopyTo( mSnap, 0 );
b = _b; c = _c;
if ( LPvar.nodeValuesDictList == null )
{
LPvar.nodeValuesDictList = new List<Dictionary<string, string[]>>();
}
cTriples = new List<List<LPtriple<T>>>();
bTriples = new List<List<LPtriple<T>>>();
cBounds = bBounds = String.Empty;
triplesDict
= new Dictionary<string, LPtriple<T>>();
nodeValuesDict
= new Dictionary<string, string[]>();
rootNode = null;
nodeQueue = null;
GenerateTriples();
}
Triples are generated over the specified intervals as long as c is greater than 1 and then if b – c is greater than 2. They are generated by function IntervalTriples, and added to two dictionaries by function AddToDictionaries. This last function returns the LP_Index encoding of the root node of a "b-c" Leonardo tree.
private void GenerateTriples()
{
triplesDict = new Dictionary<string, LPtriple<T>>();
rootNode = null;
int i = LPfn.InvLP( c );
if ( c > 1 )
{
cTriples = IntervalTriples( 0, c );
cBounds = String.Format( "[{0}, {1})", 0, c );
AddNewList( RootTriple( i, c ), cTriples );
rootNode = AddToDictionaries( cTriples, triplesDict );
}
if ( ( b - c ) > 2 )
{
bTriples = IntervalTriples( c, b );
bBounds = String.Format( "[{0}, {1})", c, b );
++i;
AddNewList( RootTriple( i, b ), bTriples );
rootNode = AddToDictionaries( bTriples, triplesDict );
}
nodeQueue = new Queue<LP_Index>();
if ( rootNode != null )
{
nodeQueue.Enqueue( rootNode );
}
}
Function IntervalTriples generates a list of LPtriple lists over a half-open interval of the array being sorted. The reason for creating a list of lists is that some triples encode nodes at an upper level in the tree hierarchy and other triples encode nodes at the same level as other nodes. Figure 20 shows an example of both cases.
private List<List<LPtriple<T>>> IntervalTriples( int lb, int ub )
{
List<List<LPtriple<T>>> listOfTriplesLists = new List<List<LPtriple<T>>>();
int i = 1,
LPi = LPfn.LP( i ),
k = lb;
LPtriple<T> triple0 = new LPtriple<T>(), triple1 = new LPtriple<T>();
while ( LPi < ub )
{
++i;
LPi = LPfn.LP( i );
if ( lb + LPi >= ub )
{
break;
}
k = lb + LPi - 1;
MakeNewTriple( i, k, ref triple0, ref triple1, listOfTriplesLists );
};
i = 1;
while ( k < ub )
{
++i;
LPi = LPfn.LP( i );
k += LPi;
if ( k >= ub )
{
break;
}
MakeNewTriple( i, k, ref triple0, ref triple1, listOfTriplesLists );
};
return listOfTriplesLists;
}

The decision to create a new level of triples or to extend a list of triples at the current last level is carried out by function MakeNewTriple, which calls either AddNewList or ExtendLastList to perform those tasks.
private void MakeNewTriple( int i, int k,
ref LPtriple<T> triple0, ref LPtriple<T> triple1,
List<List<LPtriple<T>>> listOfTriplesLists )
{
triple0 = triple1.Copy();
triple1
= new LPtriple<T>( LPfn.LP( i ), k,
LPfn.LP( i - 1 ), k - 2,
LPfn.LP( i - 2 ), k - 1 );
if ( ( listOfTriplesLists.Count == 0 )
||
UntypedUfn.IsEQ(
mSnap[ triple1.LeftChild.Index ].CompareTo( mSnap[ triple0.Parent.Index ] ) ) )
{
AddNewList( triple1, listOfTriplesLists );
}
else
{
ExtendLastList( listOfTriplesLists, triple1 );
}
}
private void AddNewList( LPtriple<T> triple, List<List<LPtriple<T>>> listOfTriplesLists )
{
List<LPtriple<T>> tripleList = new List<LPtriple<T>>();
tripleList.Add( triple );
listOfTriplesLists.Add( tripleList );
}
private void ExtendLastList( List<List<LPtriple<T>>> listOfTriplesLists, LPtriple<T> triple )
{
List<LPtriple<T>> tripleList = listOfTriplesLists[ listOfTriplesLists.Count - 1 ];
tripleList.Add( triple );
}
Function RootTriple is called by GenerateTriples to create the root-node triple for the generated lists of c- and b-triples, adding a new list with that node.
private LPtriple<T> RootTriple( int i, int k )
{
int LPi_1 = LPfn.LP( i - 1 );
return new LPtriple<T>( LPfn.LP( i ), k - 1,
LPi_1, LPi_1 - 1,
LPfn.LP( i - 2 ), k - 2 );
}
When the lists of c- and b-triples are complete, function AddToDictionaries is called to add the triples from each list to the dictionary of triples that will be used to display Leonardo trees, and to the dictionary nodeValuesDict which is used to avoid displaying Leonardo trees more than once. The string representation of the LP_Index coding of the parent from each triple is used as the key in both dictionaries. The values in the first dictionary are triples, while in the second the values are arrays containing the string representations of the indexed elements from the snapshot (mSnap) of the array being sorted.
private LP_Index AddToDictionaries( List<List<LPtriple<T>>> listOfTriplesLists,
Dictionary<string, LPtriple<T>> dictionary )
{
LPtriple<T> lastTriple = null;
foreach ( List<LPtriple<T>> triplesList in listOfTriplesLists )
{
foreach ( LPtriple<T> triple in triplesList )
{
string key = triple.Parent.ToString();
dictionary.Add( key, triple );
string[] valueArr =
new string[ 3 ] { mSnap[ triple.LeftChild.Index ].ToString(),
mSnap[ triple.RightChild.Index ].ToString(),
mSnap[ triple.Parent.Index ].ToString() };
nodeValuesDict.Add( key, valueArr );
lastTriple = triple;
}
}
return lastTriple == null ? null : lastTriple.Parent;
}
As mentioned in the caption of Figure 20, if the value of the optional argument to function TrySaveAndDisplay is true, the c- and b-triples are displayed on the console by calling function DisplayTriples. Then, if there are nodes to be displayed and if the dictionary nodeValuesDict is not in LPvar.nodeValuesDictList (the global dictionary list) it is added to that list, and the Leonardo tree(s) are displayed, starting with the tree spanned by the c and b sub-trees and continuing with the disjoint trees.
public void TrySaveAndDisplay( bool dispTriples = false )
{
if ( triplesDict.Count > 0 )
{
if ( dispTriples )
{
if ( cTriples.Count > 0 )
{
DisplayTriples( "c", cBounds, cTriples );
if ( bTriples.Count > 0 )
{
DisplayTriples( "b", bBounds, bTriples );
}
}
}
if ( ( nodeQueue.Count > 0 ) )
{
if ( !InDictionaryList( LPvar.nodeValuesDictList ) )
{
LPvar.nodeValuesDictList.Add( nodeValuesDict );
DisplayLabels( triplesDict );
DisplayNodes( nodeQueue, triplesDict );
DisplayDisjointTrees( triplesDict );
}
}
}
}
Function DisplayTriples is called by TrySaveAndDisplay to display the lists of c and b triples. Function InDictionaryList determines, with the help of functions SubTreeOf and SameElementValues, whether a dictionary of node values is in the global list of dictionaries. The Intellisense comments of those functions are pretty much self- explanatory.
private void DisplayTriples( string name, string bounds,
List<List<LPtriple<T>>> listOfTriplesLists )
{
Console.WriteLine( "\n{0} sub-tree triples {1} :\n", name, bounds );
foreach ( List<LPtriple<T>> triplesList in listOfTriplesLists )
{
foreach ( LPtriple<T> triple in triplesList )
{
Console.Write( triple.ToLongString( mSnap ) );
Console.Write( " " );
}
Console.WriteLine();
}
}
private bool InDictionaryList( List<Dictionary<string, string[]>> nodeValsDictList )
{
bool inList = false;
if ( nodeValsDictList.Count > 0 )
{
foreach ( Dictionary<string, string[]> otherDict in nodeValsDictList )
{
if ( SubTreeOf( otherDict ) )
{
inList = true; break;
}
}
}
return inList;
}
private bool SubTreeOf( Dictionary<string, string[]> otherDict )
{
foreach ( KeyValuePair<string, string[]> kvp in nodeValuesDict )
{
if ( otherDict.ContainsKey( kvp.Key ) )
{
if ( !SameElementValues( kvp.Value, otherDict[ kvp.Key ] ) )
{
return false;
}
}
else
{
return false;
}
}
return true;
}
private bool SameElementValues( string[] idxArr1, string[] idxArr2 )
{
return idxArr1[ 0 ].Equals( idxArr2[ 0 ] )
&&
idxArr1[ 1 ].Equals( idxArr2[ 1 ] )
&&
idxArr1[ 2 ].Equals( idxArr2[ 2 ] );
}
If a dictionary of node values is not in the global list, function TrySaveAndDisplay adds it to the list and calls DisplayLabels to display, with some leading space, the snap of the array being sorted and, one line at a time, a triple of node encodings and labels ("L", "R" and "↑") to mark the left-child, right-child and root nodes of Leonardo trees encoded by the triple. The leading space is computed by function MaxTripleWidth.
private void DisplayLabels( Dictionary<string, LPtriple<T>> dictionary )
{
string fmtStr = Uvar.elementFormat,
leadSpFmt = "{0," + MaxTripleWidth( dictionary ).ToString() + "}",
leadSpace = String.Format( leadSpFmt, " " );
Console.WriteLine();
TypedUfn<T>.DisplayArray( "", mSnap, leadSpace );
foreach ( KeyValuePair<string, LPtriple<T>> kvp in dictionary )
{
LPtriple<T> triple = kvp.Value;
int idx;
Console.Write( triple.StrRepr );
UntypedUfn.SkipOB( out idx );
UntypedUfn.DisplayStr( " ", ref idx, triple.LeftChild.Index );
Console.Write( fmtStr, "L" );
UntypedUfn.DisplayStr( " ", ref idx, triple.RightChild.Index - 1 );
Console.Write( fmtStr, "R" );
UntypedUfn.DisplayStr( " ", ref idx, triple.Parent.Index - 2 );
Console.WriteLine( fmtStr, "↑" );
}
Console.WriteLine();
}
private static int MaxTripleWidth( Dictionary<string, LPtriple<T>> dictionary )
{
int maxWidth = 0;
foreach ( KeyValuePair<string, LPtriple<T>> kvp in dictionary )
{
LPtriple<T> triple = kvp.Value;
if ( triple.Width > maxWidth )
{
maxWidth = triple.Width;
}
}
return maxWidth;
}
The last two functions called by TrySaveAndDisplay are DisplayNodes and DisplayDisjointTrees. The first is very similar to function DisplayTree in class TypedUfn<T> of UtilSortLib, but it uses queues to handle the level-by-level traversal of a tree (that is, the technique used in breadth-first search). After displaying the "b-c" Leonardo tree, function DisplayDisjointTrees is called to display any trees not accessible by that tree, as illustrated in Figures 14, 16a and 16b.
private void DisplayNodes( Queue<LP_Index> nodeQueue,
Dictionary<string, LPtriple<T>> dictionary )
{
int maxLevel,
leadSp = UntypedUfn.CeilPof2forTree( 2 * dictionary.Count + 2,
out maxLevel ),
elemSp = 0;
bool valid = true;
Queue<LP_Index> childrenQueue;
List<string> absentKeys = new List<string>();
Console.WriteLine();
do
{
UntypedUfn.Spaces( leadSp );
childrenQueue = new Queue<LP_Index>();
while ( nodeQueue.Count > 0 )
{
LP_Index node = nodeQueue.Dequeue();
string key = node.ToString();
Console.Write( Uvar.elementFormat,
TypedUfn<T>.ElementToString( mSnap, node.Index ) );
UntypedUfn.Spaces( elemSp - 2 );
if ( dictionary.ContainsKey( key ) )
{
LPtriple<T> triple = dictionary[ node.ToString() ];
childrenQueue.Enqueue( triple.LeftChild );
childrenQueue.Enqueue( triple.RightChild );
if ( valid )
{
valid = triple.IsValid( mSnap );
}
triple.Displayed = true;
}
else if ( !node.Is_Singleton() )
{
absentKeys.Add( key );
}
}
Console.WriteLine( "\n\n" );
if ( childrenQueue.Count > 0 )
{
nodeQueue = childrenQueue;
elemSp = leadSp;
leadSp >>= 1;
}
} while ( childrenQueue.Count > 0 );
Console.WriteLine( "{0} Leonardo tree\n", valid ? "Valid" : "Invalid" );
}
private void DisplayDisjointTrees( Dictionary<string, LPtriple<T>> dictionary )
{
Dictionary<string, LPtriple<T>> subDict;
Queue<LP_Index> nodeQueue;
LP_Index lastParent;
do
{
subDict = new Dictionary<string, LPtriple<T>>();
nodeQueue = new Queue<LP_Index>();
lastParent = null;
foreach ( KeyValuePair<string, LPtriple<T>> kvp in dictionary )
{
LPtriple<T> triple = kvp.Value;
if ( !triple.Displayed )
{
subDict.Add( kvp.Key, kvp.Value );
lastParent = triple.Parent;
}
}
if ( lastParent != null )
{
nodeQueue.Enqueue( lastParent );
DisplayNodes( nodeQueue, subDict );
}
} while ( lastParent != null );
}
10. Conclusion
This article has presented an almost literal translation into C# of Edsger W. Dijkstra’s Smoothsort algorithm. It was implemented as a collection of generic C# functions. Since Smoothsort was proposed as an alternative to Heapsort for sorting in place, a generic implementation of the latter in C# was also presented. Both algorithms were tested on integer and character data types, and on instances of a class to handle points on the integer x-y plane. In sample executions, Smoothsort was shown to outperform Heapsort when the original array is nearly or completely sorted.
11. Using the Code
The code described in this article is in several directories. The paths for the directories are listed and explained in Figure 21, as the code was stored in a USB drive with drive letter "F:". Each of the terminal directories in the paths contains a complete Visual Studio solution, so that the code is ready to use. The solutions under the TESTS directory (TestHeapSort and TestSmoothSort) are console applications. All the other solutions are libraries, which cannot be executed by themselves. The test applications provide examples of how to use the code, and can be run without changes to the libraries. Most of the examples are commented out and the reader can uncomment particular ones to run tests of the sorting algorithms.

If any changes are made in the libraries, they should be re-built. Libraries _2DpointsLib and UtilSortLib are independent from each other and can be built in any order, but they MUST be built before GenericHeapSort. Library LPlib must be built after UtilSortLib and before GenericSmoothSort. The two sorting libraries are also independent from each other. With the re-built libraries, the test applications can be re-built in any order.
Each of the Visual Studio solutions listed in Figure 21 contains a _TXT sub-directory in which there are one or more text files describing the update history of the solution’s C# source file(s).
12. References
Dijkstra, E.W., 1981.
"Smoothsort, an alternative for sorting in situ." Article EWD796a, 16 August 1981. In the E.W.Dijkstra Archive, available from the Department of Computer Sciences of the University of Texas at Austin.
Dijkstra, E.W. and W.H.J. Feijen, 1988.
A Method of Programming. Addison-Wesley Publishing Co., Inc. Reading, Massachusetts. First English edition printed in 1988. Reprinted in 1989.
Orejel, J.L., 2003.
"Applied Algorithms and Data Structures." Unpublished textbook. Appendix VI Solutions to Chapter 6 Exercises VI.2.1, Section 6.4.1, pp. VI-8 - VI.9.
Schwarz, K., 2011.
"Smoothsort Demystified." Unpublished article. Posted at https://www.keithschwarz.com/smoothsort/.
van Gasteren, A.J.M, E.W. Dijkstra, and W.H.J Feijen, 1981.
"Heapsort." Article AvG8/EWD794/WF39, 22 June 1981. In the E.W.Dijkstra Archive, available from the Department of Computer Sciences of the University of Texas at Austin.
Williams, J,W.J., 1964.
"Algorithm 232 HEAPSORT." Communications of the ACM, Vol. 7, No. 6, June 1964, pp. 347-348. Reprinted in Collected Algorithms from ACM, Vol. II, Algorithms 221-492, Association for Computing Machinery, Inc., New York, 1980, p. 232-P 1-0.
13. Postscript

In the Spring semester of 1986-87, as a doctoral student, the author had the privilege of taking Professor Edsger Wybe Dijkstra’s course "Capita Selecta in Computing Science" (Selected Topics in Computing Science) in the Department of Computer Sciences of the University of Texas at Austin. (Yes, I took the gruelling but fascinating final oral exam, having to prove the famous Knaster-Tarski theorem, and passed the course with a grade of "A"). This article is respectfully dedicated to Edsger’s memory.
History
- 11th December, 2023: Initial version
