Beginning today, we are initiating a series of articles on data clustering, featuring a comparison of significant algorithms in the field (in particular K-Means and DBSCAN). Our goal is to blend theoretical concepts with practical implementation (in C#), offering clear illustrations of the associated challenges.
Introduction
Clustering is a technique in machine learning and data analysis that involves grouping similar data points together based on certain features or characteristics. The goal of clustering is to identify natural patterns or structures within a dataset, organizing it into subsets or clusters. Data points within the same cluster are expected to be more similar to each other than to those in other clusters.
In essence, clustering allows for the discovery of inherent structures or relationships in data, providing insights into its underlying organization. This technique is widely used in various fields, including pattern recognition, image analysis, customer segmentation, and anomaly detection. Common clustering algorithms include K-Means, hierarchical clustering, CURE and DBSCAN.
In this series of articles, we will implement the main clustering techniques in C# and endeavor to compare each one, assessing their strengths and weaknesses. This exploration will provide insights into the situations and types of data where each algorithm is better suited.
This article was originally posted here.
What is Clustering?
Clustering is a technique in machine learning and data analysis that involves grouping a set of data points into subsets or clusters based on their inherent similarities. The primary goal of clustering is to organize and uncover patterns within the data, allowing for the identification of meaningful structures or relationships.
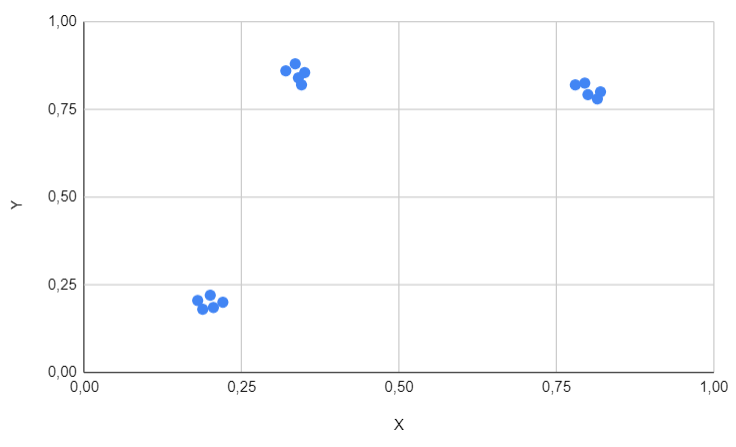
The process involves partitioning the data into groups in such a way that data points within the same cluster are more similar to each other than to those in other clusters. Similarity is typically measured using distance metrics, and various algorithms, such as K-Means, hierarchical clustering, and DBSCAN, are employed to perform clustering tasks. For example, it seems quite natural to identify three distinct clusters that are clearly separated in the figure above.
However, clustering can sometimes become more challenging, as illustrated in the example below, where the clusters exhibit more irregular shapes and are not easily separable by linear boundaries.

What Characteristics Should a Clustering Algorithm Possess?
The typical response is, as always: it varies. It genuinely depends on the specific application in question. In practical terms, certain algorithms excel in certain situations while performing inadequately in others. Some algorithms may demonstrate adaptability to challenging scenarios but come with a high computational cost. In this section, our aim is to highlight the characteristics that are frequently essential.
To ensure maximum conciseness, our study will focus exclusively on continuous input variables, considering only Euclidean spaces where distances and angles can be defined. This restriction is due to the fact that certain algorithms involve the computation of point averages, a task that is notably more straightforward in Euclidean spaces.
How Will We Compare Algorithms?
Our objective in this series is to assess various state-of-the-art algorithms, and we will achieve this by utilizing straightforward predefined datasets consisting of only two features, X and Y.
- The first dataset is the most basic and will allow us to observe how the algorithms perform in straightforward scenarios.

- The second dataset is nearly identical but incorporates two outliers, providing insight into algorithm behavior in the presence of outliers.

- Lastly, the third dataset explores algorithm performance when data is not linearly separable or exhibits irregular shapes.

The goal is to assess how each analyzed algorithm performs with these three datasets and determine the relevance of the resulting clusters. Specifically, we will delve into the following questions in great detail.
Is It Necessary to Predefine the Number of Clusters?
Determining the appropriate number of clusters has consistently posed a challenge, leading some algorithms, such as the well-established K-Means, to require this number as an input. This necessitates having a prior understanding of the potential number of groups within the dataset.
Important
It's important to note that this requirement is not necessarily a drawback, as specifying the number of clusters can align with specific business requirements.
On the contrary, other algorithms do not enforce a predetermined number of clusters; instead, they autonomously determine it as part of their inherent process.
What Does Sensitivity to Outliers Entail?
Outliers are data points that deviate significantly from the rest of the dataset, often lying at an unusual distance from the central tendency of the distribution. These data points are considered unusual or atypical compared to the majority of the other observations in the dataset. Outliers can influence statistical analyses and machine learning algorithms, potentially leading to skewed results or biased models. Identifying and handling outliers is crucial in data preprocessing to ensure the robustness and accuracy of analytical processes.

The two points highlighted in red are evidently anomalous, as they do not align with the other points.
The second dataset will enable us to observe how sensitive algorithms are to outliers.
What Occurs When the Data Exhibits Irregular Shapes?
The majority of algorithms operate effectively with linearly separable data, meaning data that can be divided by straight lines or planes. However, situations may arise where the data displays irregular or degenerate shapes, as illustrated in the figure below. In such cases, does the algorithm possess the capability to accurately cluster the dataset?

Is the Implementation of the Algorithm Straightforward, and Does It Demonstrate Efficiency?
Last but not least, it is crucial to assess whether the algorithm can be easily implemented and comprehended in a specific programming language. An algorithm that is overly intricate, requiring exceptional mathematical skills or proving challenging to articulate, might not find widespread utility.
Equally important is its efficiency. Once again, the question arises: how valuable is a highly efficient method capable of handling outliers or distinguishing irregular shapes if its computational complexity is exponential?
In this series, we will endeavor to scrutinize each of these characteristics for the algorithms under study. This approach will provide a clearer insight into the strengths and weaknesses of each algorithm.
Which Algorithms Are We Going to Analyze?
There exists a multitude of clustering algorithms and various versions of each. In this context, we will focus on three specifically: firstly, the widely utilized K-Means, followed by hierarchical methods, and finally, the often underestimated DBSCAN technique.
Before delving into the C# implementation of the three algorithms, we will briefly outline the logical structure of the Visual Studio project in this post.
As explained in the previous post, we will exclusively use a dataset with two features, X and Y. Consequently, we will have a very simple DataPoint class to model a record.
public class DataPoint : IEquatable<DataPoint>
{
public double X { get; set; }
public double Y { get; set; }
public double ComputeDistance(DataPoint other)
{
var X0 = other.X; var Y0 = other.Y;
return Math.Sqrt((X-X0)*(X-X0) + (Y-Y0) * (Y-Y0));
}
public bool Equals(DataPoint? other)
{
return other != null && X == other.X && Y == other.Y;
}
public override int GetHashCode()
{
return X.GetHashCode() ^ Y.GetHashCode();
}
}
Important
Note that we have implemented a ComputeDistance method to assess the similarity or dissimilarity between points. The chosen distance metric is the Euclidean one. In a real-world scenario, the distance should be provided as an argument in the constructor through dependency injection.
A dataset is simply a list of DataPoint objects.
public class Dataset
{
public List<DataPoint> Points { get; set; }
private Dataset() { Points = new List<DataPoint>(); }
public static Dataset Load(string path)
{
var set = new Dataset();
var contents = File.ReadAllLines(path);
foreach (var content in contents.Skip(1))
{
var d = content.Split(';');
var point = new DataPoint()
{ X = Convert.ToDouble(d[0]), Y = Convert.ToDouble(d[1]) };
set.Points.Add(point);
}
return set;
}
}
Important
Data is supplied through a file and loaded using the Load method.
As the goal is to define clusters, we need to model this entity in C#. Thus, a DataCluster is simply a list of DataPoint objects labeled with a cluster number.
public class DataCluster : IEquatable<DataCluster>
{
public List<DataPoint> Points { get; set; }
public string Cluster { get; set; }
public DataPoint GetCentroid()
{
var avgx = Points.Average(t => t.X);
var avgy = Points.Average(t => t.Y);
return new DataPoint() { X = avgx, Y = avgy };
}
public bool Equals(DataCluster? other)
{
return other != null && Cluster == other.Cluster;
}
public override int GetHashCode()
{
return Cluster.GetHashCode();
}
}
With this foundational code in place, it becomes possible to define an interface that all the algorithms will be required to implement.
public interface IClusteringStragtegy
{
List<DataCluster> Cluster(Dataset set, int clusters);
}
This interface contains only one method, the objective of which is to obtain the DataCluster objects from a dataset and a predefined number of clusters to discover.
To be comprehensive, the file containing the data resembles the following format for the first dataset presented earlier.
X;Y
0.2;0.22
0.22;0.2
0.18;0.205
0.188;0.18
0.205;0.185
0.8;0.792
0.82;0.8
0.78;0.82
0.795;0.825
0.815;0.78
0.34;0.84
0.32;0.86
0.335;0.88
0.345;0.82
0.35;0.855
We can now commence our exploration, starting with the venerable K-Means.
What is K-Means?
K-Means is a popular clustering algorithm used in machine learning and data analysis. It belongs to the category of partitioning methods and is designed to partition a dataset into a specific number of clusters (K), where each data point belongs to the cluster with the nearest mean. The algorithm iteratively refines its clusters by assigning data points to the cluster with the closest centroid and updating the centroids based on the mean of the assigned points.
The basic steps of the K-Means algorithm are thus as follows. Note that we have utilized images from Wikipedia.
- Initialize

We randomly select K data points from the dataset as initial cluster centroids.
- Assign

We assign each data point to the cluster whose centroid is the closest (usually based on Euclidean distance).
- Update

We recalculate the centroids of each cluster based on the mean of the data points assigned to that cluster.
- Repeat

We repeat the assignment and update steps until convergence, where the centroids no longer change significantly or a predefined number of iterations is reached.
Important 1
The centroid of a cluster is the arithmetic mean of all the data points in that cluster.
Important 2
The initialization of points in K-Means is not entirely random; rather, it aims to choose points in a way that is likely to distribute the KK points across different clusters. Various techniques exist for this purpose, but we won't delve into the details of these techniques here. Interested readers can refer to the implemented code.
Important 3
In real-world scenarios, it is common practice to normalize data before processing it.
Implementation in C#
As mentioned in the previous post, we need to implement the IClusteringStrategy interface.
public class KMeansClusteringStrategy : IClusteringStragtegy
{
public KMeansClusteringStrategy()
{
}
public List<DataCluster> Cluster(Dataset set, int clusters)
{
var groups = Initialize(set, clusters);
while (true)
{
var changed = false;
foreach (var point in set.Points)
{
var currentCluster = groups.FirstOrDefault
(t => t.Points.Any(x => x == point));
if (currentCluster == null) changed = true;
var d = double.MaxValue; DataCluster selectedCluster = null;
foreach (var group in groups)
{
var distance = point.ComputeDistance(group.GetCentroid());
if (d > distance)
{
selectedCluster = group;
d = distance;
}
}
if (selectedCluster != currentCluster)
{
selectedCluster?.Points.Add(point);
currentCluster?.Points.Remove(point);
changed = true;
}
}
if (!changed) break;
}
return groups;
}
#region Private Methods
private List<DataCluster> Initialize(Dataset set, int clusters)
{
var results = new List<DataCluster>();
var selectedPoints = new List<DataPoint>();
var r = new Random(); var k = r.Next(set.Points.Count);
var p = set.Points.ElementAt(k); selectedPoints.Add(p);
var c = 1;
var cluster = new DataCluster()
{ Cluster = c.ToString(), Points = new List<DataPoint>() { p } };
results.Add(cluster);
while (c < clusters)
{
var remainingPoints = set.Points.Except(selectedPoints).ToList();
var maximum = double.MinValue; DataPoint other = null;
foreach (var point in remainingPoints)
{
var distance = selectedPoints.Select(x => x.ComputeDistance(point)).Min();
if (distance > maximum)
{
maximum = distance;
other = point;
}
}
selectedPoints.Add(other);
c++;
var newCluster = new DataCluster()
{ Cluster = c.ToString(), Points = new List<DataPoint>() { other } };
results.Add(newCluster);
}
return results;
}
#endregion
}
K-Means is renowned for its simplicity, as evident in the preceding code with only a few lines. Undoubtedly, this simplicity contributes to its widespread use. On our part, we will explore how this algorithm performs on our three datasets.
Results for the First Dataset
Keep in mind that the first dataset is purely academic and serves as a straightforward test to ensure the algorithm functions on simple cases.

We can observe that, as expected, the clusters are perfectly identified and there is nothing additional to note regarding this specific case.
Results for the Second Dataset
The second dataset is employed to illustrate the impact of outliers.

This result prompts further commentary. Despite having only two outliers (albeit exaggerated), the algorithm appears to struggle. This underscores one of the key insights from this series: K-Means is highly sensitive to outliers, and a robust preprocessing step, specifically designed for outlier detection, should be implemented before applying this method indiscriminately.
Results for the Third Dataset
The third dataset is used to demonstrate how the algorithm performs in more challenging or pathological cases.
Caution
In this case, there are two clusters (not three, as before).

Once again, this result prompts further comments: K-Means struggles significantly with irregular shapes or data that is not linearly separable. This characteristic can pose a challenge. In our figure, it is relatively easy to discern that the data is pathological, but in real-world scenarios with very high dimensions, visualizing this fact becomes more challenging. We need to trust our understanding of the problem at hand to ensure that we can apply K-Means and obtain accurate results.
To Be Remembered
K-Means is easy to comprehend and implement, performing efficiently when dealing with simple and spherical clusters. However, it has limitations:
- It is highly sensitive to outliers.
- It requires a predefined number of clusters as input.
- It is not well-suited for datasets with irregular shapes.
Can we improve and address some of the limitations mentioned here? This is the topic of the next article dedicated to hierarchical clustering.
What is Hierarchical Clustering?
Hierarchical clustering is a clustering algorithm that creates a hierarchy of clusters. The algorithm iteratively merges or divides clusters based on the similarity or dissimilarity between them until a predefined stopping criterion is met.
There are two main types of hierarchical clustering: agglomerative or divisive.
-
Agglomerative hierarchical clustering starts with each data point as a separate cluster and successively merges the closest pairs of clusters until only one cluster remains. The merging process is often based on distance measures like Euclidean distance.
-
Divisive hierarchical clustering starts with all data points in a single cluster and recursively divides the cluster into smaller clusters until each data point is in its own cluster. Similar to agglomerative clustering, divisive clustering uses distance measures or linkage criteria for the splitting process.
Important
We will only implement an agglomerative hierarchical clustering in this post.
In theory, hierarchical clustering is advantageous in that it doesn't require specifying the number of clusters beforehand. However, it requires for that a stopping criterion that is not easy to determine organically. Therefore, in this post, we will predefine the number of clusters to be identified.
How to Implement Hierarchical Clustering?
Imagine a situation in which we need to cluster the following dataset.

We start with each point in its own cluster (in our case, we thus start with 11 clusters). Over time, larger clusters will be formed by merging two smaller clusters. But how do we decide which two clusters to merge ? We will delve into that in the next section, but for now, the algorithm can be described as follows:
WHILE we have the right number of clusters DO
pick the best two clusters to merge
combine those clusters into one cluster
END
How Do We Decide Which Two Clusters to Merge?
In fact, there are several rules for selecting the best clusters to merge. In this post, we will use the minimum of the distances between any two points, with one point chosen from each cluster. Other rules are possible; for example, we could identify the pair with the smallest distance between their centroids.
- According to our rule, the two closest clusters are 9 and 11, so we merge these two clusters.

- Now, we chose to cluster the point 8 with the previous cluster of two pints (9 and 11) since the point 8 and 9 are very close and no other pair of unclustered points is that close.

- Then, we chose to cluster the point 5 and 7.

- And so forth until we have reached the desired number of clusters.
Implementation in C#
We need to implement the IClusteringStrategy interface.
public class HierarchicalClusteringStrategy : IClusteringStragtegy
{
public List<DataCluster> Cluster(Dataset set, int clusters)
{
var results = new List<DataCluster>(); var c = 1;
foreach (var point in set.Points)
{
var cluster = new DataCluster()
{
Cluster = c.ToString(),
Points = new List<DataPoint> { point }
};
results.Add(cluster);
c++;
}
var currentNumber = results.Count;
while (currentNumber > clusters)
{
var minimum = double.MaxValue; var clustersToMerge = new List<DataCluster>();
foreach (var cluster in results)
{
var remainingClusters = results.Where(x => x != cluster).ToList();
foreach (var remainingCluster in remainingClusters)
{
var distance = ComputeDistanceBetweenClusters
(cluster, remainingCluster);
if (distance < minimum)
{
minimum = distance;
clustersToMerge = new List<DataCluster>()
{ cluster, remainingCluster };
}
}
}
var newCluster = new DataCluster()
{
Cluster = clustersToMerge.Select
(x => Convert.ToInt32(x.Cluster)).Min().ToString(),
Points = clustersToMerge.SelectMany(x => x.Points).ToList()
};
foreach (var delete in clustersToMerge)
results.Remove(delete);
results.Add(newCluster);
currentNumber = results.Count;
}
return results;
}
private double ComputeDistanceBetweenClusters
(DataCluster dataCluster1, DataCluster dataCluster2)
{
var minimum = double.MaxValue;
foreach (var point1 in dataCluster1.Points)
{
foreach (var point2 in dataCluster2.Points)
{
var distance = point1.ComputeDistance(point2);
if (distance < minimum)
{
minimum = distance;
}
}
}
return minimum;
}
}
Results for the First Dataset
Keep in mind that the first dataset is purely academic and serves as a straightforward test to ensure the algorithm functions on simple cases.

We can observe that, as expected, the clusters are perfectly identified and there is nothing additional to note regarding this specific case.
Results for the Second Dataset
The second dataset is employed to illustrate the impact of outliers.

Despite the existence of outliers, it is evident that hierarchical clustering responds appropriately and effectively identifies precise clusters. Consequently, hierarchical clustering demonstrates greater resilience to outliers compared to K-Means.
Results for the Third Dataset
The third dataset is used to demonstrate how the algorithm performs in more challenging or pathological cases.
Caution
In this case, there are two clusters (not three, as before).

Thus, hierarchical clustering appears to adeptly handle irregular shapes and is not impeded by data that is not linearly separable.
To Be Remembered
Hierarchical clustering is easy to comprehend and implement and is quite robust to outliers. Additionally, it seems well-suited for datasets with irregular shapes.
Moreover, hierarchical clustering is easy to understand and implement, and it is quite robust to outliers. Additionally, it appears well-suited for datasets with irregular shapes. Hierarchical clustering seems like a magical method, prompting the question of why it is not more widely used. However, a key point is not evident in the preceding examples: hierarchical clustering can be computationally intensive and less suitable for large datasets compared to methods like K-Means.
The algorithm for hierarchical clustering is not very efficient. At each step, we must compute the distance between each pair of clusters, in order to find the best merger. The initial step takes O(n2) time [nn is the number of records in the dataset], but the subsequent steps take time time proportional to (n−1)2, (n−2)2, ... The sum of squares up to nn is O(n3), so the algorithm is cubic. Thus, it cannot be run except for fairly small numbers of points.
Leskovec, Rajaraman, Ullman (Mining of Massive Datasets)
Even though more optimized versions of this algorithm exist (especially those incorporating priority queues), the execution time is still relatively high. As a result, this method can be employed only for small datasets.
Can we improve and address some of the limitations mentioned here? To avoid overloading this article, readers interested in the answer can find it here.
History
- 8th January, 2024: Initial version
