Fast Computation of PRNG's

Most PRNGs available deliver an unsigned integer of either 32-bit or 64-bit. We start by looking at what is available in the standard C++ random library. We discard most of them as insufficient by today's standards. Then, we look at newer versions like the Xoshiro family of PRNGs and Bernstein's Chacha20, whose quality is also sufficient for many cryptographic applications. Since the PRNGs in C++ are built as classes, we will build Xoshiro's and ChaCha20 using the same class structure. We finally look at the performance of these methods and provide a recommendation. All C++ code is adapted from various C sources and transform into the C++ class structure.

Contents

• Pseudorandom Number Generation (PRNG) Algorithm in the C++ standard library    
• The Mersenne Twister  
• Initializing the Mersenne Twister algorithm 
• The Xoshiro family of PRNG  
• Source code for Xoshiro256** class  
• The ChaCha family of PRNG  
• Initialization of the ChaCha20 PRNG involves three distinct keys:  
• Is ChaCha20 considered cryptographic-grade?  
• Source code for Chacha20 class  
• Performance  
• Recommendation  
• Reference   
• Appendix   
• Source code for other Xoshiro class's

Pseudorandom Number Generation (PRNG) Algorithm in the C++ standard library

In [2] & [3], there is an accessible introduction to the various Pseudorandom Number Generation (PRNG) algorithms available in the C++ standard library. Generally speaking, many PRNGs are not helpful in actual practice except maybe for the Mersenne twister PRNG. Below is the table showing the capability of the C++20 standard from [2].

As recommended in [2], the preferred choice for a pseudorandom number generator (PRNG) is the Mersenne Twister. However, other PRNGs that are not part of the standard C++ Library are also worth considering. In this section, we will discuss the implementation of the following PRNGs:

• Mersenne Twister
• Xoshiro family of scrambled linear PRNGs
• ChaCha family of cryptographic-strength PRNGs

Please note that PRNGs 1-2 are only recommended for non-cryptographic purposes. While there are C++ sources available for many of these PRNGs, they are typically designed to work with either 32-bit or 64-bit versions.
Most PRNGs in the C++ library are structured around classes, and we will adhere to this design approach by showing other PRNG algorithms. This allows us to utilize the same methods and design philosophy as the built-in versions, making it easier to transition from a built-in type to other types, as shown in the layout below. Generally, the following methods are available for most PRNGs:

• The class's constructor: This initializes the PRNG with either a default seed or a seed obtained from the seed_seq class.
• The () operator: This generates the following pseudorandom number.
• Member methods:
• a.    seed(): Allows manual seeding of the PRNG.
• b.    min(): Returns the minimum number that the PRNG can generate.
• c.    max(): Returns the maximum number that the PRNG can generate.
• d.   discard(): Discards a specified number of subsequent pseudorandom numbers.
• Non-member methods:
• a.    == relational operator
• b.    != relational operator

Sometimes, PRNGs require a warm-up period to improve the quality of the generated random numbers. This can be achieved by discarding a certain number of initial pseudorandom numbers using the discard() member function or utilizing the seed_seq class to provide better initial seeding.
It's important to note that all non-cryptographic PRNGs mentioned here are deterministic. This means if we seed the PRNG with the same value, it will produce the same sequence of numbers each time. Refer to [2] and [3] for a beginner-friendly introduction to PRNGs.
In the following sections, we will introduce each PRNG, providing a brief history and simplified explanations before delving into their arbitrary precision implementations.

The Mersenne Twister

The Mersenne Twister is a widely used pseudorandom number generator (PRNG) algorithm known for its long period and good statistical properties. It was developed by Makoto Matsumoto and Takuji Nishimura in 1997.
The Mersenne Twister is based on a large Mersenne prime number, a prime number in the form 2^p - 1, where p is also a prime number. The Mersenne Twister uses a 32-bit variant of the Mersenne Prime, specifically the Mersenne Prime with p = 19937.
There are four key features and properties of the Mersenne Twister:

1. Period: The Mersenne Twister has a period of 2¹⁹⁹³⁷ - 1, which means it can generate 2¹⁹⁹³⁷ - 1 distinct random number before repeating. This period is extensive, ensuring a vast number of unique random values.
2. Uniformity: The generated random numbers by the Mersenne Twister are uniformly distributed over the entire range of possible values. Each value has an equal chance of being generated.
3. Speed: The Mersenne Twister is known for its relatively fast generation speed. Although it is not the fastest PRNG available, it strikes a good balance between speed and quality of randomness.
4. State and Seeding: The Mersenne Twister has an internal state of 624 32-bit integers. The state determines the current position in the sequence of random numbers. By default, when you create an instance of the Mersenne Twister engine, it is seeded with a value obtained from the system clock. However, you can also manually seed it with a specific value.

However, The Mersenne Twister also has some weaknesses, such as its predictableness and failure of some statistical tests.
To use the Mersenne Twister PRNG in C++ with the standard library, you can instantiate the std::mt19937 or std::mt19937_64 classes from the <random> header, depending on whether you want a 32-bit or 64-bit variant. You can then generate random numbers by calling member functions operator().

Initializing the Mersenne Twister algorithm

The std::mt19937 class uses a 32-bit version of the Mersenne prime with p = 19937. The internal state of the Mersenne Twister consists of an array of 624 32-bit integers. These integers are collectively referred to as the "state vector."
A seed value is required to initialize the state vector of the Mersenne Twister. The seed value generates the initial state by applying the "twist" operation. The twist operation helps to ensure that the generated sequence of random numbers exhibits good statistical properties and has an extended period.
The seed value passed to the std::mt19937 constructor or the seed() function can be of various types, such as an integer or a sequence of integers. When you provide a single integer seed, the seed value is first used to initialize the first element of the state vector. Then, the subsequent elements of the state vector are filled based on a specific algorithm.
Here's a simplified explanation of the initialization process:

• The seed value is used as the first element of the state vector.
• A recurrence relation is applied to generate the remaining 623 elements of the state vector. The Mersenne Twister algorithm defines this recurrence relation and involves bitwise operations, shifts, and exclusive OR (XOR) operations.
• The twist operation is performed After filling the entire state vector. This operation mixes the state vector elements to enhance the randomness and improve statistical properties.
• The Mersenne Twister algorithm requires a warm-up phase to ensure the generated random numbers are not correlated with the initial seed. During this phase, a certain number of random numbers are generated and discarded before the generator is considered fully initialized.

Once the internal state is initialized, subsequent calls to generate random numbers will update and modify the state vector accordingly, producing a sequence of random numbers.
It's worth noting that the specific details of the initialization and the twist operation are more involved and rely on intricate mathematical properties of the Mersenne Twister algorithm. However, this simplified explanation provides a general understanding of how the state vector is initialized in the std::mt19937 class.
 

The Xoshiro family of PRNG

The Xoshiro family [7] of Scrambled linear pseudorandom number generators (PRNGs) is a renowned collection of algorithms designed to generate high-quality random numbers with exceptional statistical properties. Developed by Sebastiano Vigna, these PRNGs are widely recognized for their simplicity, speed, and remarkable period lengths.
The Xoshiro family comprises four distinct PRNGs: Xoshiro256**/Xoshiro256++, Xoshiro512**/Xoshiro512++, Xoshiro1024**/Xoshiro1024++, and Xoshiro128+. The nomenclature indicates the state size of each generator, where ++ is a strong summarization scrambler and ** indicates a strong multiplicative scrambler. 
Utilizing a combination of bitwise operations, shifts, and xor operations, these PRNGs excel in providing random numbers. They are specifically optimized for 64-bit systems, leveraging the inherent efficiency of native 64-bit arithmetic available on such platforms.
Here's a concise overview of the four members of the Xoshiro family:

1. Xoshiro256**/Xoshiro256++: This PRNG possesses a state size of 256 bits and executes 64 rounds. With a period length of 2²⁵⁶ - 1, it generates an extensive array of unique random values before repeating.
2. Xoshiro512**/Xoshiro512++: Featuring a state size of 512 bits and 64 rounds, Xoshiro512** offers an even lengthier period of 2⁵¹² - 1, ensuring an exceptionally vast sequence of random numbers.
3. Xoshiro1024**/Xoshiro1024++: With a state size of 1,024 bits and 64 rounds, Xoshiro1024** caters to applications requiring an extensive stream of random numbers. It boasts an impressive period length of 2¹⁰²⁴ - 1.
4. Xoshiro128+: As a smaller variant within the Xoshiro family, Xoshiro128+ possesses a state size of 128 bits and executes 24 rounds. Although it has a relatively shorter period of 2¹²⁸ - 1, it still delivers excellent random number generation capabilities, particularly for applications that do not require an exceedingly long period.

The Xoshiro family is a highly regarded choice due to its exceptional speed, statistical quality, and user-friendliness. These PRNGs find utility in various applications, including simulations, cryptography, gaming, and general-purpose random number generation.
It is crucial to acknowledge that while the Xoshiro PRNGs demonstrate remarkable efficiency and produce high-quality random numbers, they are unsuitable for cryptographic purposes that demand robust security measures.

Source code for Xoshiro256** class

// xoshiro256** random number generator implementation
/* This is xoshiro256** 1.0, one of our all-purpose generators. 
   It has excellent (sub-ns) speed, a state (256 bits) that is
   large enough for any parallel application, and it passes all tests we
   are aware of.

   For generating just floating-point numbers, xoshiro256+ is even faster.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest seeding a splitmix64 generator and using its
   output to fill s.
*/
class xoshiro256ss
{// Private
    using result_type = uint64_t;
    std::array<result_type,4> s;   // Internal state 256 bits

    static inline result_type rotl(const result_type x, const int k)
    {
        return (x << k) | (x >> (64 - k));
    }

    static inline result_type splitmix64(result_type x)
    {
        x += 0x9E3779B97F4A7C15;
        x = (x ^ (x >> 30)) * 0xBF58476D1CE4E5B9;
        x = (x ^ (x >> 27)) * 0x94D049BB133111EB;
        return x ^ (x >> 31);
    }

public:
    xoshiro256ss(const result_type val = std::random_device{}() )
    {// Initialization
        seed(val);
    }

    xoshiro256ss(const seed_seq& seeds)
    {   // Initialization through seed_seq seed
        seed(seeds);
    }

    void seed(const result_type seed_value)
    {
        for (int i = 0; i < 4; ++i)
            s[i] = splitmix64(seed_value + i);
    }

   void seed(const seed_seq& seeds)
    {   // Initialization through seed_seq seed
        std::array<unsigned, 4> sequence;
        seeds.generate(sequence.begin(), sequence.end());
        for (int i = 0; i < sequence.size(); ++i)
            s[i] = splitmix64(static_cast<result_type>(sequence[i]));
    }

    static result_type min()
    {
        return result_type(0ull);
    }

    static result_type max()
    {
        return  std::numeric_limits<result_type>::max();
    }
        
    result_type operator()() 
    {   // 256**
        const uint64_t result = rotl(s[1] * 5, 7) * 9;
        const uint64_t t = s[1] << 17;

        s[2] ^= s[0];
        s[3] ^= s[1];
        s[1] ^= s[2];
        s[0] ^= s[3];
        s[2] ^= t;
        s[3] = rotl(s[3], 45);

        return result;
    }

    bool operator==(const xoshiro256ss& rhs) const
    {
        return this->s == rhs.s;
    }

    bool operator!=(const xoshiro256ss& rhs) const
    {
        return this->s != rhs.s;
    }

    void discard(const unsigned long long z)
    {
        for (unsigned long long i = z; i > 0; --i)
            (void)this->operator()();
    }
};

The source for Xoshiro256++, Xoshiro512++, Xoshiro512** can be found in Appendix
 

The ChaCha family of PRNG.

The ChaCha family of pseudorandom number generators (PRNGs) encompasses a set of stream ciphers devised by Daniel J. Bernstein [5] & [6]. Initially developed for cryptographic purposes, the ChaCha algorithms have also proven valuable in generating random numbers for non-cryptographic applications.
The foundation of the ChaCha family lies in a construction known as a "quarter round" operation, which manipulates a 4x4 matrix of integers. The ChaCha algorithm generates pseudorandom numbers by repetitively applying this quarter-round operation in a specific pattern.
Various variants exist within the ChaCha family, including ChaCha8, ChaCha12, and ChaCha20, denoting the number of rounds executed during the quarter-round operation. Typically, a higher number of rounds enhances both the output's security and distribution quality, albeit at the cost of increased computational resources.
Each variant offers distinct trade-offs regarding security and performance, allowing users to select the most suitable one for their specific requirements. ChaCha20 has gained popularity due to its robust security properties and commendable performance.
The ChaCha algorithms are known for their simplicity, high-speed operation, and resilience against cryptographic attacks. They exhibit excellent statistical properties, featuring long periods and a uniform distribution of generated random numbers. Consequently, they are applicable across various domains, encompassing both cryptography and non-cryptographic fields.
Moreover, the ChaCha family extends its utility beyond PRNGs, encompassing symmetric encryption and authentication schemes.
The ChaCha family of PRNGs provides a dependable and efficient solution for generating pseudorandom numbers, with ChaCha20 standing out due to its strong security properties and widespread adoption.

Initialization of the ChaCha20 PRNG involves three distinct keys:

1. key
2. nonce
3. counter

When employing the ChaCha20 class, selecting appropriate values for the key, nonce, and counter is crucial to ensure the security and uniqueness of the generated pseudorandom numbers. Here are some recommendations:
The key should be a securely generated random sequence of bytes. It is vital to employ a solid and unpredictable key to maintain the security of the ChaCha20 cipher. The key's length should be 256 bits (32 bytes) for ChaCha20.
The nonce (number used once) should possess a unique value for each encryption session and must not be reused with the same key. For ChaCha20, the recommended nonce length is 96 bits (12 bytes). It can be generated randomly or incremented for each session.
The counter is an arbitrary value used to differentiate the generated blocks during the pseudorandom number generation process. Typically, it is initialized to 0 and incremented for each new block generated. If multiple instances of the ChaCha20 class are used concurrently, ensuring unique counters is crucial to avoid collisions.
Here's an example showcasing how to set the key, nonce, and counter when declaring the ChaCha20 class:

...
std::vector<uint8_t> key = { /* Your 32-byte key here */ };
std::vector<uint8_t> nonce = { /* Your 12-byte nonce here */ };
uint32_t counter = 0;
ChaCha20 prng(key, nonce, counter);
...

Use suitable random values for the key and nonce while ensuring the counter remains unique for each PRNG instance or session.
Furthermore, if ChaCha20 is employed for cryptographic purposes, adhering to best practices and security guidelines is essential. This encompasses proper key management, nonce handling, and overall system security.

Is ChaCha20 considered cryptographic-grade?

ChaCha20 is widely regarded as suitable for cryptographic applications. It is a widely employed stream cipher and has been adopted as one of the standard algorithms in various cryptographic protocols and systems.
ChaCha20 offers several advantages that make it well-suited for cryptographic usage:

• Extensive security analysis has confirmed ChaCha20's resilience against known cryptographic attacks. It ensures a high level of confidentiality when deployed as a symmetric encryption algorithm.
• ChaCha20 emphasizes speed and efficiency, resulting in highly efficient software implementations. This makes it a preferred choice for resource-constrained devices or applications where performance is critical.
• ChaCha20 incorporates a series of operations, including the quarter round and mixing operations, to achieve strong non-linearity and diffusion properties. These properties ensure that modifications in the input significantly impact the output, bolstering its resistance to cryptographic attacks.
• ChaCha20 supports key sizes of 128 bits and 256 bits, offering flexibility in selecting the appropriate key length based on the desired security level. Additionally, it employs a 96-bit nonce, enabling the generation of many unique streams.
• ChaCha20 enjoys widespread support in cryptographic libraries and protocols, including TLS/SSL, IPsec, and secure messaging applications.

The ChaCha20 is a secure and efficient choice for numerous cryptographic applications, including symmetric encryption, authenticated encryption, and secure communication protocols. However, it is crucial to follow recommended practices, ensuring proper implementation within the context of the specific cryptographic system or protocol being utilized.

Source code for Chacha20 class

// ChaCha20 PRNG class
class chacha20
{
    // ChaCh20 output 32-bit unsigned integers
    // The three initialization keys, nonce & counter
    std::vector<uint8_t> key_;     
    std::vector<uint8_t> nonce_;
    uint32_t counter_;          // Number of 16 block generated
    std::array<uint32_t, 16> block_; // Holds the next 16 random numbers
    int position_;              // Current position into the block generated

    // ChaCha20 constants
    const std::array<uint32_t, 4> kInitialState = { 0x61707865, 0x3320646e, 0x79622d32, 0x6b206574 };
    const std::array<uint8_t, 16> kSigma = { 'e', 'x', 'p', 'a', 'n', 'd', ' ', '3', '2', '-', 'b', 'y', 't', 'e', ' ', 'k' };

    // ChaCha20 quarter round operation
    static inline void QuarterRound(uint32_t& a, uint32_t& b, uint32_t& c, uint32_t& d)
    {
        a += b; d ^= a; d = (d << 16) | (d >> 16);
        c += d; b ^= c; b = (b << 12) | (b >> 20);
        a += b; d ^= a; d = (d << 8) | (d >> 24);
        c += d; b ^= c; b = (b << 7) | (b >> 25);
    }

    // ChaCha20 core function
    static void ChaCha20Core(const std::array<uint32_t, 16>& input, std::array<uint32_t, 16>& output)
    {
        std::array<uint32_t, 16> state = input;

        for (int i = 0; i < 10; ++i) {
            // Column rounds
            QuarterRound(state[0], state[4], state[8], state[12]);
            QuarterRound(state[1], state[5], state[9], state[13]);
            QuarterRound(state[2], state[6], state[10], state[14]);
            QuarterRound(state[3], state[7], state[11], state[15]);

            // Diagonal rounds
            QuarterRound(state[0], state[5], state[10], state[15]);
            QuarterRound(state[1], state[6], state[11], state[12]);
            QuarterRound(state[2], state[7], state[8], state[13]);
            QuarterRound(state[3], state[4], state[9], state[14]);
        }

        for (int i = 0; i < 16; ++i) {
            output[i] = state[i] + input[i];
        }
    }

    // Generate the next 16 random numbers
    void generateNewBlock()
    {
        std::array<uint32_t, 16> input;
        std::array<uint32_t, 16> output;

        // Set the ChaCha20 initial state
        input[0] = kInitialState[0];
        input[1] = kInitialState[1];
        input[2] = kInitialState[2];
        input[3] = kInitialState[3];

        // Set the key, nonce, and counter
        std::copy(kSigma.begin(), kSigma.end(), reinterpret_cast<uint8_t*>(&input[4]));
        std::copy(key_.begin(), key_.end(), reinterpret_cast<uint8_t*>(&input[8]));
        std::copy(nonce_.begin(), nonce_.end(), reinterpret_cast<uint8_t*>(&input[12]));
        input[14] = counter_;

        ChaCha20Core(input, output);

        // Copy the output to the block
        std::copy(output.begin(), output.end(), block_.begin());
        ++counter_;
    }

public:
    // Constructor
    chacha20(const std::vector<uint8_t>& key, const std::vector<uint8_t>& nonce, uint32_t counter)
        : key_(key), nonce_(nonce), counter_(counter), position_(0) {}
    chacha20()
    {
        seed();
    }

    // Seed
    void seed(const std::vector<uint8_t>& key, const std::vector<uint8_t>& nonce, uint32_t counter)
    {
        key_ = key;
        nonce_ = nonce;
        counter_ = counter;
        position_ = 0;
    }

    //seed with value
    void seed(const uint32_t s= std::random_device{}())
    {
        mt19937 gen(s);  // use the build in mt19937 PRNG for random values
        uniform_int_distribution<uint32_t> dis(1, 0xfe);

        key_.clear();
        for (int i = 0; i < 16; ++i)
            key_.push_back(static_cast<uint8_t>(dis(gen)));
        nonce_.clear();
        for (int i = 0; i < 8; ++i)
            nonce_.push_back(static_cast<uint8_t>(dis(gen)));
        counter_ = gen();
        position_ = 0;
    }

    void seed(const std::seed_seq& seeds)
    {// Initialization through seed_seq seed
        std::array<uint32_t, 16> sequencekey;
        std::array<uint32_t, 16> sequencenonce;
        std::array<uint32_t, 1> sequencecounter;  

        seeds.generate(sequencekey.begin(), sequencekey.end());
        key_.clear();
        for (int i = 0; i < 16; ++i)
            key_.push_back(static_cast<uint8_t>(sequencekey[i]));
        seeds.generate(sequencenonce.begin(), sequencenonce.end());
        nonce_.clear();
        for (int i = 0; i < 8; ++i)
            nonce_.push_back(static_cast<uint8_t>(sequencenonce[i]));

        seeds.generate(sequencecounter.begin(), sequencecounter.end());
        counter_ = sequencecounter[0];
        position_ = 0;
    }

    uint32_t operator()()
    {
        if (position_ == 0 || position_ >= 16)
        {
            generateNewBlock();
            position_ = 0;
        }

       uint32_t randomNumber = block_[position_];
        ++position_;
        return randomNumber;
    }

    static constexpr uint32_t min()
    {
        return uint32_t(0ul);
    }

    static constexpr uint32_t max()
    {
        return std::numeric_limits<uint32_t>::max();
    }

    bool operator==(const chacha20& rhs) const
    {
        return this->key_ == rhs.key_ && this->nonce_ == rhs.nonce_ && this->counter_ == rhs.counter_;
    }

    bool operator!=(const chacha20& rhs) const
    {
        return this->key_ != rhs.key_ || this->nonce_ != rhs.nonce_ || this->counter_ != rhs.counter_;
    }

    void discard(const unsigned long z)
    {
        for (unsigned long long i = z; i > 0; --i)
            (void)this->operator()();
    }
};

Performance

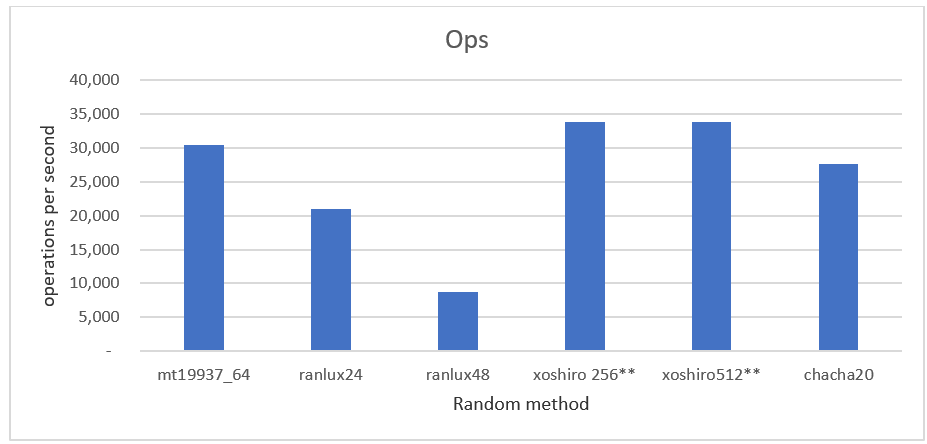
I was testing the performance of the various random methods. I noticed that ranlux24 and ranlux48 are considerably slower than the other methods. Both Xoshiro methods are slightly faster than mt19937, and ChaCha20 is trailing the mt199937 only by a small amount. If speed is of the essence, then I recommend the Xoshiro256 and Xoshiro512 methods. If you favor the cryptographic graded method, then I recommend the ChaCha20. Although ranlux48 is a high-quality PRNG, it is far behind the other methods in terms of speed. Generally, I agreed with [2] & [3] that there is no need to consider ranlux24 or ranlux48 unless you don't have an implementation of the Xoshiro or ChaCha20 

Recommendation

For a final recommendation, I recommend one of the Xoshiro family if speed is of the essence and the ChaCha20 if cryptographic grade quality is needed.

Reference

1. Arbitrary precision library package. Arbitrary Precision C++ Packages
2. Learn cpp chapter 7.19. 7.19 — Introduction to random number generation – Learn C++ (learncpp.com)
3. Learn cpp chapter 7.20.  7.20 — Generating random numbers using Mersenne Twister – Learn C++ (learncpp.com)
4. ChatGPT (www.openai.com)  on March 5, 2023
5. D.J. Bernstein. ChaCha. The ChaCha family of stream ciphers (yp.to)
6. D.J. Bernstein. ChaCha is a variant of Salsa. chacha-20080128.pdf (yp.to)
7. Xoshiro family of PRNGs. https://prng.di.unimi.it/

Appendix

Source Xoshiro Class

Source for Xoshiro256++ class

// xoshiro256++ random number generator implementation
/* This is xoshiro256++ 1.0, one of our all-purpose generators.
   It has excellent (sub-ns) speed, a state (256 bits) that is large
   enough for any parallel application, and it passes all tests we are
   aware of.

   For generating just floating-point numbers, xoshiro256+ is even faster.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest seeding a splitmix64 generator and using its
   output to fill s. */
class xoshiro256pp {
    using result_type = uint64_t;
    std::array<result_type, 4> s;   // Internal state 256 bits

    static inline result_type rotl(const result_type x, const int k)
    {
        return (x << k) | (x >> (64 - k));
    }

    static inline result_type splitmix64(result_type x) 
    {
        x += 0x9E3779B97F4A7C15;
        x = (x ^ (x >> 30)) * 0xBF58476D1CE4E5B9;
        x = (x ^ (x >> 27)) * 0x94D049BB133111EB;
        return x ^ (x >> 31);
    }

public:
    xoshiro256pp(const result_type val = std::random_device{}() /* 5489u*/)
    {// Initialization
        seed(val);
    }

    xoshiro256pp(const seed_seq& seeds)
    {   // Initialization through seed_seq seed
        seed(seeds);
    }

    void seed(const result_type seed_value) 
    { 
        for (int i = 0; i < 4; ++i) 
            s[i] = splitmix64(seed_value + i);
    }

   void seed(const seed_seq& seeds)
    {   // Initialization through seed_seq seed
        std::array<unsigned, 4> sequence;
        seeds.generate(sequence.begin(), sequence.end());
        for (int i = 0; i < 4; ++i)
            s[i] = splitmix64(static_cast<result_type>(sequence[i]));
    }

    static result_type min()
    {
        return result_type(0u);
    }

    static result_type max()
    {
        return  std::numeric_limits<result_type>::max();
    }

    result_type operator()() 
    {  /// 256++
        const result_type result = rotl(s[0] + s[3], 23) + s[0];
        const result_type t = s[1] << 17;

        s[2] ^= s[0];
        s[3] ^= s[1];
        s[1] ^= s[2];
        s[0] ^= s[3];
        s[2] ^= t;
        s[3] = rotl(s[3], 45);

        return result;
    }

    bool operator==( const xoshiro256pp& rhs) const
    {
        return this->s==rhs.s;
    }

    bool operator!=(const xoshiro256pp& rhs) const
    {
        return this->s != rhs.s;
    }

    void discard(const unsigned long long z)
    {
        for (unsigned long long i = z; i > 0; --i)
            (void)this->operator()();
    }
};

Source for Xoshiro512++ class

// xoshiro512++ random number generator implementation
/* This is xoshiro512++ 1.0, one of our all-purpose, generators. 
   It has excellent (about 1ns) speed, a state (512 bits) that
   is large enough for any parallel application, and it passes all tests
   we are aware of.

   For generating just floating-point numbers, xoshiro512+ is even faster.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest seeding a splitmix64 generator and using its
   output to fill s.
   */
class xoshiro512pp {   
    using result_type = uint64_t;
    std::array<result_type,8> s;   // Internal state 512 bits

    static inline result_type rotl(const result_type x, const int k) {
        return (x << k) | (x >> (64 - k));
    }

    static inline result_type splitmix64(result_type x) {
        x += 0x9E3779B97F4A7C15;
        x = (x ^ (x >> 30)) * 0xBF58476D1CE4E5B9;
        x = (x ^ (x >> 27)) * 0x94D049BB133111EB;
        return x ^ (x >> 31);
    }

public:
    xoshiro512pp(const result_type val = std::random_device{}() /*5489u*/)
    {// Initialization
        seed(val);
    }

    xoshiro512pp(const seed_seq& seeds)
    {   // Initialization through seed_seq seed
        seed(seeds);
    }

    void seed(const result_type seed_value) {
        for (int i = 0; i < 8; ++i) {
            s[i] = splitmix64(seed_value + i);
        }
    }

    void seed(const seed_seq& seeds)
    {   // Initialization through seed_seq seed
        std::array<unsigned, 8> sequence;
        seeds.generate(sequence.begin(), sequence.end());
        for (size_t i = 0; i < sequence.size(); ++i)
            s[i] = splitmix64(static_cast<result_type>(sequence[i]));
    }

    static result_type min()
    {
        return result_type(0ull);
    }

    static result_type max()
    {
        return  std::numeric_limits<result_type>::max();
    }

    result_type operator()()
    {//512++
        const result_type result = rotl(s[0] + s[2], 17) + s[2];
        const result_type t = s[1] << 11;

        s[2] ^= s[0];
        s[5] ^= s[1];
        s[1] ^= s[2];
        s[7] ^= s[3];
        s[3] ^= s[4];
        s[4] ^= s[5];
        s[0] ^= s[6];
        s[6] ^= s[7];
        s[6] ^= t;
        s[7] = rotl(s[7], 21);

        return result;
    }

    bool operator==(const xoshiro512pp& rhs) const
    {
        return this->s == rhs.s;
    }

    bool operator!=(const xoshiro512pp& rhs) const
    {
        return this->s != rhs.s;
    }

    void discard(const unsigned long long z)
    {
        for (unsigned long long i = z; i > 0; --i)
            (void)this->operator()();
    }
};

Source code for Xoshiro512** class

/* This is xoshiro512** 1.0, one of our all-purpose, generators
   with increased state size. It has excellent (about 1ns) speed, a state
   (512 bits) that is large enough for any parallel application, and it
   passes all tests we are aware of.

   For generating just floating-point numbers, xoshiro512+ is even faster.

   The state must be seeded so that it is not everywhere zero. If you have
   a 64-bit seed, we suggest seeding a splitmix64 generator and using its
   output to fill s.
   */
class xoshiro512ss {
    using result_type = uint64_t;
    std::array<result_type,8> s;       // Internal state 512 bits

    static inline result_type rotl(const result_type x, const int k) {
        return (x << k) | (x >> (64 - k));
    }

    static inline result_type splitmix64(result_type x) {
        x += 0x9E3779B97F4A7C15;
        x = (x ^ (x >> 30)) * 0xBF58476D1CE4E5B9;
        x = (x ^ (x >> 27)) * 0x94D049BB133111EB;
        return x ^ (x >> 31);
    }

public:
    xoshiro512ss(const result_type val = std::random_device{}())
    {   // Initialization
        seed(val);
    }

    xoshiro512ss(const seed_seq& seeds)
    {   // Initialization through seed_seq seed
        seed(seeds);
    }

    void seed(const result_type seed_value)
    {   // Regular seed
        for (int i = 0; i < 8; ++i) {
            s[i] = splitmix64(seed_value + i);
        }
    }

    void seed(const seed_seq& seeds)
    {   // Initialization through seed_seq seed
        std::array<unsigned, 8> sequence;
        seeds.generate(sequence.begin(), sequence.end());
        for (int i = 0; i < sequence.size(); ++i)
            s[i] = splitmix64(static_cast<result_type>(sequence[i]));
    }

    static result_type min()
    {
        return result_type(0ull);
    }

    static result_type max()
    {
       return std::numeric_limits<result_type>::max();
    }

    result_type operator()()
    {//512**
        const result_type result = rotl(s[1] * 5, 7) * 9;
        const result_type t = s[1] << 11;

        s[2] ^= s[0];
        s[5] ^= s[1];
        s[1] ^= s[2];
        s[7] ^= s[3];
        s[3] ^= s[4];
        s[4] ^= s[5];
        s[0] ^= s[6];
        s[6] ^= s[7];
        s[6] ^= t;
        s[7] = rotl(s[7], 21);

        return result;
    }

    bool operator==( const xoshiro512ss& rhs) const
    {
        return this->s == rhs.s;
    }

    bool operator!=(const xoshiro512ss& rhs) const
    {
        return this->s != rhs.s;
    }

    void discard(const unsigned long long z)
    {
        for (unsigned long long i = z; i > 0; --i)
            (void)this->operator()();
    }
};