Some Facts about OpenMP
This article is not a substitute for the documentation contained within the www.openmp.org web site. This site provides full documentation for the current version of the OpenMP API. In parallel computing, the strongest use of implicit threading is a specification called OpenMP. While considered to be an implicit threading library, OpenMP, or Open Multi-Processing, is an Application Program Interface (API) that may be used to explicitly direct multi-threaded, shared memory parallelism. OpenMP is not guaranteed to make the most efficient use of shared memory, so it is not meant for distributed memory parallel systems itself. OpenMP implements concurrency through special pragmas and directives inserted into your source code to indicate segments that are to be executed concurrently. These pragmas are recognized and processed by the compiler. This means that OpenMP capitalizes from the multi-core processor architecture. In short, it is vital to understand OpenMP in order to use these new multi-core processor architectures effectively.
Implicit threading libraries take care of much of the intricacies needed to create, manage, and (to some extent) synchronize threads. OpenMP is intended to be suitable for implementation on a broad range of SMP architectures, but it is not a new programming language. Rather, it is notations that can be added to a sequential program in FORTRAN, C, or C++ to describe how the work is to be shared among threads that will execute on different processors or cores and to order accesses to shared data as needed. The appropriate insertion of OpenMP features into a sequential program will allow many, perhaps most, applications to benefit from shared-memory parallel architectures, often with minimal modification to the code. In practice, many applications have considerable parallelism that can be exploited.
The success of OpenMP can be attributed to a number of factors. One is its strong emphasis on structured parallel programming. Another is that OpenMP is comparatively simple to use, since the burden of working out the details of the parallel program is up to the compiler. It has the major advantage of being widely adopted, so that an OpenMP application will run on many different platforms. But above all, OpenMP is timely. With the strong growth in deployment of both small and large SMPs and other multithreading hardware, the need for a shared-memory programming standard that is easy to learn and apply is accepted in the computing industry. This, in turn, means that all the major compilers--the Microsoft Visual C/C++ .NET for Windows and the GNU GCC compiler for Linux, and the Intel C/C++ compilers, for both Windows and Linux, also support OpenMP.
Some Basics about How OpenMP works
OpenMP directives demarcate code that can be executed in parallel (called parallel regions) and control how code is assigned to threads. The threads in an OpenMP code operate under the fork-join model. When the main thread encounters a parallel region while executing the application, a team of threads is forked off, and these threads begin executing the code within the parallel region. At the end of the parallel region, the threads within the team wait until all the other threads in the team have finished before being 'joined'. The main thread resumes serial execution with the statement following the parallel region. The implicit barrier at the end of all parallel regions (and most other constructs defined by OpenMP) preserves sequential consistency.
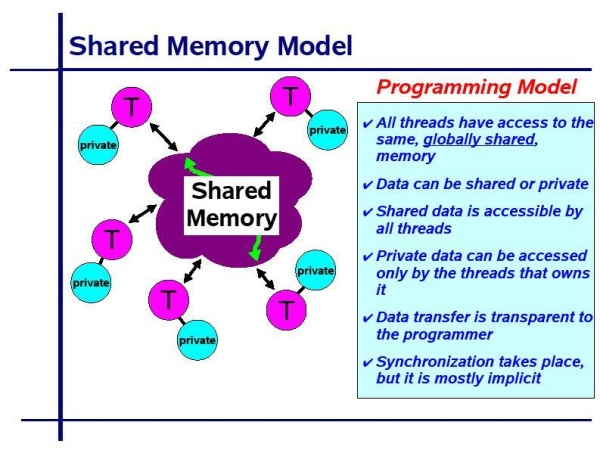
OpenMP's directives let the user tell the compiler which instructions to execute in parallel and how to distribute them among the threads that will run the code. An OpenMP directive is an instruction in a special format that is understood by OpenMP compilers only. In fact, it looks like a comment to a regular FORTRAN compiler or a pragma to a C/C++ compiler, so that the program may run just as it did beforehand if a compiler is not OpenMP-aware. The API does not have many different directives, but they are powerful when used effectively. So, stated crudely, OpenMP realizes a shared-memory (or shared address space) programming model. This model assumes, as its name implies, that programs will be executed on one or more processors that share some or all of the available memory. Shared-memory programs are typically executed by multiple independent threads (execution states that are able to process an instruction stream); the threads share data, but may also have some additional, private data.
Shared-memory approaches to parallel programming must provide, in addition to a normal range of instructions, a means for starting up threads, assigning work to them, and coordinating their accesses to shared data, including ensuring that certain operations are performed by one thread at a time. To reiterate, OpenMP implements concurrency through special pragmas and directives inserted into your source code to indicate segments that are to be executed concurrently. These pragmas are recognized and processed by the compiler. This pragma will be followed by a single statement or block of code enclosed with curly braces. When the application encounters this statement during execution, it will fork a team of threads, execute all of the statements within the parallel region on each thread, and join the threads after the last statement in the region.
In many applications, a large number of independent operations are found in loops. Using the loop worksharing construct in OpenMP, you can split up these loop iterations and assign them to threads for concurrent execution. The parallel for construct will initiate a new parallel region around the single for loop following the pragma, and divide the loop iterations among the threads of the team. Upon completion of the assigned iterations, threads sit at the implicit barrier at the end of the parallel region, waiting to join with the other threads. It is possible to split up the combined parallel for construct into two pragmas: a parallel construct and the for construct, which must be lexically contained within a parallel region. Use this separation when there is parallel work for the thread team other than the iterations of the loop. You can also attach a schedule clause to the loop worksharing construct to control how iterations are assigned to threads. The static schedule will divide iterations into blocks and distribute the blocks among threads before the loop iterations begin execution; round robin scheduling is used if there are more blocks than threads. The dynamic schedule will assign one block of iteration per thread in the team; as threads finish the previous set of iterations, a new block is assigned until all the blocks have been distributed. There is an optional chunk argument for both static and dynamic scheduling that controls the number of iterations per block. So, let's take a look at an example:
#include <stdio.h>
#include <stdlib.h>
int main(argc,argv)
int argc; char *argv[];
{
double sum;
double a [256], b [256];
int status;
int n=256;
int i;
for ( i = 0; i < n; i++) {
a [i] = i * 0.5;
b [i] = i * 2.0;
}
sum = 0;
#pragma omp parallel for reduction(+:sum)
for (i = 1; i <= n; i++ ) {
sum = sum + a[i]*b[i];
}
printf ("sum = %f \n", sum);
}
Compile: C:\..\..\>cl dot.c
Output
sum = 5559680.000000
Under OpenMP, all data is shared by default. In this case, we are able to parallelize the loop simply by inserting a directive that tells the compiler to parallelize it, and identifying sum as a reduction variable. The details of assigning loop iterations to threads, having the different threads build partial sums, and their accumulation into a global sum are left to the compiler. To repeat, by default, almost all variables in an OpenMP threaded program are shared between threads. The exceptions to this shared access rule are: the loop index variable associated with a loop worksharing construct (each thread must have its own copy in order to correctly iterate through the assigned set of iterations), variables declared within a parallel region or declared within a function that is called from within a parallel region, and any other variable that is placed on the thread's stack (e.g., function parameters). If you use nested loops within a loop worksharing construct in C/C++, only the loop index variable immediately succeeding the construct will automatically be made private. If other variables must be local to threads, such as the loop index variables for nested loops, add a private clause to the relevant construct. A local copy of the variables in the list will be allocated for each thread. The initial value of variables that are listed within the private clause will be undefined, and you must assign value to them before they are read within the region of use.
OpenMP has synchronization constructs that ensure mutual exclusion to your critical regions. Use these when variables must remain shared by all threads, but updates must be performed on those variables in parallel regions. The critical construct acts like a lock around a critical region. Only one thread may execute within a protected critical region at a time. Other threads wishing to have access to the critical region must wait until no thread is executing the critical region. Now, because we said that by default almost all variables in an OpenMP threaded program are shared between threads (that is, there is data passed between the threads), we can recall the exception to this rule and put it to use, that this shared access rule has an exception: the loop index variable associated with a loop worksharing construct.
This code is an example of Loop-Work sharing. In this example, the iterations of a loop are scheduled dynamically across the team of threads. A thread will perform CHUNK iterations at a time before being scheduled for the next CHUNK of work:
#include <omp.h>
#include <sdio.h>
#include <stdlib.h>
#define CHUNKSIZE 10
#define N 100
int main (int argc, char *argv[])
{
int nthreads, tid, i, chunk;
float a[N], b[N], c[N];
for (i=0; i < N; i++)
a[i] = b[i] = i * 1.0;
chunk = CHUNKSIZE;
#pragma omp parallel shared(a,b,c,nthreads,chunk) private(i,tid)
{
tid = omp_get_thread_num();
if (tid == 0)
{
nthreads = omp_get_num_threads();
printf("Number of threads = %d\n", nthreads);
}
printf("Thread %d starting...\n",tid);
#pragma omp for schedule(dynamic,chunk)
for (i=0; i<n; c[%d]="%f\n",tid,i,c[i]);")
c[i]="a[i]";
Output
Number of threads = 1
Thread 0 starting...
Thread 0: c[0]= 0.000000
Thread 0: c[1]= 2.000000
Thread 0: c[2]= 4.000000
Thread 0: c[3]= 6.000000
Thread 0: c[4]= 8.000000
Thread 0: c[5]= 10.000000
Thread 0: c[6]= 12.000000
Thread 0: c[7]= 14.000000
Thread 0: c[8]= 16.000000
Thread 0: c[9]= 18.000000
Thread 0: c[10]= 20.000000
Thread 0: c[11]= 22.000000
Thread 0: c[12]= 24.000000
Thread 0: c[13]= 26.000000
Thread 0: c[14]= 28.000000
Thread 0: c[15]= 30.000000
Thread 0: c[16]= 32.000000
Thread 0: c[17]= 34.000000
Thread 0: c[18]= 36.000000
Thread 0: c[19]= 38.000000
Thread 0: c[20]= 40.000000
. . . stopped here for brevity's sake..
This next example involves combined parallel loop reduction. It demonstrates a sum reduction within a combined parallel loop construct. Notice that default data element scoping is assumed. There are no clauses specifying shared or private variables. OpenMP will automatically make loop index variables private within team:
#include <omp.h>
#include <stdio.h>
#include <stdlib.h>
int main (int argc, char *argv[])
{
int i, n;
float a[100], b[100], sum;
n = 100;
for (i=0; i < n; i++)
a[i] = b[i] = i * 1.0;
sum = 0.0;
#pragma omp parallel for reduction(+:sum)
for (i=0; i < n; i++)
sum = sum + (a[i] * b[i]);
printf(" Sum = %f\n",sum);
}
Output
Sum = 328350.000000
A common computation is to summarize or reduce a large collection of data to a single value. For example, this may include the sum of the data items or the maximum or minimum of the data set. The algorithm to do such computations has a dependence on the shared variable used to collect the partial and final answers. OpenMP provides a clause to handle the details of a concurrent reduction. The reduction clause requires associative and commutative operations for combining data, as well as a list of reduction variables. Each thread within the parallel team will receive a private copy of the reduction variables to use when executing the assigned computations. Unlike variables contained in a private clause, these private variables are initialized with a value that depends on the reduction operation. At the end of the region with a reduction clause, all local copies are combined using the operation noted in the clause, and the result is stored in the shared copy of the variable. So at this point, let's a look at a numerical computation program, to then look at a threaded parallelized second version.
In Calculus, when we want to compute the area underneath a curve, we draw rectangles that approach the curvilinear line. The curve is continuous, meaning that it has a tangent line at every point. That is, at every single point that comprises the curve, there is a change, a change in direction. This is also called a differential coefficient. Each rectangle has a mid-point, and the rectangle has a height and a width. The narrower the rectangles, the more of them there are to sum. This is called nearing the area. Actually, Numerical Integration is a method of computing an approximation of the area under the curve of a function, especially when the exact integral cannot be solved. For example, the value of the constant Pi can be defined by the following integral. However, rather than solve this integral exactly, we can approximate the solution by the use of numerical integration:

The code in the example shown below is an implementation of the numerical integration midpoint rectangle rule to solve the integral just shown. To compute an approximation of the area under the curve, we must compute the area of some number of rectangles (num_rects) by finding the midpoint (mid) of each rectangle and computing the height of that rectangle (height), which is simply the function value at that midpoint. We add together the heights of all the rectangles (sum) and, once computed, we multiply the sum of the heights by the width of the rectangles (width) to determine the desired approximation of the total area (area) and the value of Pi. This is not a threaded application, but is code to show how it can be threaded when we write the second example:
#include <stdio.h>
static long num_rects=100000;
void main()
{
int i;
double mid, height, width, sum = 0.0;
double area;
width = 1.0/(double) num_rects;
for (i = 0; i < num_rects; i++){
mid = (i + 0.5) * width;
height = 4.0/(1.0 + mid*mid);
sum += height;
}
area = width * sum;
printf("Computed pi = %f\n",area);
}
Computed pi = 3.141593
The second application computes an approximation of the value for Pi using numerical integration and the midpoint rectangle rule, as in the first example. The code divides the integration range into num_rect intervals, and computes the functional value of 4.0/(1+x 2) for the midpoint of each interval (rectangle). In other words, the first step in creating an OpenMP program from a sequential one is to identify the parallelism it contains. Basically, this means finding instructions, sequences of instructions, or even large regions of code that may be executed concurrently by different processors:
#include <stdio.h>
#include <stdlib.h>
static long num_rects = 1000000;
int main(int argc, char* argv[])
{
double mid, height, width, sum=0.0;
int i;
double area;
width = 1./(double)num_rects;
#pragma omp parallel for private(mid, height) reduction(+:sum)
for (i=0; i < num_rects; i++) {
mid = (i + 0.5)*width;
height = 4.0/(1.+ mid*mid);
sum += height;
}
area = width * sum;
printf("The value of PI is %f\n",area);
}
The value of Pi is 3.141593.
An OpenMP loop worksharing construct has been added. The OpenMP-compliant compiler will insert code to spawn a team of threads, give a private copy of the mid, height, and i variables to each thread, divide up the iterations of the loop between the threads, and finally, when the threads are done with the assigned computations, combine the values stored in the local copies of sum into the shared version. This shared copy of sum will be used to compute the Pi approximation when multiplied by the width of the intervals.
Finally, let's examine a matrix multiplication code:
#include <omp.h>
#include <stdio.h>
#include <stdlib.h>
#define NRA 62 /* number of rows in matrix A */
#define NCA 15 /* number of columns in matrix A */
#define NCB 7 /* number of columns in matrix B */
int main (int argc, char *argv[])
{
int tid, nthreads, i, j, k, chunk;
double a[NRA][NCA],
b[NCA][NCB],
c[NRA][NCB];
chunk = 10;
#pragma omp parallel shared(a,b,c,nthreads,chunk) private(tid,i,j,k)
{
tid = omp_get_thread_num();
if (tid == 0)
{
nthreads = omp_get_num_threads();
printf("Starting matrix multiple example with %d threads\n",nthreads);
printf("Initializing matrices...\n");
}
#pragma omp for schedule (static, chunk)
for (i=0; i < NRA; i++)
for (j=0; j < NCA; j++)
a[i][j] = i + j;
#pragma omp for schedule (static, chunk)
for (i=0; i<NCA; i++)
for (j=0; j < NCB; j++)
c[i][j] = 0;
printf("Thread %d starting matrix multiply...\n",tid);
#pragma omp for schedule (static, chunk)
for (i=0; i < NRA; i++) {
for (j=0; j < NCB; j++)
for (k = 0; k < NCA; k++)
c[i][j] += a[i][k] * b[k][j];
}
}
printf("******************************************************\n");
printf("Result Matrix:\n");
for (i=0; i < NRA; i++)
{
for (j = 0; j < NCB; j++)
printf("%6.2f ", c[i][j]);
printf("\n");
}
printf("******************************************************\n");
printf("Done\n");
}
Output
Starting matrix multiple example with 2 threads
Initializing matrices...
Thread 0 starting matrix multiply...
Thread 1 starting matrix multiply...
Thread=0 did row=0
Thread=1 did row=10
Thread=0 did row=1
Thread=1 did row=11
Thread=0 did row=2
Thread=1 did row=12
Thread=0 did row=3
Thread=1 did row=13
Thread=0 did row=4
Thread=1 did row=14
Thread=0 did row=5
Thread=1 did row=15
Thread=0 did row=6
Thread=1 did row=16
Thread=0 did row=7
Thread=1 did row=17
Thread=0 did row=8
Thread=1 did row=18
Thread=0 did row=9
Thread=1 did row=19
Thread=0 did row=20
Thread=1 did row=30
Thread=0 did row=21
Thread=1 did row=31
Thread=0 did row=22
Thread=1 did row=32
Thread=0 did row=23
Thread=1 did row=33
Thread=0 did row=24
Thread=1 did row=34
Thread=0 did row=25
Thread=1 did row=35
Thread=0 did row=26
Thread=1 did row=36
Thread=0 did row=27
Thread=1 did row=37
Thread=0 did row=28
Thread=1 did row=38
Thread=0 did row=29
Thread=1 did row=39
Thread=0 did row=40
Thread=1 did row=50
Thread=0 did row=41
Thread=1 did row=51
Thread=0 did row=42
Thread=1 did row=52
Thread=0 did row=43
Thread=1 did row=53
Thread=0 did row=44
Thread=1 did row=54
Thread=0 did row=45
Thread=1 did row=55
Thread=0 did row=46
Thread=1 did row=56
Thread=0 did row=47
Thread=1 did row=57
Thread=0 did row=48
Thread=1 did row=58
Thread=0 did row=49
Thread=1 did row=59
Thread=0 did row=60
Thread=0 did row=61
******************************************************
Result Matrix:
0.00 1015.00 2030.00 3045.00 4060.00 5075.00 6090.00
0.00 1120.00 2240.00 3360.00 4480.00 5600.00 6720.00
0.00 1225.00 2450.00 3675.00 4900.00 6125.00 7350.00
0.00 1330.00 2660.00 3990.00 5320.00 6650.00 7980.00
0.00 1435.00 2870.00 4305.00 5740.00 7175.00 8610.00
0.00 1540.00 3080.00 4620.00 6160.00 7700.00 9240.00
0.00 1645.00 3290.00 4935.00 6580.00 8225.00 9870.00
0.00 1750.00 3500.00 5250.00 7000.00 8750.00 10500.00
0.00 1855.00 3710.00 5565.00 7420.00 9275.00 11130.00
0.00 1960.00 3920.00 5880.00 7840.00 9800.00 11760.00
0.00 2065.00 4130.00 6195.00 8260.00 10325.00 12390.00
0.00 2170.00 4340.00 6510.00 8680.00 10850.00 13020.00
0.00 2275.00 4550.00 6825.00 9100.00 11375.00 13650.00
0.00 2380.00 4760.00 7140.00 9520.00 11900.00 14280.00
0.00 2485.00 4970.00 7455.00 9940.00 12425.00 14910.00
0.00 2590.00 5180.00 7770.00 10360.00 12950.00 15540.00
0.00 2695.00 5390.00 8085.00 10780.00 13475.00 16170.00
0.00 2800.00 5600.00 8400.00 11200.00 14000.00 16800.00
0.00 2905.00 5810.00 8715.00 11620.00 14525.00 17430.00
0.00 3010.00 6020.00 9030.00 12040.00 15050.00 18060.00
0.00 3115.00 6230.00 9345.00 12460.00 15575.00 18690.00
0.00 3220.00 6440.00 9660.00 12880.00 16100.00 19320.00
0.00 3325.00 6650.00 9975.00 13300.00 16625.00 19950.00
0.00 3430.00 6860.00 10290.00 13720.00 17150.00 20580.00
0.00 3535.00 7070.00 10605.00 14140.00 17675.00 21210.00
0.00 3640.00 7280.00 10920.00 14560.00 18200.00 21840.00
0.00 3745.00 7490.00 11235.00 14980.00 18725.00 22470.00
0.00 3850.00 7700.00 11550.00 15400.00 19250.00 23100.00
0.00 3955.00 7910.00 11865.00 15820.00 19775.00 23730.00
0.00 4060.00 8120.00 12180.00 16240.00 20300.00 24360.00
0.00 4165.00 8330.00 12495.00 16660.00 20825.00 24990.00
0.00 4270.00 8540.00 12810.00 17080.00 21350.00 25620.00
0.00 4375.00 8750.00 13125.00 17500.00 21875.00 26250.00
0.00 4480.00 8960.00 13440.00 17920.00 22400.00 26880.00
0.00 4585.00 9170.00 13755.00 18340.00 22925.00 27510.00
0.00 4690.00 9380.00 14070.00 18760.00 23450.00 28140.00
0.00 4795.00 9590.00 14385.00 19180.00 23975.00 28770.00
0.00 4900.00 9800.00 14700.00 19600.00 24500.00 29400.00
0.00 5005.00 10010.00 15015.00 20020.00 25025.00 30030.00
0.00 5110.00 10220.00 15330.00 20440.00 25550.00 30660.00
0.00 5215.00 10430.00 15645.00 20860.00 26075.00 31290.00
0.00 5320.00 10640.00 15960.00 21280.00 26600.00 31920.00
0.00 5425.00 10850.00 16275.00 21700.00 27125.00 32550.00
0.00 5530.00 11060.00 16590.00 22120.00 27650.00 33180.00
0.00 5635.00 11270.00 16905.00 22540.00 28175.00 33810.00
0.00 5740.00 11480.00 17220.00 22960.00 28700.00 34440.00
0.00 5845.00 11690.00 17535.00 23380.00 29225.00 35070.00
0.00 5950.00 11900.00 17850.00 23800.00 29750.00 35700.00
0.00 6055.00 12110.00 18165.00 24220.00 30275.00 36330.00
0.00 6160.00 12320.00 18480.00 24640.00 30800.00 36960.00
0.00 6265.00 12530.00 18795.00 25060.00 31325.00 37590.00
0.00 6370.00 12740.00 19110.00 25480.00 31850.00 38220.00
0.00 6475.00 12950.00 19425.00 25900.00 32375.00 38850.00
0.00 6580.00 13160.00 19740.00 26320.00 32900.00 39480.00
0.00 6685.00 13370.00 20055.00 26740.00 33425.00 40110.00
0.00 6790.00 13580.00 20370.00 27160.00 33950.00 40740.00
0.00 6895.00 13790.00 20685.00 27580.00 34475.00 41370.00
0.00 7000.00 14000.00 21000.00 28000.00 35000.00 42000.00
0.00 7105.00 14210.00 21315.00 28420.00 35525.00 42630.00
0.00 7210.00 14420.00 21630.00 28840.00 36050.00 43260.00
0.00 7315.00 14630.00 21945.00 29260.00 36575.00 43890.00
0.00 7420.00 14840.00 22260.00 29680.00 37100.00 44520.00
*************************************************************************
Done.
Given the trend towards bigger SMPs and multithreading computers, it is vital that strategies and techniques for creating shared-memory parallel programs become widely known. Explaining how to use OpenMP in conjunction with major programming languages like Fortran, C, and C++ to write such parallel programs is the purpose of this article.
References
- The Art of Concurrency, by Clay Breshears
