Introduction
Here is an interesting, but slightly detached from the previous two articles, result ...
Let's look at the following two sequences:
$a_{n}=\sqrt{p_{n+1}} - \sqrt{p_{n}}\\ b_{n}=\ln\left ( \frac{1+\sqrt{p_{n+1}}} {1+\sqrt{p_{n}}} \right )^{1+\sqrt{p_{n+1}}}$
Here is a short Python code to visualise the sequences:
import math
import matplotlib.pyplot as plt
primes = []
def isPrime(n):
l = int(math.sqrt(n)) + 1
for i in xrange(2,l):
if (n % i) == 0:
return False
return True
def calculateLog(sqrt_p1, sqrt_p2):
sqrt_1_p2 = 1.0 + sqrt_p2
r = math.log(sqrt_1_p2/(1.0 + sqrt_p1))
return r * sqrt_1_p2
N = 1500000
print "populate primes ..."
for i in xrange(2, N):
if isPrime(i):
primes.append(i);
sqrt_diff = []
diff = []
log_calcs = []
x = []
for i in xrange(1, len(primes)):
sqrt_p2 = math.sqrt(primes[i])
sqrt_p1 = math.sqrt(primes[i-1])
sqrt_diff.append(sqrt_p2 - sqrt_p1)
diff.append(primes[i] - primes[i-1])
log_calcs.append(calculateLog(sqrt_p1, sqrt_p2))
x.append(i)
for i in xrange(len(sqrt_diff)):
print sqrt_diff[i]," = s(",primes[i+1],") - s(",primes[i],")"
plt.subplot(311)
plt.plot(x, sqrt_diff)
plt.subplot(312)
plt.plot(x, log_calcs)
plt.subplot(313)
plt.hist(diff, 1000)
plt.show()
And here is how both sequences look like (\(a_{n}\) the first and \(b_{n}\) the second): 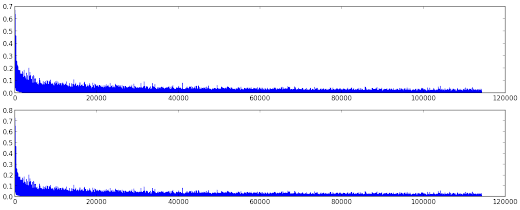
Quite asymptotic, aren't they? Indeed they are ...
Lemma 3.
$\sqrt{p_{n+1}} - \sqrt{p_{n}} \leq \ln\left ( \frac{1+\sqrt{p_{n+1}}} {1+\sqrt{p_{n}}} \right )^{1+\sqrt{p_{n+1}}} \leq \left ( \frac{1+\sqrt{p_{n+1}}} {1+\sqrt{p_{n}}} \right )\cdot \left ( \sqrt{p_{n+1}} - \sqrt{p_{n}} \right )$
Let's look at this function \(f_{6}(x)=\frac{\sqrt{p_{n+1}}}{1+x\cdot \sqrt{p_{n+1}}}\). Obviously \({\ln\left ( 1+x\cdot \sqrt{p_{n+1}} \right )}'=f_{6}(x)\) As a result
$\int_{\sqrt{\frac{p_ {n}}{p_{n+1}}}}^{1} f_{6}\left ( x \right )dx = \ln\left ( 1+x\cdot \sqrt{p_{n+1}} \right )|_{\sqrt{\frac{p_{n}}{p_{n+1}}}}^{1}=\ln\left ( \frac{1+\sqrt{p_{n+1}}} {1+\sqrt{p_{n}}} \right )$
According to Mean Value Theorem, \(\exists \mu \in \left (\sqrt{\frac{p_{n}}{p_{n+1}}} ,1 \right )\) such that:
$\int_ {\sqrt{\frac{p_{n}}{p_{n+1}}}}^{1} f_{6}\left ( x \right )dx = f_{6}\left ( \mu \right )\cdot \left ( 1- \sqrt{\frac{p_{n}}{p_{n+1}}} \right )$
Putting all together:
$\ln\left ( \frac{1+\sqrt{p_{n+1}}}{1+\sqrt{p_{n}}} \right ) = \frac{\sqrt{p_{n+1}} -\sqrt{p_{n}}}{1+\mu \cdot \sqrt{p_{n+1}}}$
Because:
$\sqrt{\frac{p_{n}}{p_{n+1}}}< \mu < 1 \Rightarrow 1+\sqrt{p_{n}}< 1+\mu \cdot \sqrt {p_{n+1}} < 1+\sqrt{p_{n+1}} $
And we get:
$\frac{\sqrt{p_{n+1}}-\sqrt{p_{n}}}{1+\sqrt{p_{n+1}}}\leq \ln\left ( \frac{1+\sqrt{p_ {n+1}}}{1+\sqrt{p_{n}}} \right )\leq \frac{\sqrt{p_{n+1}}-\sqrt{p_{n}}}{1+\sqrt{p_ {n}}}$
which proves this lemma.
Noting \(\Delta_{n}=\sqrt{p_{n+1}}-\sqrt{p_{n}}\), this becomes:
$\frac{\Delta_{n}}{1+\sqrt{p_ {n+1}}}\leq \ln\left ( 1 + \frac{\Delta_{n}}{1+\sqrt{p_{n}}} \right )\leq \frac {\Delta_{n}}{1+\sqrt{p_{n}}}$
or
$\frac{1+\sqrt{p_{n}}}{1+\sqrt{p_{n+1}}}\leq \ln\left ( 1 + \frac{\Delta_{n}}{1+\sqrt{p_{n}}} \right )^{\frac{1+\sqrt{p_{n}}} {\Delta_{n}}}\leq 1$
Is this result of any use? I don't know yet, but it looks like:
$\left ( 1 + \frac{\Delta_{n}}{1+\sqrt{p_{n}}} \right )^{\frac{1+\sqrt{p_{n}}} {\Delta_{n}}} \rightarrow e, n \to \infty$
