Tackling Andrica's Conjecture - Part 3

Introduction

Here is an interesting, but slightly detached from the previous two articles, result ...

Let's look at the following two sequences:

Here is a short Python code to visualise the sequences:

import math
import matplotlib.pyplot as plt

primes = []

def isPrime(n):
    l = int(math.sqrt(n)) + 1
    for i in xrange(2,l):
        if (n % i) == 0:
            return False
    return True

def calculateLog(sqrt_p1, sqrt_p2):
    sqrt_1_p2 = 1.0 + sqrt_p2
    r = math.log(sqrt_1_p2/(1.0 + sqrt_p1))
    return r * sqrt_1_p2

N = 1500000

print "populate primes ..."
for i in xrange(2, N):
    if isPrime(i):
        primes.append(i);

sqrt_diff = [] # sqrt diffs
diff = []      # simple diffs
log_calcs = [] # log calcs
x = []
for i in xrange(1, len(primes)):
    sqrt_p2 = math.sqrt(primes[i])
    sqrt_p1 = math.sqrt(primes[i-1])
    sqrt_diff.append(sqrt_p2 - sqrt_p1)
    diff.append(primes[i] - primes[i-1])
    log_calcs.append(calculateLog(sqrt_p1, sqrt_p2))
    x.append(i)

for i in xrange(len(sqrt_diff)):
    print sqrt_diff[i]," = s(",primes[i+1],") - s(",primes[i],")"

plt.subplot(311)
plt.plot(x, sqrt_diff)
plt.subplot(312)
plt.plot(x, log_calcs)
plt.subplot(313)
plt.hist(diff, 1000)
plt.show()

And here is how both sequences look like ($a_{n}$ the first and $b_{n}$ the second):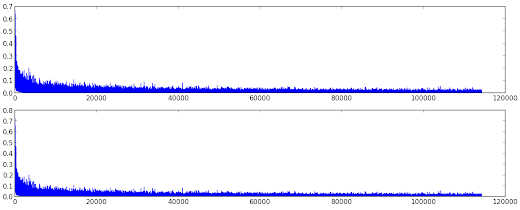

Quite asymptotic, aren't they? Indeed they are ...

Lemma 3.

Let's look at this function $f_{6}(x)=\frac{\sqrt{p_{n+1}}}{1+x\cdot \sqrt{p_{n+1}}}$. Obviously ${\ln\left ( 1+x\cdot \sqrt{p_{n+1}} \right )}'=f_{6}(x)$ As a result

According to Mean Value Theorem, $\exists \mu \in \left (\sqrt{\frac{p_{n}}{p_{n+1}}} ,1 \right )$ such that:

Putting all together:

Because:

And we get:

which proves this lemma.

Noting $\Delta_{n}=\sqrt{p_{n+1}}-\sqrt{p_{n}}$, this becomes:

or

Is this result of any use? I don't know yet, but it looks like: