Introduction
The trie is a family of tree data structures used to hold sorted sets or maps (dictionaries) in which each node of the tree only holds, or represents, parts of keys, not entire keys.
I am using a loose definition of "trie" here because I have developed a special kind of trie. I call it a "Compact Patricia Trie" or CPTrie. Unlike standard tries, which have very high memory requirements, CPTrie has lower memory requirements than other collection types, particularly in certain cases such as keys with a limited alphabet (e.g., ASCII text). It's generally slower than SortedDictionary and much slower than Dictionary, but it potentially uses much less memory than either of them.
So, while normal tries are sometimes used to build a sorted list quickly in exchange for high memory use, CPTrie provides the opposite tradeoff.
Please do read the Wikipedia article if you have never heard of tries; from now on, I'll assume you understand the concept.
Background
A few months ago, I read about something called the Judy array, a C sparse array data structure that organizes itself in one of several ways in order to keep itself both fast and memory-efficient at the same time. You can assign a value at any sequence of indices between 0 and uint.MaxValue, and Judy will organize itself into a kind of trie up to 4 levels deep (one level for each byte of the index), that is always fast and memory efficient regardless of the key distribution. For example, if you assign a value at every index between 0 and 1000, Judy will produce a data structure similar to an ordinary array, so that the values are closely packed. Meanwhile, if you use clusters of indices, say 23-70, 200-210, and 500-550, with a few unused slots, Judy will choose a different arrangement called a "bitmap". In any case, it minimizes the number of processor cache lines that are accessed.
Thanks Judy...
I was so captivated by Judy's ideas that I wanted to make something like it for .NET, but after thinking and coding for several days, I came to the conclusion that there was no way, in C#, to come close to the speed or memory efficiency of Judy.
For example, Judy often stores data inside pointers. The bottom 2 or 3 bits of any pointer to any heap block is always zero; so you can either use those bits to store information along with the pointer, or you can use one of those bits to indicate that the pointer holds an integer instead. The dynamic language Ruby uses this technique to store integers in variables. That way, a variable can either point to an object, or (if the low bit is 1) it can store an integer directly with no heap space required. Sadly, this seems to be outright impossible in C#, even with unsafe code, since the garbage collector would probably crash when it encounters one of these non-pointers.
Another important limitation of C# is that you cannot store a fixed-length array of object[] inside a class--you can only use fixed-length arrays of primitive types. Even then, you must sprinkle the unsafe keyword everywhere so the code would be unusable in "safe" contexts. An external object[] array is distinctly less efficient, as it requires a 4-DWORD header and may need one extra cache line to access. Oh, and in .NET, the allocation alignment of ordinary objects cannot be controlled, so it is difficult to align to cache line boundaries.
...I left you for Patricia
Then, after reading about Burst tries and Patricia tries, I decided maybe there was hope that I could make some kind of useful new data structure for .NET. Plus, while porting some C++ code to C#, I was irritated because there was no .NET equivalent for map::lower_bound, and I figured I would solve that problem too.
Introducing the CPTrie
CPTrie combines...
- the Patricia trie idea of storing multi-byte prefixes in a single node
- the Burst trie idea of storing a limited number of keys together without factoring out common prefixes
- the Judy ideas of using multiple node types, storing data in a very compact form, and gaining speed by being cache-friendly
I guess I could have called it the PBJ trie. That would have been yummy.
I also wanted to use the Judy idea of using different types of nodes for different key densities, but I couldn't figure out an efficient way to port Judy's "bitmap" and "uncompressed" nodes to .NET, under the constraint that I wanted to support variable-length keys. But I'm really getting ahead of myself.
CPTrie itself is an abstract base class that only understands keys as arrays of bytes. Each kind of key you want to support needs a derived class to translate keys into byte arrays. In order to store strings in a CPTrie, I provide the CPStringTrie class. When you store a string in CPStringTrie, the string is encoded in UTF-8 format before being placed in the trie. To store integer keys, use CPIntTrie. If you actually want to use byte arrays as keys, use CPByteTrie.
If you use CPStringTrie to hold strings, it will likely end up as a tree of "sparse" (a.k.a. "standard") nodes (CPSNode). When using CPIntTrie, up to three different kinds of nodes are used depending on the distribution of keys. Small collections (regardless of key distribution) always use CPSNodes.
It helps to explain the structure of a CPTrie in picture form. Suppose you run the following code:
CPStringTrie<int> t = new CPStringTrie<int>();
t["This little piggy went to market"] = 1;
t["This little piggy stayed at home"] = 2;
t["This little piggy had roast beef"] = 3;
t["This little piggy had none"] = 4;
t["And this little piggy went"] = 5;
t["'Wee wee wee' all the way home."] = 6;
t["And then some wolf came along"] = 7;
t["and blew down two of their houses!"] = 8;
CPStringTrie will end up containing two nodes, structured as follows:

As you add keys, the node must either enlarge itself or split itself (creating a child node), to make room for new keys and values. At first, it will enlarge itself, but at some point, it will notice a common prefix and decide to create a child node instead.
Notice that the trie is sorted, but the sort order is case-sensitive (uppercase comes before lowercase, the natural order of ASCII). Unlike a SortedDictionary, which supports various sort orders, case-sensitive sorting is an inherent limitation of a trie (a kind of workaround is possible, but I have not tried it).
Like a Patricia trie, CPSNode can hold several bytes of a key within a single node. Somewhat like a Burst trie, CPSNode does not immediately create new nodes when two keys have a common prefix, because it is more efficient to wait until there are several keys before splitting the node. Unlike a Burst trie, however, a CPSNode splits by creating children, not by creating a new parent node.
Nitty-gritty details (skip if you don't care)
CPSNode<T>: the "standard" or "sparse" node
A CPSNode<T> consists of:
- An array of "cells" (
SCell[]) which are used to encode parts of keys - An array of "children" (
CPNode[]) which associate child nodes with common prefixes - An array of "values" (
T[]) associated with keys that terminate in the current node (i.e., keys that do not have children)
Some nodes have no children, so the array of children may be null. Likewise, there may be no values; in fact, storage is not allocated for the null value, so if you want to store a set of strings instead of a dictionary, use null for all values to save memory.
The cell is the innovative part that allows nodes to be very compact. Normal .NET strings take up a relatively large amount of space, because each string has a 12-byte header as well as a 2-byte null terminator and sometimes 2 bytes of padding (in a 32-bit process, I think). Moreover, if the text is English, half the space is wasted on null bytes of UTF-16. By encoding several strings into a single array of "cells", only one 12-byte header is needed for all the strings, and there are no null terminators.
Cells are 4-byte groups that encode partial (or complete) keys and pointers to values or child nodes. If a CPSNode contains _count keys (or partial keys), the first _count cells are sorted and describe the beginning of those keys. Each cell contains up to 3 bytes of a key (K0, K1, and K2), so the first _count cells tell us the first three bytes of each key. The fourth byte, called P, acts as a pointer to another cell, to a child, or to a value, depending on its value:
- A child node (if
P < _count); [P] is an index into the child array - Another cell (if
P < 222); [P] is an index into the cell array - A non-null value (if
P < 254), where [253-P] is an index into the value array - The null value (if
P == 254)
If P == 255, it means that the cell is free, and it is part of a doubly-linked list of cells that are not in use.
Because P is only one byte, the size of a CPSNode must be fairly limited. There are a maximum of 32 values; all keys together cannot use more than 222 cells; and I arbitrarily selected limits of 34 for _count and 50 bytes for the length of any single key*. The number of keys in a single node must be strictly limited anyway, because the first _count cells form a sorted array, and building a sorted array with N items requires O(N2) time. Building an unsorted array first and sorting it afterward would be faster (O(N log N)), but for various reasons, that seems impractical. The limit should not be too low either, because as the number of keys decreases, CPSNode becomes less memory-efficient as more objects and arrays are allocated, leading to more overhead. Also, traversing from one node to another may take extra time, as the processor stalls more often waiting for cache lines to fill.
* Note: I am not saying keys are limited to 50 bytes, only that keys longer than 50 bytes will be broken up into a chain of nodes.
If P points to a value or child node, the key might not use the entire three bytes that are available in that cell. Special values of K2 indicate this situation; for instance, K2==254 means that the key ends after only one byte (K0). Of course, if the number 254 actually happens to be the third byte of the key, special handling is required.
There can be (at most) one zero-length key in any given node, but there can sometimes be a zero-length cell following a cell of length three, in some cases, where a special number like 254 is encountered at the end of a key.
CPBNode<T>
Since a CPSNode can contain up to 34 items, it can comfortably hold a set of words starting with each letter of the alphabet (e.g., "apple", "banana", "coconut", donut", etc.). However, if there are more than 34 different characters at the beginning of the keys (or following a common prefix), a different data structure is required.
I would have liked to do something resembling Judy's "bitmap nodes", but I couldn't think of a very efficient way to do it in .NET. So instead, I implemented a simple kind of bitmap node that I call CPBNode. CPBNode simply divides the "byte space" into 8 slices, with a child CPSNode for each slice. There is a CPSNode for keys that start with a byte between 0 and 31 (child #0), another CPSNode for keys between 32 and 63 (child #1), and so forth. This way, there can never be more than 32 unique starting bytes in any given child. When CPBNode is asked to create a key such as "~foo~", it observes that '~' (0x7E) is in slice #3, so it forwards the "create" request to child #3. If some slices are not needed (e.g., if there are no non-ASCII characters), CPSNodes are not allocated for unused ranges.
CPBNode will switch back to CPSNode when the number of items drops below 24. CPBNode never converts itself to CPBitArrayLeaf.
CPBitArrayLeaf<T>
CPBitArrayLeaf is a new node type I added to improve the space efficiency of CPIntTrie when densely packed keys are detected, i.e., when sequences of integers are close together. CPBitArrayLeaf is also the fastest node type. Theoretically, string tries can also use this node type, but only when there are a large number of constant-length strings that differ only in their last character.
As its name implies, CPBitArrayLeaf is a leaf node with an array of bits (called _flags). It only supports 1-byte keys, and the bit array has two bits for each of the 256 possible keys. There is also an array of _values (type T[]) and a table of _indices that map keys to slots in the _values array. _flags is really two arrays of 256 bits: one array tracks which keys are in use, and the other tracks which entries in _values are in use, so that a free slot can be found quickly.
If a key is ever added that is not 1 byte, the node must be converted immediately to CPSNode or CPBNode.
CPBitArrayLeaf has a fixed size for keys - the number of non-null values affects its size, but the number of keys does not. Therefore, CPBitArrayLeaf is very efficient when it is almost full (near 256 keys), but inefficient when it is nearly empty (near 0 keys).
Normally, CPSNode switches to CPBitArrayLeaf when it is full with 34 items and every key is one byte (with no children); CPBitArrayLeaf switches back if the number of items drops below 24, which is the approximate point at which both node types occupy the same amount of memory. However, CPBitArrayLeaf is more compact when there are no values associated with the keys, because of the overhead of the _indices map. Therefore, if you are storing a set (with all null values) rather than a dictionary, CPSNode will switch to CPBitArrayLeaf at 16 items and switch back to CPSNode when the number of items drops below 12.
Deletions
CPTrie is quite memory-efficient if you only insert nodes, but what about deletions? Well, rest assured, deleting keys is as fast as inserting them... at least I think so, but I didn't make a benchmark for it. However, after deleting the majority of keys, the trie may have a less efficient structure.
Remember, during insertion, a node is not eager to divide because multiple small nodes are typically less efficient than one large node. This is because if nodes are small, a larger fraction of their size goes to .NET object headers, and on average, more nodes must be traversed when scanning a key (keys are "scanned" as we insert, remove, find, or enumerate them). When deleting keys, small nodes are not consolidated into larger nodes; a small node is only eliminated when its last key is removed.
The worst case is not terrible, however. In the worst case, after removing most of the nodes from a very large CPTrie, the "Patricia trie" property can be lost, increasing the space overhead. But tries cannot be "unbalanced" the way a binary search tree can be, so it is not crucial for CPTrie to have a balancing algorithm. CPSNode does notice when the majority of its cells are unused, and it will switch to a smaller array in that case.
Optimizing the trie
You may have heard that as you add items to a List<T>, the items are added to a fixed-size internal array. When that array is full, List<T> copies the items to another array that is twice as big, before discarding the original array.
CPSNode<T> does roughly the same thing for each of its arrays (_cells[], _children[], and _values[]); consequently, there are usually some unused array entries sitting around, wasting space.
CPTrie can optimize itself when it makes a copy of itself, so you can eliminate this space by calling Clone() and then discarding the original version of the trie. Unfortunately, at this time, it does not support optimizing in-place, so when you make the clone, memory will be required for the original trie and its clone simultaneously (which is only a problem if the trie is extremely large).
In some applications, you will build a trie and then scan it many times without modifying it at all. In such cases, you should optimize the trie. Note that the optimization process merely discards unused array entries; it does not optimize the structure of the trie (e.g., to account for deleted items).
My benchmark program shows that an optimized CPTrie tends to be about 20% smaller.
In a program (such as my benchmark) that uses datasets larger than the processor cache, I have found that an optimized CPTrie is about 10% faster when looking up keys. I believe this is for two reasons related to locality of reference:
- Because there are fewer blank spaces in the cells array, a key longer than 3 bytes, but in the same cell array, is more likely to be on the same cache line.
- An optimized trie node allocates all three of its arrays together. The .NET memory manager tends to put objects adjacent in memory when they are allocated at the same time, so the node itself and its three arrays are likely to be contiguous in memory. Therefore, they share some cache lines and can be accessed with fewer processor stalls.
When should you use a trie?
When managing any large amount of data, it's important to choose the right data structure for the job. If your keys are not strings and can't be represented as a byte array, then you can't use CPTrie anyway. If you do not need to access keys in sorted order, you are probably best off using a hash table. .NET's Dictionary<K,V> is an excellent hash table design that is both simple (small code size) and fast.
If you need keys in sorted order, but not until all the keys are added to the list, it might still be better to use a standard Dictionary, or even a List<KeyValuePair<K,V>>, because both of those are so much faster than SortedDictionary and CPTrie. Add all your key-value pairs to the Dictionary or List, then (if you used Dictionary), call ToList() to convert it to a List, then sort the list with List<T>.Sort().
On the other hand, if you need interleave queries (that depend on the sort order) with modifications to the collection, SortedDictionary and CPTrie make sense. If you need to sort strings in case-insensitive or culture-sensitive order, you should probably use SortedDictionary.
In some cases, you should consider some kind of parallel data structure or algorithm (standard Dictionary, SortedDictionary, and CPTrie are all single-threaded).
Okay, so when should you use CPTrie?
One reason to use CPTrie is that it offers four operations that SortedDictionary lacks:
- Reverse-order enumeration: get an enumerator from
GetEnumerator(), then call MovePrev() repeatedly instead of MoveNext(). - Find the nearest larger key: call
Find() or FindAtLeast() to get an enumerator that points to the key equal to or greater than the requested key. - Get the next key/value and get the previous key/value:
SortedDictionary will only let you get the next key if you start enumerating from the beginning. With CPTrie, you can start enumerating (backward or forward) from any key you want.
There is no reason SortedDictionary couldn't offer these operations, but for some reason, it doesn't.
Here are some more reasons to consider CPTrie:
- Your keys have many common prefixes. For example, a set of URLs all start with one of a few prefixes, such as "http://", "http://www.", "ftp://", "file:///", and so forth. In such cases,
CPTrie will store the common prefix only once, saving a lot of memory in a large set. In such cases, SortedDictionary has lookup speed of at worst O(K log N) (where K is the key length and N is the collection size), whereas CPTrie is no worse than O(K). - Your data set is extremely large, and you need to avoid using more virtual memory than physical RAM. For instance, if the machine has 1 GB of RAM, the computer will slow to a crawl when your data structure exceeds that size. In a 32-bit Windows process, you can't normally use more than 2 GB total; if you might approach that limit, consider
CPTrie. In some cases, CPTrie can encode the trie itself and all the keys in the same amount of memory it takes Dictionary and SortedDictionary to hold the data structure and merely pointers to the keys. Provided that you do not need to store copies of the keys in string form, you can often use half the memory by using CPTrie (see graph below). - You need a set, not a dictionary, and you are not using .NET 4.0 (which offers a sorted set collection). If you use a reference type as the value type of a
CPTrie, CPTrie will save at least 4 bytes of memory every time you use null as the value for a key. This allows CPTrie to store sets very compactly. - You want to store a set of integers that are highly clustered, meaning that there are long runs of almost-consecutive integers, e.g., 1, 2, 3, 4, 5, 7, 8, 9, 97, 98, 99, 101, 102, 104, etc.
CPIntTrie can store large clusters efficiently with CPBitArrayLeaf nodes, especially if no values need to be associated with the integers.
Performance for string storage
I compared CPStringTrie to Dictionary and SortedDictionary for three data sets:
- A list of English words from 12dicts.
- A collection of 200,000 strings. Each key was built by concatenating two random English words with a space in between.
- A collection of 1,000,000 strings. Each key was built by concatenating one of 31 prefixes to a random English word with a space in between. In the second test, I expect the
CPTrie to receive some benefit (in speed and space) from the relatively small number of prefixes.
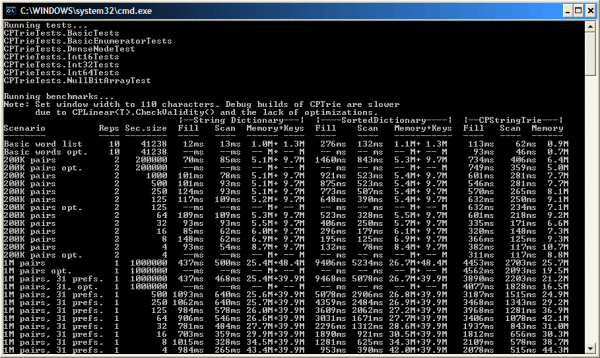
You can see the results of the first data set in the first two lines of the benchmark in the screenshot at the beginning of this article (or, just run the benchmark on your own machine - be sure to use a Release build). The first line uses a normal non-optimized CPTrie, while the second line (marked "opt.") shows the performance difference when the trie is optimized, but since the English word list fits in my processor's 2 MB cache, it doesn't make much difference.
Speed
After first publishing this article, I realized I had not been fair to SortedDictionary because I had used the default sort order. Since CPStringTrie sorts by ordinal, SortedDictionary ought to use the StringComparer.Ordinal comparer instead, to make the comparison fair. This change makes SortedDictionary about twice as fast, so CPStringTrie is generally slower for collections with less than 200,000 items, but it is still faster for very large collections.
The timer used for measurements has a 10-15ms. resolution, so the tests on the first data set are repeated 10 times to get more accurate results. For the larger data sets, I only used 1 or 2 reps so that the benchmark didn't take too long.
I only benchmarked the speed of insertions and retrievals ("scanning"). There are no benchmarks for enumeration or removals. I suspect that CPTrie has relatively slow enumeration because when you ask for the value of each key, it must be converted from byte[] to string, whereas Dictionary and StringDictionary store strings directly. However, I don't expect removals to be slow.
For the last two data sets, I did a sequence of tests to show the effect of varying collection sizes. In the first test of each data set, I stored the entire data set (200,000 or 1,000,000 items) in a single collection. For the other tests, I divided the data set into "sections" of size 1000, 500, 250, or smaller, and I placed each section in its own collection. This is intended to simulate common applications that manage large amounts of data but do not store all the data in one place--that is, the data is spread out over many collections.
Only the first data set is small enough to (almost) fit in a typical 2 MB L2 cache. In all other cases, I tried to access the data in such a way that the processor cache is stressed. Before scanning the keys, their order is randomized, and one key is added or retrieved from each collection in turn, so that the cache tends to be "cold" when retrieving each key. I thought this access pattern would be relatively friendly to CPTrie because of its compact size, but it doesn't seem to matter much.
So, here are the results:


These graphs show that (on my workstation) CPTrie only beats StringDictionary for very large collections. Note that StringDictionary must be constructed with ordinal sort order for this to be true; the default sort order (which I think is case insensitive and culture-aware) cuts StringDictionary's speed in half. In any case, StringDictionary gets incrementally slower as the collection size increases, which makes sense because it uses a red-black tree, which requires O(log N) time for each insertion or retrieval.
CPTrie has a more complex insertion performance. Insertion speed suddenly becomes slower for collections with 64 rather than 32 items; I suspect this is because the trie is forced to split into multiple nodes after it exceeds its 34-item-per-node limit, and the splitting process is somewhat expensive. However, performance never gets much worse; a collection with 200,000 items is constructed almost as fast as 1600 collections with 125 items each.
It almost seems as though CPTrie defies the law I was taught in school that sorting algorithms generally cannot be faster than O(N log N). Yet theoretically, I believe a trie can produce a sorted data set in O(N * K) time, where K is the (average?) key length, and there is no "log N" penalty. Does some academic care to explain this discrepancy?
Memory
As I mentioned, CPTrie can use less memory than standard collections, and it does especially well for large data sets.
I performed memory measurements in a purely analytical way, under the assumption of a 32-bit processor. To determine the memory use of these collections, I assumed 8-byte headers on normal objects, 12- and 16-byte headers on arrays (see here), 4-byte object alignment and standard alignment rules, and then I examined each of the relevant classes to figure out its memory requirements.
For CPTrie, I wrote a method (CountMemoryUsage()) to compute the exact memory usage; for Dictionary and SortedDictionary, I used Reflector to examine the implementation details to find out how much memory is used, and I wrote methods to calculate memory use. If you trust my arithmetic, the memory measurement for SortedDictionary is exact, whereas Dictionary is only approximate. Dictionary, like List<T>, uses arrays that roughly double in size when they are enlarged, which means that between 0% and 50% of entries in a Dictionary are unused. A Dictionary cannot be asked for its current capacity, so for my calculation, I assumed that 25% of the entries were unused.
If you are using a 64-bit process instead, I suspect CPTrie will look relatively more favorable, although all types of collections will require substantially more memory.
So, here are the memory graphs to go along with the speed graphs above. The trie measurements are for a non-optimized trie.
There is an important "cheat" here: the memory consumption of the keys is added to the total memory use of the Dictionary and SortedDictionary, but not for the CPStringTrie. So, while it appears CPTrie uses less memory, this is only true if you discard the keys after adding them to the trie. If you keep all the keys lying around in the form of strings (as the benchmark does, admittedly), you will not save memory by using CPStringTrie!


So, keeping in mind the rule about keys, the 200,000 item CPStringTrie can use 57% less memory than the Dictionary, assuming 4-byte values associated with each key. The million-item trie is even better, using 67% less memory.
I thought that the million-item trie would save quite a bit of memory by having only 31 prefixes, but if I use random word pairs instead (not shown on the graph), the savings is still a healthy 65% compared to the Dictionary. Note that there are only 41,238 unique words, so there are still many common prefixes in the million-item test.
If you optimize your trie with Clone() after you are done building it, you can save about 20% more memory than shown on the graphs, plus you'll get 10% faster queries if your access pattern stresses the processor cache (but you'll take a performance hit if you modify the trie after optimizing it). Notice the memory spike for collections with 64 items - I believe this happens because most of the 32-item tries fit in one node, but the 64-item tries require two or more, increasing overhead disproportionately. All three collection types require more memory if there are very few items per collection (because the sheer number of collections is very high, and each one has some overhead).
Remember that in these tests, the keys are ASCII. This helps save memory because CPStringTrie uses UTF-8, compared to normal UTF-16 strings which use two bytes per character. However, if you store mainly non-ASCII strings such as Chinese, CPStringTrie will need substantially more memory (I believe a typical Chinese character uses 3 bytes in UTF-8 versus 2 for UTF-16).
CPIntTrie
I wrote a single class, CPIntTrie<TValue>, for storing integers of all sizes from 8 bits to 64 bits, signed or unsigned. It contains overloaded methods for adding integers of various sizes, and it implements two dictionary interfaces, IDictionary<int, TValue> and IDictionary<long, TValue>, which should cover most use cases.
In order to store data efficiently in CPSNodes, CPIntTrie encodes each key into bytes in one of three formats:
- A 3-byte form for 24-bit integers in the range -0x10000 to 0xFAFFFF
- A 6-byte form for 41-bit integers in the range -0xFFFFFFFFFF to 0xFFFFFFFFFF
- A 9-byte form for large signed and unsigned integers
Using multiples of 3 bytes makes sense for storing numbers in a CPSNode, where there are 3 bytes per node. In large collections, the encoding method is not really important as long as it maintains sort order, but in small collections, this encoding is as compact as possible.
To maintain sort order, all the 6-byte negative integers need to appear "smaller" than the 3-byte ones, and all the 6-byte positive integers need to appear "larger". Likewise, the negative 9-byte integers need to appear the smallest, and positive 9-byte integers need to appear the largest. Therefore, the keys are stored in a kind of big-endian format, with a prefix byte in front that indicates magnitude and length:
- 0x00: 64-bit signed integer below -0xFFFFFFFFFF in 9 bytes
- 0x01: 41-bit signed integer between -0xFFFFFFFFFF and -0x10000 in 6 bytes
- 0x02-0xFD: 24-bit integer between -0x10000 and 0xFAFFFF in 3 bytes; subtract 3 from this byte to compute the first byte of the 24-bit number
- 0xFE: 40-bit unsigned integer between 0xFB0000 and 0xFFFFFFFFFF in 6 bytes
- 0xFF: 64-bit unsigned integer above 0xFFFFFFFFFF in 9 bytes
The original data type is not encoded: the "byte" 100 and the "int" 100 are stored the same way. Although it would be very unusual to use signed and unsigned 64-bit numbers as keys simultaneously in the same collection, CPTrie does allow it. Therefore, there is no primitive data type that can represent all possible keys.
Performance for integer storage
For the integer benchmarks, I took a different approach than the string benchmarks. In the string benchmarks, I examined how the trie's performance is affected by collection size, by repeating the tests with keys divided into "sections" of various sizes. I simplified the integer benchmarks by only testing a single large collection at once, but I used a variety of key distributions, thinking this could affect performance and space consumption of the trie.
Speed
The executive summary: CPIntTrie is usually slower than SortedDictionary. However, if the keys are very densely clustered, CPIntTrie is faster and much smaller. CPIntTrie is also a good choice for very large collections. However, as before, Dictionary is much faster than either of the sorted collections.
I did tests involving 24-bit, 32-bit, and 64-bit keys. I tried three kinds of key distribution:
- Random: a uniform distribution.
- Exponential: in 32-bit mode, a random number is chosen with a random number of bits between 15 and 32 so that the high bits are zero; this should approximate picking a random point on a logarithmic scale. In 64-bit mode, a random 32-bit number is left-shifted by up to 32 bits.
- Clustered: clusters are groups of integers that are close together. But how close? There are an infinite number of variations of the idea of "clustered" data. In my tests, I build random clustered key sets using parameters
(C, S, D, start) where C is the maximum number of integers in each cluster (C/2 is the minimum), S is the maximum space between clusters (S/2 is the minimum), D is the maximum distance between adjacent integers in the cluster (1 is the minimum), and start is the first integer in the series (start is set to 0x0123456789ABCDEF for 64-bit clusters, and 0x1000000 for 32-bit clusters). I picked various arbitrary values for C, S, and D in the tests. Clustered data often appears in ID columns of databases. Each new row is given an ID one greater than the last, but over time, some rows or series of adjacent rows are deleted, leaving small or large gaps in the integer space. CPIntTrie stores such sets very compactly. Clustered data also come from various other sources, such as histograms.
Of course, the key distribution has little or no effect on the performance of Dictionary or SortedDictionary. CPIntTrie, it turns out, is usually not dramatically affected by the key distribution either, except that CPIntTrie handles densely clustered data faster, and it is faster when storing a set (null values) rather than a dictionary.
Here's some raw data from my machine:
|-Int Dictionary--| |-SortedDictionary-| |----CPIntTrie----|
Scenario Reps Set size Fill Scan Memory Fill Scan Memory Fill Scan Memory
-------- ---- -------- ---- ---- ------ ---- ---- ------ ---- ---- ------
1-100,000, sorted 10 100000 15ms 12ms 2.5M 128ms 58ms 2.7M 63ms 46ms 0.9M
1-100,000, random 10 100000 15ms 4ms 2.5M 132ms 62ms 2.7M 58ms 44ms 0.9M
1-100,000 w/ null vals 10 100000 15ms 6ms 2.5M 129ms 58ms 2.7M 47ms 43ms 0.0M
24-bit keys with 100K items:
Random 24-bit ints 10 100000 19ms 9ms 2.5M 134ms 66ms 2.7M 157ms 65ms 2.0M
Random set (null vals.) 10 100000 18ms 13ms 2.5M 134ms 62ms 2.7M 117ms 63ms 1.3M
Clusters(20, 100,2) 10 100000 15ms 9ms 2.5M 134ms 66ms 2.7M 101ms 60ms 2.2M
Clusters(same w/ nulls) 10 100000 18ms 9ms 2.5M 135ms 63ms 2.7M 81ms 46ms 0.2M
Clusters(20, 100,9) 10 100000 16ms 9ms 2.5M 131ms 60ms 2.7M 134ms 65ms 2.3M
Clusters(20,1000,2) 10 100000 21ms 9ms 2.5M 131ms 63ms 2.7M 126ms 70ms 1.4M
Clusters(20,1000,9) 10 100000 15ms 12ms 2.5M 132ms 55ms 2.7M 129ms 74ms 1.4M
Clusters(50, 100,2) 10 100000 15ms 10ms 2.5M 129ms 60ms 2.7M 84ms 47ms 1.6M
Clusters(50, 100,9) 10 100000 21ms 12ms 2.5M 132ms 58ms 2.7M 128ms 52ms 3.1M
Clusters(50,1000,2) 10 100000 15ms 12ms 2.5M 131ms 62ms 2.7M 137ms 62ms 1.7M
Clusters(50,1000,9) 10 100000 16ms 10ms 2.5M 128ms 58ms 2.7M 143ms 70ms 2.2M
Tests with 32-bit keys:
Random 32-bit ints 10 100000 23ms 16ms 2.5M 154ms 58ms 2.7M 175ms 96ms 2.0M
Random 32-bit ints 5 200000 49ms 43ms 5.1M 315ms 165ms 5.3M 468ms 237ms 5.1M
Random 32-bit ints 3 500000 135ms 130ms 12.7M 1051ms 530ms 13.4M 1291ms 614ms 8.5M
Random 32-bit ints 2 1000000 335ms 281ms 25.4M 2593ms 1257ms 26.7M 2390ms 1328ms 13.3M
Exponential 32-bit 10 100000 21ms 13ms 2.5M 134ms 62ms 2.7M 185ms 88ms 1.9M
Exponential 32-bit 5 200000 49ms 49ms 5.1M 321ms 162ms 5.3M 390ms 218ms 3.8M
Exponential 32-bit 3 500000 140ms 135ms 12.7M 1056ms 525ms 13.4M 1234ms 567ms 9.1M
Exponential 32-bit 2 1000000 335ms 288ms 25.4M 2671ms 1218ms 26.7M 2601ms 1218ms 17.8M
Clusters(25,25,1) 10 100000 15ms 0ms 2.5M 129ms 62ms 2.7M 81ms 62ms 1.5M
Clusters(25,30000,5) 10 100000 16ms 10ms 2.5M 134ms 60ms 2.7M 155ms 93ms 1.3M
Clusters(50,50000,5) 10 100000 16ms 12ms 2.5M 134ms 60ms 2.7M 180ms 90ms 2.0M
Clusters(75,90000,5) 10 100000 19ms 9ms 2.5M 129ms 60ms 2.7M 169ms 82ms 2.1M
Clusters(75,90000,5) 5 200000 40ms 40ms 5.1M 318ms 165ms 5.3M 368ms 205ms 4.3M
Clusters(75,90000,5) 3 500000 130ms 130ms 12.7M 1031ms 530ms 13.4M 1202ms 577ms 10.6M
Clusters(75,90000,5) 2 1000000 320ms 296ms 25.4M 2624ms 1241ms 26.7M 2562ms 1234ms 21.3M
Clusters(75,90000,5) 1 2000000 687ms 593ms 50.9M 6671ms 2796ms 53.4M 5265ms 2656ms 42.7M
Clusters(99,90000,2) 1 2000000 703ms 578ms 50.9M 6640ms 2796ms 53.4M 5328ms 3062ms 28.1M
Tests with 64-bit keys:
Clusters(25,50000,9) 10 100000 23ms 15ms 3.1M 151ms 71ms 3.1M 177ms 97ms 1.4M
Clusters(50,20000,5) 10 100000 23ms 15ms 3.1M 148ms 68ms 3.1M 179ms 91ms 2.0M
Clusters(75,1000,3) 10 100000 19ms 13ms 3.1M 144ms 71ms 3.1M 156ms 70ms 1.8M
Random 32-bit longs 10 100000 26ms 15ms 3.1M 149ms 71ms 3.1M 179ms 96ms 2.0M
Random 40-bit longs 10 100000 24ms 15ms 3.1M 174ms 78ms 3.1M 190ms 93ms 2.5M
Random 64-bit longs 10 100000 26ms 15ms 3.1M 148ms 68ms 3.1M 201ms 94ms 3.1M
Random set (null vals.) 10 100000 27ms 16ms 3.1M 144ms 71ms 3.1M 187ms 90ms 2.3M
Exponential longs 10 100000 26ms 15ms 3.1M 154ms 74ms 3.1M 210ms 112ms 2.3M
Exponential longs 5 200000 55ms 46ms 6.1M 365ms 187ms 6.1M 534ms 246ms 4.7M
Exponential longs 3 500000 156ms 135ms 15.3M 1296ms 567ms 15.3M 1406ms 697ms 11.4M
Exponential longs 2 1000000 343ms 296ms 30.5M 3218ms 1452ms 30.5M 3343ms 1531ms 22.3M
I only made a graph of the 32-bit section of these results:

Note that this graph doesn't show cases of all-null values, which are faster, but you can see that the dense cluster (25,25,1) is faster than SortedDictionary.
Memory
Compared to CPStringTrie, CPIntTrie's memory savings are not as dramatic, but still distinct. The graph below shows how CPIntTrie handles various distributions and data sizes of 32-bit integers.
The graph doesn't show any cases of null values. If you look at the raw data, you'll see that in cases where all values are set to null (e.g., "1-100,000 w/ null values"), dramatically less memory may be required, particularly if the data is densely clustered. In such cases, the trie acts more like a bit array in regions of the integer space that contain dense clusters of keys. In the best such case, less than 4 bits per key are required, so the total comes to 0.0 MB after rounding to the nearest 0.1 MB. You can choose whether or not to use a value on a key-by-key basis, but in order to get such dramatic memory savings, large regions of the number space must only use null values.

Curiously, there is a spike in memory usage for the case of 200K random integers. I am not certain why this is the case, but I suspect the key density is the problem. CPTrie is efficient when the keys are either sparse (using CPSNode) or dense (using CPBitArrayLeaf), but at certain densities, it would have to use CPBNode, and since the data is random, it requires 8 CPSNodes per CPBNode, which adds a lot of overhead.
On the other hand, memory use dips for 1 million random numbers and for certain kinds of clustered data. In the case of 1 million random integers, I can only assume this key density is a sweet spot, even though it is not dense enough to use CPBitArrayLeaf. The clusters (25,25,1) and (99,90000,2) are probably benefiting from CPBitArrayLeaf, while perhaps the clusters (25,30000,5) make efficient use of CPSNode leaves.
The end
I hope you enjoyed reading about my new data structure. Let me know if you find a practical application!
History
- March 30, 2010: Added
CPIntTrie (and CPBitArrayLeaf) with benchmarks and tests. - February 26, 2010: Initial release with
CPStringTrie and CPByteTrie.
