A Simple - Yet Quite Powerful - Palette Quantizer in C#

• Download source (version 1.0) - 28.53 KB
• Download source (version 2.0) - 48.96 KB
• Download source (version 3.0) - 57.06 KB
• Download source (version 4.0) - 77.81 KB
• Download source (version 5.0) - 115.92 KB (NEW)

Introduction 

This article presents a color quantizer, which is simple to understand for beginners, yet powerful enough for every day use. From version 2.0, it contains the optimized version, and also implementation of other common quantizers for you to use. From version 4.0, it also contains different color matching algorithms for better practical usability. In version 5.0 the support for dithering, and parallel processing was added (see change log for more details).

Background

I was searching for a good color quantization algorithm, and my first stop was of course The Code Project. I found many quantizers, but all of them were quite similar. They're all based on octree, and were all reducing a palette inaccurately. I needed something - more of a Swiss knife quantizer, that will reduce a palette even for the 1-bit color depth reasonably. It has to be fast enough, precise enough and also the results must be above average at least. So I devised an algorithm based on HSL color model, which treats the image more like a human eye.

Using the Code

The code for this article is pretty simple, and easy to understand. It consists of one interface IColorQuantizer, which provides a basic quantizer functionality. And one implementation class PaletteQuantizer, about which this article is.

Color Quantization Explained

It is a process that tries to reduce the number of colors in a given image to a certain limited number (given by the external factors), while keeping a visual essence of that image intact. It's usually used to satisfy display capabilities of certain devices, to reduce a raw size of the image. Also some image formats only support up-to the 256 colors (such as the GIF format). The color counts in a source image are usually much higher than that of those allowed, so the algorithm has to discard the colors carefully.

The Interface

I've tried to keep it as simple as possible, while allowing for other implementations to be integrated. Such as those octree based algorithms flying around here somewhere on Code Project. Because in my humble opinion, a good API is a first step. The comments are stripped away here, so all the methods can be described below in a greater detail. But at first look, I think you should already know what's coming.

public interface IColorQuantizer
{
    Boolean AllowParallel { get; } // introduced in version 5.0
    void Prepare(ImageBuffer image); // introduced in version 4.0 - changed in version 5.0
    void AddColor(Color color, Int32 x, Int32 y); // changed in version 5.0
    List<Color> GetPalette(Int32 colorCount);
    Int32 GetPaletteIndex(Color color, Int32 x, Int32 y); // changed in version 5.0
    Int32 GetColorCount();
    void Finish(); // introduced in version 5.0
    void Clear(); // deprecated in version 4.0
}

The Greater Detail

So let's take it one by one; no delays. The AddColor() method is used to feed the quantizer with the image pixel colors. To be later thrown away, and kept at palette range as needed. The basic idea is that you usually traverse all the pixels of one or more images (if you want to share that palette among them). All those colors are fed to the quantizer, which depending on the implementation will create various structures, and other contraptions, to spit a palette of a certain size at any moment. This method is the primary method, and will be used plentiful. So it should be as quick as possible.

Another important method is GetPalette(), which is usually the major know-how. There're many algorithms available, but basically it's all about squeezing out the representative points from the n-dimensional data (a cube in case of the RGB color model). Ideally the number of colors in a quantizer (i.e. a source image) is lower or equal to what we want. But it usually isn't the case. So instead of having all the true-colors, we're pushed to have only a limited set of those. And this method does exactly that. It picks a group of colors, and hopes that in the end, those will be the ones that represent the image most closely.

When we've our colors gathered, and a palette is determined, it's time to convert all the pixels from a truecolor (RGB or ARGB) to an index in our palette. As this method is also used on each pixel, it has to be also as fast as possible. Usually all the dirty tricks are used here. Basically you have an arbitrary color (up to 2^24 colors for RGB, or 2^32 colors for ARGB) for each pixel, and your mission - in this method - is to find that color in your mere (tops 256 colors) palette, and return its index. It's tough, but by far not impossible.

The last two methods, the GetColorCount(), and the Clear() are just cosmetic in comparison. The GetColorCount as its title indicates retrieves a number of unique colors currently stored in the quantizer. It's usually used to impress the users by what factor you reduced the color count, and it still looks the same.. well almost. The Clear() method is used as a maintenance method, to clear all the those precious colors. The new Prepare() method does what old Clear() did, but it also provides the chance to process the image beforehand (since version 4.0). A quantizer is then ready for another round, for another image.

In version 5.0 the method Finish() was added, to basically reintroduce the old Clear() method (but cowardly give it a different name so it seems like entirely different method). It is used to clean-up after the round since multiple quantizers were holding large amounts of memory when used simultanously. Also property AllowParallel to determine whether the quantizer supports parallel processing or not. Also somewhat notably the ImageBuffer class was refactored to clean-up and optimize the pixel processing.

My Way

Now that we know what methods are in the game, I won't be describing them one by one as I did implement them. I'll try to put together a meta-comment-bullet point-code of what is happening during those three phases.

Phase One - The Hash Table Cheat

Remember that this phase corresponds to reading all the pixels' color data, into our clever structure. My clever structure is a hash table. A simple Dictionary<Int32, Int32>, where key is the 32-bit color value (as in ARGB quad), and the value is number of the pixels of this color present in our image data. That presence counter doesn't play as big a role here so I call it a cheat, because a Boolean would do almost the same job here. But in the end, I've found some use for it.. soo that's that. MBC (meta-bullet-code):

• Scan through all the pixels of the source image.
• If a color is in the hashtable, increase the pixel presence value by 1.
• If it's not, add it and set the pixel presence to 1.

So far so good, but the most weird is still to come.

Phase Two - The Color Grinder

We now have all the pixels accounted for. So let the massacre begin. I'm talking about GetPalette() method here.

• Randomize (by a fixed seed of your choice) an order of the colors, the statistics is on our side.
• If there're less or equal colors in the quantizer than requested, we're done. Let's just take all of them. This is an ideal situation.
• Otherwise make three lists. One distinctly filtered by a hue, another by saturation, and the last one by brightness. Remember that those have to be the float representations.
• Determine which one of those has the most elements in it. A scanned image has the details in that area. Our candidates are in this one.

Let me explain here a bit before I continue. If a list with unique hues is the biggest, it's probably an image with many colors in it, so the importance will be to catch all those colorful details. If it's brightness, then there're probably some less colored, but highly shaded objects on the image. As for saturation, the details are mostly in the colored shades. So we're slightly adapting to what the eyes are seeing. Now that we have reduced a major part of the colors, let's begin to refine our choice a bit. Let's continue.

• If there are still more colors than we need, continue, otherwise we're done.
• Now make a similar death-match between the remaining aspects. If for example a hue was the major one, let's filter our colors again by brightness and saturation.
• Take again the one with more colors.
• If the winner has less colors than we need, just ignore it and rush to the last round.
• Otherwise, take those colors.
• As a last resort, try to filter out colors by the last aspect (if we choose a hue at 1^st level, and brightness at 2^nd level, be it saturation).
• And again, if this would result in less color than requested, ignore it.
• Otherwise pass it on.

At this point, we should have our colors really decimated at about the count we need, but if still there are too many colors, we'll simply do:

• Sort the remaining colors by the pixel count presence (our value in the hash).
• And just take the top (n) colors we've requested. Thus, we got exactly the count we needed.
• This is our result set of representative colors. So pass them out of the function.

Phase Three - Almost Euclidean

If you've followed all the steps here, you should now have a palette with pretty good color representation. Now all that is needed is to change all the colors on the target image to the indexes in our palette. You can use any algorithm you want, but I just used the good old Euclidean distance (without the square root, to speed it up).

• For each pixel in the source, take its color.
• Call the GetPaletteIndex() method.
• If a cache contains this color (we already asked for it before), return the cached index.
• Otherwise find it with Euclidean distance, and store the index in the cache. (Dictionary<Color, Byte>)
• Store the result index in the target image.

A Picture Is Worth A Thousand Words

I've found the courage to put all that in the diagram below, so feel free to check it out, and be forgiving. Some of my friends told me, that it's actually more confusing than just plain bullet points. But the effort was made, and perhaps some of you will like it better this way. So without further ado, here goes that monster.

Distinct Selection Quantizer (aka the color quantizer described in this article)

I've included this only as a comparison to other algorithms, I've tried to be objective.

	Very good image quality (especially photos) Supports all the color counts
	Memory consumption Slower  (in version 4.0 - can be improved by Locality-sensitive hash, or Octree search color caches)  (in version 5.0 - further improved by parallel processing, and other optimizations)

The Competit.. the Alternatives Out There

As pointed out by Som Shekhar, to list and briefly describe some other potential IColorQuantizer implementations out there. So here goes, as I promised.

Uniform Quantization (Included in version 2.0)

This algorithm is one of the oldest out there. It is sort of a naive approach. Each color component axis (red, green and blue) is divided into a few fixed segments (either 8-8-4 or 6-6-7 as in 255, resp. 252 colors). Each found color is placed into a corresponding segment slot. After all the colors are added, an average color is calculated for each slot. Those are the colors of the palette.

	Very quick Very small files Low on memory
	Bad image quality Only reduces to 256 colors

Popularity Algorithm (Included in Version 2.0)

Similar as the uniform quantization, and definitely from the same family, is a so called popularity algorithm. I was at first targeting to write something like this, but then it kind of evolved into something better (I hope). A RGB cube is also divided into little regions 4x4x4 (256/4 = 64 per color component, thus 262,144 little cubes). The colors are also placed into a corresponding region, and also the pixel presence is counted. After all the colors are in place, the top N regions with the highest pixel presence are chosen, an average color is calculated. Giving us N colors of the palette.

	Very small files Low on memory Supports all the color counts
	Very bad image quality for highly colored images

Median Cut (Included in Version 2.0)

The median cut took kind of different approach, and is more geometric in the nature. First it puts all the pixels out in the RGB space, then it finds the smallest box to enclose all of them (the worst cast scenario is a whole cube, but it's unusual). Then the iterative process begins. The longest axis is chosen (R, G or B) and the points are sorted along that axis. Then a median is calculated and the box is cut with a plane at that point. Thus we have two smaller boxes. For which we apply this recursively again and again until we got our N of boxes, whose contained colors are again averaged to give us the palette entries.

	Acceptable image quality Supports all the color counts
	Memory consumption Slower  (in version 4.0 - can be improved by Locality-sensitive hash, or Octree search color caches)  (in version 5.0 - further improved by parallel processing, and other optimizations)

Octree Algorithm (Included in Version 2.0)

There are plenty of articles around the web, as this is in current day the most used algorithm. Just to reference one here on The Code Project (CQuantizer). Basically, a cube is iteratively divided into the cubes (again). But this time, it's done along all the axis at once (Octree on Wikipedia). So the boxes are only created to cover the pixels inserted. Once all the colors are accounted for, the branches (those containing at least one leaf), are being reduced starting at the deepest level, because there the colors are usually nearer to each other. A branch is reduced by calculating an average value on all of its leaves, eliminating them and thus becoming a leaf itself. At the moment, we've lower or equal count of leaves as the colors we want, we stop reducing, and parse all the leaves for our palette colors. The reduction is therefore a destructive process, and octree can be used only once. Also up-to 8 leaves may be reduced at once, leaving us at the worst with 248 colors in the palette (which is not quite optimal).

	Very quick Good image quality
	Memory consumption Only 256 colors are supported  (in version 4.0 - support for any color count was added)

Spatial Color Quantization

I don't really know much about this method, as it's relatively new, and wasn't really eager to try it. All I know is it somehow combines quantization with dithering at the same time and is really exceptional for use to 16 colors or less. It's not that good for high color counts such as 256 colors. Check for yourself at SColorQ. Those were the images I tested against for lower bit rates. It's pretty impressive. I can't obviously compete against that dithering there at 4bpp and lower.

	Exceptionally good image quality
	Very slow Efficient only at 2-16 colors per palette Not good with photographs (and smooth images)

Wu's Color Quantizer (Included in Version 4.0)

Another geometrical quantizer is Wu's color quantizer by Xiaolin Wu. This algorithm is slower, but provides very good picture quality, unreachable by other algorithms. It's a clustering algorithm cuts the RGB space to find desired number of cubes. The parameter for cut being volume variance. As the author puts it: "Greedy orthogonal bipartition of RGB space for variance minimization aided by inclusion-exclusion tricks." I would recommend this algorithm, if quality is more important than speed for you.

	Exceptionally good image quality Supports all the color counts
	Slow Memory consumption

NeuQuant Algorithm (Included in Version 4.0)

This algorithm uses Kohonen Neural Network to learn the image colors. The neurons then correspond to the color slots, being optimized as the training of neural network proceeds. You can select between quality and speed. By sampling all the pixels, you'll achieve the maximal quality, or you can select lower quality (sampling step) to perform faster quantization. This algorithm should be used for higher color counts. I've limited it to 256 colors only. Feel free to experiment with other options. It performs better on visually rich images, such a the photos and rendered images.

	Good image quality (especially photos) - depends on the quality settings Memory consumption
	Slower - depends on the quality settings

Optimized Palette Algorithm (Included in Version 5.0)

Not much to say about this algorithm. It is basically a smart calculated (but unchangable) palette, that kinda covers all the colors, but none of them really. You'll get average results without need to synthetise a palette (as one is already ready), but the results will be also kinda average.

	Pretty fast Almost no memory consumption
	Very bad image quality Supports only 256 colors

Color Caches

Since version 4.0 the support for color caches was added. You can assign these IColorCache implementations via BaseColorQuantizer.ChangeColorCache(). This concept replaces 'me-being-lazy' default Euclidean distance nearest color search by introducing new interface:

public interface IColorCache
{
    void Prepare();
    void CachePalette(IEnumerable<Color> palette);
    void GetColorPaletteIndex(Color color, out Int32 paletteIndex);
}

This interface allows you to implement the search for optimal color within the quantized palette separately. The CachePalette() allows you to store already calculated palette in your clever structure. The GetColorPaletteIndex() replaces the IColorQuantizer's method (see for more details). The Prepare() method just removes all the clutter before first (or next) pass. There are three implementations available now.

Euclidean Distance

This is a standard three dimensional distance, but without a square root to speed things up. See Euclidean distance for more details. Below is a general equation for three dimensions:

Locality-Sensitive Hashing

I've searched the Internet to find some faster algorithms for a color matching. I've found this interesting general algorithm Nearest neighbor problem, and I've wondered if it could be of any use to me. Then I forged it into a functional version for color matching problem. So now you supply the 'quality' (number of buckets really). This algorithm can be further improved (speed) by combining more reference points (for example distance from white, and from red). The intersection can be then calculated to make more precise guess on nearest color, without the need to calculate expensive Euclidean distance. The quality ranges from 1 being best quality (+ overhead). This is not recommended as it brings no advantage. Other values: 8 (fast/quality 95%), 16 (faster/quality 85%), 32 (very quick/60%), or 64 (almost instant/30%). I would not go any further than that.

Octree Search

This technique combines the quick search in an octree algorithm with a specific palette of quantization algorithms without the need to use octree algorithm. It's considerably faster then Euclidean distance algorithm, without almost no quality impairment. This crude drawing below is a slightly modified version of Microsoft's crude drawing of full octree quantization algorithm. Each color in a palette is added to a list on each tree node it passes. When searching for a specific color. You'll find the most far node available, and then you perform comparison via Euclidean distance on all the colors in a list on a specific node.

Dithering

The dithering process is based on the fact, that human eye detects changes in the brightness more sensitively. So there is a need to reduce the effects of quantization on smoothness of final image brightness, but while still trying to keep its features (such as the edges, those are supposed to be sharp transition of brightness).

In version 5.0 a new interface was introduce to handle the dithering functionality. So let's briefly check out what it contains. The main method is ProcessPixel which takes a source pixel, performs a dithering routine on it's color, and then returns a dithered (target) pixel. Then there is a flag property IsInplace, this flag determines whether the dithering processing occurs on processed pixel only. Therefore the pixel can be process within the quantization pass (much faster). Method Prepare() serves to prepare the ditherer before the processing, and Finish() to clean-up after.

public interface IColorDitherer
{
    Boolean IsInplace { get; }
    void Prepare(IColorQuantizer quantizer, Int32 colorCount, ImageBuffer sourceBuffer, ImageBuffer targetBuffer);
    Boolean ProcessPixel(Pixel sourcePixel, Pixel targetPixel);
    void Finish();
}

There many methods for dithering, a brief list of some of the dithering methods included in this article are:

Ordered dithering

This type of dithering only processes the actual pixel without knowledge other changes in image (by dithering other pixels). This somewhat limits the ability, but still this methods produces image we're used to.

Read more on Wikipedia: Ordered dithering

Original	Bayer	Clustered-dot

Error-diffusion dithering

This method processes the pixels, and ditributes the accumulated error (difference) onto its neighbours. It depends on the order in which the pixels are processed.

Read more on Wikipedia: Error diffusion

Original	Floyd-Steinberg	Aktinson	Jarvis-Judice-Ninke

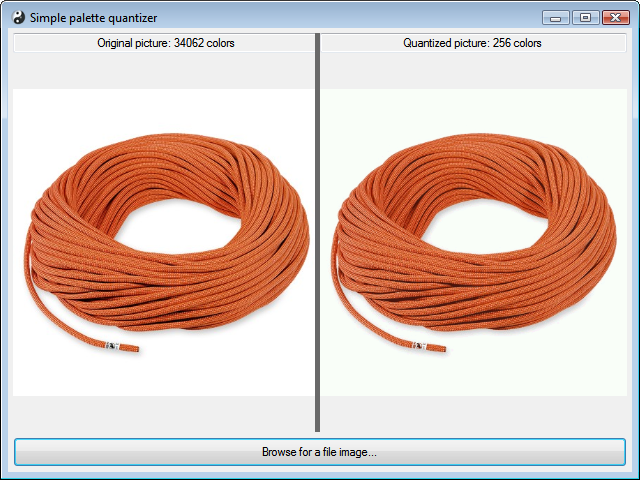
Screenshots Gallery

These are just few images to show the new capabilities of the utility inside, and also some new statistics.
You can now choose one from five methods of color quantization to compare the algorithms. Also you may select a bit-depth to which the source image will be reduced.

There's another selection on the left side, which allow you to preview the source image as it'd look like when saved as a GIF (especially for Roey C), and some projected size statistics, how big would the quantized image be when saved as a GIF or PNG.

In version 4.0, some new selections were added. First, you can now choose for some quantizers a type of color-cache to be used. In previous versions, only a slow Euclidean distance method was available. Now you can choose from two other faster methods.

Also in version 4.0, support for color models for some color caches was added. It doesn't make much more difference, but it's there to be further optimized (I'm lazy). I added the support, then I noticed that it doesn't really make a difference, but I left it there.

Version 5.0 brought the support for parallel processing which really takes advantage of multi-core processors, and allows to use full speed potential.

The Version 5.0 also contains a support for dithering. This can lead to potential improvement of color reduction quality (it can also lead to worse quality though).

Feedback

Feel free to ask anything in the forum below, as usual. I'm working on some bigger projects at the moment, so I'll be posting another article really soon. This quantizer will probably be a part of it, even though a non-essential part.

Related Articles

• Image per pixel enumeration, pixel format conversion and more

Change Log

Version 5.0

• New alogrithm included: Optimal Palette Quantizer (ok it's a kinda cheating, but I wanted to add some new method).
• All the graphics routines are rewritten, and optimized. Now contains direct pixel (regardless the depth) access.
• Support for parallel processing was added. This leads to a speed-up (depends on processor core count).
• Because dithering methods were metioned few times in comment section. Few dithering methods are now added.
• Faster random numbers (credit goes to colgreen), because speed matters here, randomness not as much.
• Other general speed-ups like early palette detection (less than needed colors), avoiding floats, Color (24 bytes!) when possible.
• Color count detection fixed for all the methods.

Version 4.0

• Two new algorithms included: Wu's Color Quantizer, and NeuQuant neural network based quantizer
• General optimization profiling speed-up about 2x the original speed
• The pixel enumeration now supports in-memory version, this should bring some speed up in some cases
• Some quantizers now support an interchangeable color cache. Speed-up is about 2-3x (up-to 5-6x in some cases)
• Repaired fatal flaw in processing indexed images (Image.Palette!), this increases speed for indexed images up-to 100x
• New color cache concept, to allow for faster then slow Euclidean nearest color
• Some color caches also include option for color models
• The utility can now load and process all the pixel formats (even indexed ones)
• The utility now displays image filename when opened
• Note: Testing image 3072 x 2304 (169220 colors) now takes 3.5s (with HSL method + Octree search) on my CPU
• Note: Image 512 x 512 (155774 colors) takes 0.5s. So it scales well with size. Basically Dictionary (C#) speed issue from now on
• Note: Don't forget to test outside Visual Studio, and built in Release mode

Version 3.0

• The Octree quantizer now supports all the color counts (as requested by Matt Perdeck)
• Quantized image is now stored in an optimal pixel format (auto-detection)
• NRMSD (normalized root-mean-square deviation) can now be calculated
• Few minor fixes, and speedups

Version 2.0

• Various speed optimizations (thanks to Andrew Rissing)
• Support for alpha-blending included
• Many quantization algorithms included
• Support for semi-transparent images added
• Projected statistics added (for Roey C)
• Quantization process duration is now measured
• Code comments coverage increased
• Interface slightly changed, to support more palette indexes (Andrew Rissing)

Version 1.0

• Initial spontaneous version released

History

• 2012-07-28: Version 5.0 published
• 2011-07-04: The section Color caches added
• 2011-07-04: Version 4.0 published
• 2011-07-02: Version 3.0 published
• 2010-03-26: Version 2.0 published
• 2010-03-19: The section Color quantization explained added
• 2010-03-18: The section The competit.. the alternatives out there added
• 2010-03-18: The initial article was posted