Introduction
The purpose of this post is to describe a Crossword generation web application and its associated progressive search algorithm.
The reader can browse the English version or the Arabic version.
Progressive search is a randomized iterative search algorithm that the author has developed and found to be effective for a variety of optimization problems; more information on this can be found at my activities page and my book on algorithms, Algorithms: Development and Programming.
Crossword puzzles are popular word games that serve to challenge, entertain and
educate. Crossword puzzles owe their popularity to their being a stable feature
in almost every newspaper worldwide. Educators have also found crossword puzzles
an effective means for measuring a person’s knowledge on a particular subject.
In its basic form, the crossword generation problem is stated as follows:
Given a rectangular (or square) grid of certain dimensions and a word list (lexicon),
produce a set of horizontal words and a set of vertical words along with their row
and column locations (cells) for filling of the empty cells. For unconstrained crossword, the algorithm is to determine the positions
of the black cells — some of which are needed to separate adjacent words. For constrained crossword, the positions of black cells are fixed at the start.
The algorithm presented here is for unconstrained crosswords (that is, it includes sub-algorithms for determining black cells as explained later). The crossword generation problem is different from (and seems easier than) crossword solving problem. The latter problem calls for finding word answers consistent with the given clues.
Crosswords puzzles can be about numbers too. Using a programmatically generated lexicon of numbers (i.e., for a number z=x*y, z is a word and x*y is a word definition), it is possible to produce a crossword puzzle of grid size = 10 with about 40 interrelated multiplication problems that can serve as an exercise for students in the third grade. Our Crossword application generates such crosswords using the Numeric option (see above figure).
In this article, we explain our progressive-search algorithm for generating crosswords
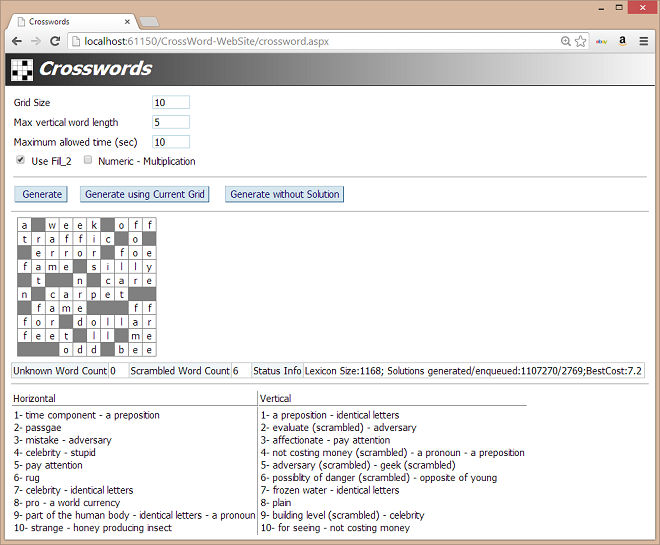
and its encapsulation into a program component (a class library that can be compiled into a DLL), along with its web-based application. The above figure shows the basic structure of the interface and a sample crossword
generated by the component.
How to use the Crossword component
To create a crossword, as illustrated by the following ASPX script, create an instance of
the Crossword class, set its attributes (DBPath, GridSize, ... etc.) and call
CreateCrossword().
<%@ Language="C#" debug="true" %>
<html>
<head>
<title>Test Component</title>
<style type="text/css" >
td.cwcell { width:16px; text-align:center; background-color:white; }
td.cwstar { width:16px; text-align:center; background-color:gray; color:white; }
td { font-family:Tahoma; font-size: 10pt; }
</style>
</head>
<%
Crossword cw = new Crossword();
cw.DBPath=Server.MapPath("") + @"\crossword_dbs\crossword.mdb";
cw.TimeToStop = 2;
cw.GridSize = 12;
cw.VPlacement = true;
cw.MaxVWordLength = 4;
cw.QMAXSIZE = 40;
cw.NBSIZE = 50;
string msg = cw.CreateCrossWord(null);
msg = "<table border='0' cellspacing='1' bgcolor='gray'>" + cw.BestSolution.PrintGrid() + "</table>";
string msg3 =cw.BestSolution.GetVWordList();
msg3 ="<table border='0' cellspacing='1' cellpadding='0' >" + msg3 + "</table>";
int invalidcount = cw.BestSolution.InvalidWordCount;
int scrambledcount = cw.BestSolution.ScrambledWordCount;
%>
<body>
<p><b> Unknown Words= <% =invalidcount %> Scrambled Words = <% =scrambledcount %></b>
</p>
<hr/>
<table>
<tr><td><% =msg %></td><td><b>Vertical Words</b><br/><% =msg3 %></td></tr>
</table>
</body>
</html>
The preceding script (when accessed by browser) produces an output similar to the following screen capture.

Crossword Generation using Progressive Search
The proposed crossword generation algorithm starts by filling the grid with horizontal words
and then computes a cost-measure of this solution — for example, the number of unknown
(not found in the lexicon) vertical words — which represents the objective function to be minimized. Then as a mutation of the current solution, the algorithm chooses a horizontal word and replaces it by a randomly-selected lexicon word of the same length. Using this kind of mutation guarantees that all solutions generated during the progress toward the final solution, have valid horizontal words; hence, the cost of a solution can be computed by scanning the grid columns and counting unknown or scrambled words. The coupling of this idea to progressive search can be outlines as follows.
- Generate an initial solution X, through horizontal fill and compute its measure of goodness, f(X) as some expression related to the number of unknown or scrambled words in the vertical view. Save X as the current best solution and enqueue X.
- Progressive Search: Repeatedly dequeue (or choose one at a random) a solution S,
generate a neighborhood of solutions from S by mutation and enqueue those solutions
whose cost fall within some preset threshold. Terminate if an optimal solution is found
(i.e., cost = 0) or the elapsed time has exceeded some preset time-period.
As explained in the author’s Sudoku article, we will use an implementation of progressive search where the items are enqueued by negative of cost to avoid threshold calculation.
The Crossword component consists of two classes: Crossword class that handles input and output (including the loading of a lexicon from a specified database), and Solution class that encodes any solution generated during the exploration of the search space. The
Solution class is subordinate to the Crossword class. To facilitate access to members defined in the
Crossword class, the Solution class include a member cw that points to this instance of the
Crossword class.
The following listing shows parts of the program code for the Crossword class.
public string CreateCrossWord(Solution s1)
{
if (Numeric)
{ MaxWordLength = GenWords(ref WordList, ref WordDescList);
FreqChar = new char[] { '1', '2', '3', '4', '5', '6', '7', '8', '9' };
MinWordLength = 2;
goto cont;
}
if (Arabic)
FreqChar = new char[] { 'ع', 'ب', 'ت', 'ي', 'ن', 'م', 'ل', 'و' };
else FreqChar = new char[] { 'e', 'r', 'a', 'i', 'n', 't', 'o', 's' };
if (s1 != null)
{ this.WordList = s1.cw.WordList;
this.WordDescList = s1.cw.WordDescList;
this.WordSigList = s1.cw.WordSigList;
this.MaxWordLength = s1.cw.MaxWordLength;
goto cont;
}
MaxWordLength = GetLexicon(DBPath, ref WordList, ref WordDescList, ref WordSigList);
int max = MaxWordLength;
if (GridSize < MaxWordLength) max = GridSize;
for (int i = MinWordLength; i <= max; i++)
if (WordList[i].Count == 0)
return "Maximum Word Length:" + MaxWordLength + " Supply Words of Length:" + i;
cont:
if (s1 == null) s1 = new Solution(this, false);
if (TimeToStop == -1) return ComputeFillMeasure();
if (TimeToStop == 0)
{ BestSolution = s1;
StatusInfo = "";
}
else BestSolution = ProgressiveSearch(s1);
return "";
}
The following listing shows parts of the program code for the Solution class. The basic information here is that any filling of the crossword grid represents a solution (node) in our search space.
Thus, a solution is completely characterized by its filled grid or, alternatively, its
ItemList (a list of horizontal words and their respective locations). However, for clarity and to speed up the process of mutation, we have chosen to keep both structures, which is evident from the initial lines of the following partial listing of the Solution class:
struct SolutionItem
{ internal int row, col;
internal string word;
internal SolutionItem(int r, int c, string w)
{ row = r; col = c; word = w; }
}
public class Solution
{ internal Crossword cw;
Random rand;
internal char[,] grid;
internal int GridSize;
ArrayList ItemList = new ArrayList();
public float Cost;
public int InvalidWordCount, ScrambledWordCount;
public Solution(Crossword cw, bool empty)
{
this.cw = cw;
GridSize = cw.GridSize;
this.rand = cw.rand;
if (empty) return;
grid = new char[GridSize, GridSize];
if (cw.VPlacement || (cw.MaxVWordLength == -1))
Fill_2();
else Fill_1();
Cost = ComputeMeasure();
}
void PlaceWord(string wrd, int row, int col)
{ if (wrd.Length == 1)
{ grid[row, col] = wrd[0]; return; }
SolutionItem it = new SolutionItem(row, col, wrd);
ItemList.Add(it);
if (cw.Arabic)
for (int i = col; i < wrd.Length; i++)
{ grid[row, col+i] = wrd[wrd.Length - 1 - i]; }
else
for (int i = col; i < wrd.Length; i++)
{ grid[row, col+i] = wrd[i]; }
}
}
Most of the methods in the Solution class are language neutral. The method PlaceWord() (shown above) is language dependent. The function modifies a solution by placing a word (specified as wrd parameter) horizontally at the location specified by the row and col parameters.
A key method in the Solution class is NewSolution(), which is defined by the following:
internal Solution NewSolution()
{ Solution s1 = this.CopySolution();
int r = rand.Next(ItemList.Count);
SolutionItem it = (SolutionItem) ItemList[r];
string wrd = cw.GetWord(it.word.Length);
s1.PlaceWord(wrd, it.row, it.col);
foreach (SolutionItem itx in ItemList)
if ( (itx.row!=it.row) || (itx.col!=it.col))
s1.ItemList.Add(new SolutionItem(itx.row,itx.col,itx.word));
s1.ComputeMeasure();
return s1;
}
This works as follows. We have to mutate a solution S into a new solution
S1.
We begin by having S1 as a copy of S. Then we randomly pick a horizontal word w from the grid (equivalent to picking an item it from ItemList).
We then select a random lexicon word wrd and have it replace the word
w.
This last action is reflected in the grid of S1 via the call to PlaceWord(). We then use the foreach loop a build the ItemList of S1.
Finally, we issue the call ComputeMeasure() to compute and set the cost of
S1.
What Objective Function to Use?
This is concerning the expression used by ComputeMeasure() for the solution's cost (i.e.,how far it is from an optimal (with cost=0) solution).
Given a solution S to a crossword puzzle, let u denote the
number of unknown vertical words and w denote the number
of scrambled vertical words. As a simple cost function for a solution S,
we define f(S) = u. However, such a function causes
termination when the number unknown vertical words reaches zero, yet there may
be plenty of scrambled vertical words, which is generally undesirable. To
account for scrambled words, the expression f(S) = u+0.5*w
is a better choice (unknown words have twice the weight of scrambled words).
Further reflection reveals that such a function does not distinguish among solutions that have the same number of unknown and scrambled words but where the length of such words vary sharply for different solutions. Intuition suggests that by moving along the direction that reduces
the length of unknown words [scrambled words], we eventually reduce the number of unknown words [scrambled words].
Thus, a better expression for f(S) = len(u)
+ 0.2*len(w), where len(u) is the combined length of unknown vertical words and len(w) is the combined length
of scrambled vertical words (Note: we have found that a factor of 0.2 works better than 0.5).
Filling Strategies
A basic strategy for the filling (determining the positions of black cells) of a grid is the following:
process the grid row-wise, and for each row place randomly chosen words.
However, there are few problems that must be addressed. First, we like to have
the possibility of having word slots of length one as well as the possibility of
a leftmost (or a rightmost) cell in any row be black.
This suggests that the determination of word slots (equivalently word lengths)
be based on generating random numbers between zero and maximum word length
MaxWordLength (as determined from input lexicon) inclusive, where a word length
of zero means that the current cell, that will be normally the start of a word,
will be blackened. A word of length one is selected at random from the set of
the eight most frequent English letters. Such a strategy has still one minor
problem relating to the vertical view; a column may end up having many adjacent white cells,
making it difficult to match with a 9-letter word later for instance.
To address this problem, and to vary the density of black cells, the filling strategy
is augmented with a parameter MaximumVWordLength (the maximum length
for any vertical word).
The implementation of this strategy is shown as Fill_1() method in the following listing.
void Fill_1()
{ int k, wlen, remlen; int[] cc = new int[GridSize];
for (int i = 0; i < GridSize; i++)
{ cc[i] = 0;
for (int j = 0; j < GridSize; j++)
{ grid[i, j] = '*'; }
}
for (int i = 0; i < GridSize; i++)
{ int j = 0;
while (j < GridSize)
{ remlen = GridSize - j;
if (remlen > cw.MaxWordLength) remlen = cw.MaxWordLength;
if (remlen > 3)
wlen = rand.Next(remlen + 1);
else wlen = remlen;
for (k = j; k < j + wlen; k++)
{ if (cc[k] >= cw.MaxVWordLength) break;
cc[k]++;
}
wlen = k - j;
if (k < GridSize) cc[k] = 0;
if (wlen > 0) PlaceWord(cw.GetWord(wlen), i, j);
j = j + wlen + 1;
}
}
}
We utilize a vector cc[0..GridSize-1], where cc[k] is the
count of white cells for column k. Also, note that, first, the word length wlen is
chosen as a random number between zero and minimum of (MaxWordLength,
remlen), where remlen is the number of remaining unfilled cells in the current row. If
remlen is ≤ 3 then wlen is reset to remlen.
Then wlen is further reduced to ensure that cc[k] ≤ MaxVWordLength for the columns spanned by the current word.
An alternative filling strategy is given by Fill_2() method in the following listing.
void Fill_2()
{
for (int i = 0; i < GridSize; i++)
for (int j = 0; j < GridSize; j++)
{ grid[i, j] = 'X'; }
for (int col = 0; col < GridSize; col++)
{ int row = 0;
while (row < GridSize)
{
int wlen = rand.Next(cw.MaxVWordLength + 1);
row = row + wlen;
if (row >= GridSize) break;
if ((row > 0) && (grid[row - 1, col] == '*')) continue;
grid[row, col] = '*';
}
}
for (int i = 0; i < GridSize; i++)
{ int wlen = 0; int startpos = 0;
for (int j = 0; j <= GridSize; j++)
{ if (j == GridSize)
{ if (wlen > 0) PlaceWord(cw.GetWord(wlen), i, startpos);
break;
}
if ((grid[i, j] == 'X') && (wlen < cw.MaxWordLength)) wlen++;
else
{ if (wlen > 0) PlaceWord(cw.GetWord(wlen), i, startpos);
grid[i, j] = '*';
wlen = 0;
startpos = j + 1;
}
}
}
}
In this strategy, the black cells are chosen based on a vertical view, by processing
the grid column-wise and generating random word lengths (up to MaximumVWordLength).
The grid is then processed row-wise for the purpose of horizontal word filling.
Conclusions
Crossword generation is a good example demonstrating the effectiveness of progressive search.
This application was tested with popular browsers and found to work properly.
History
- 4th December, 2013: Version 1.0.
