Preface
This article is a repost of an original from my former blog on thousand-thoughts.com which has been discontinued. The request for this article were so high, that I decided to save it here on Code Project. The original article has been posted 16th March 2012, so it uses a dated Android API. However, the approach could still be an interesting topic. Since then the code has been put into use by several developers. Jose Collas created a more user komfortable framework from the original code and put it into a github repository.
Introduction
While working on my master thesis, I’ve made some experiences with sensors in Android devices and I thought I’d share them with other Android developers. In my work I was developing a head tracking component for a prototype system. Since it had to adapt audio output to the orientation of the users head, it required to respond quickly being accurate at the same time.
I used my Samsung Galaxy S2 and decided to use its gyroscope in conjunction with the accelerometer and the magnetic field sensor in order to measure the user’s head rotations both, quickly and accurately. To acheive this I implemented a complementary filter to get rid of the gyro drift and the signal noise of the accelerometer and magnetometer. The following tutorial describes in detail how it’s done.
This tutorial is based on the Android API version 10 (platform 2.3.3).
This article is divided into two parts. The first part covers the theoretical background of a complementary filter for sensor signals as described by Shane Colton from MIT here. The second part describes the implementation in the Java programming laguage. Everybody who thinks the theory is boring and wants to start programing right away can skip directly to the second part.
Sensor Fusion via Complementary Filter
The common way to get the attitude of an Android device is to use the SensorManager.getOrientation() method to get the three orientation angles. These two angles are based on the accelerometer and magenotmeter output. In simple terms, the acceletometer provides the gravitiy vector (the vector pointing towards the centre of the earth) and the magnetometer works as a compass. The Information from both sensors suffice to calculate the device’s orientation. However both sensor outputs are inacurate, especially the output from the magnetic field sensor which includes a lot of noise.
The gyroscope in the device is far more accurate and has a very short response time. Its downside is the dreaded gyro drift. The gyro provides the angular rotation speeds for all three axes. To get the actual orientation those speed values need to be integrated over time. This is done by multiplying the angular speeds with the time interval between the last and the current sensor output. This yields a rotation increment. The sum of all rotation increments yields the absolut orientation of the device. During this process small errors are introduced in each iteration. These small errors add up over time resulting in a constant slow rotation of the calculated orientation, the gyro drift.
To avoid both, gyro drift and noisy orientation, the gyroscope output is applied only for orientation changes in short time intervals, while the magnetometer/acceletometer data is used as support information over long periods of time. This is equivalent to low-pass filtering of the accelerometer and magnetic field sensor signals and high-pass filtering of the gyroscope signals. The overall sensor fusion and filtering looks like this:
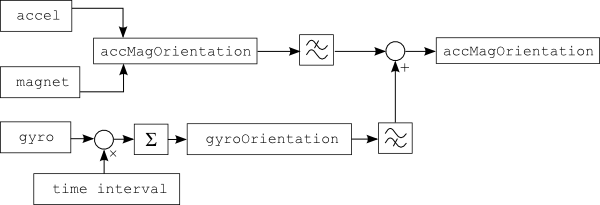
So what exactly does high-pass and low-pass filtering of the sensor data mean? The sensors provide their data at (more or less) regular time intervals. Their values can be shown as signals in a graph with the time as the x-axis, similar to an audio signal. The low-pass filtering of the noisy accelerometer/magnetometer signal (accMagOrientation in the above figure) are orientation angles averaged over time within a constant time window.
Later in the implementation, this is accomplished by slowly introducing new values from the accelerometer/magnetometer to the absolute orientation:
accMagOrientation = ( 1 - factor ) * accMagOrientation+ factor * newAccMagValue;
The high-pass filtering of the integrated gyroscope data is done by replacing the filtered high-frequency component from accMagOrientation with the corresponding gyroscope orientation values:
fusedOrientation =
(1 - factor) * newGyroValue
+ factor * newAccMagValue;
In fact, this is already our finished comlementary filter.
Assuming that the device is turned 90° in one direction and after a short time turned back to its initial position, the intermediate signals in the filtering process would look something like this:

Notice the gyro drift in the integrated gyroscope signal. It results from the small irregularities in the original angular speed. Those little deviations add up during the integration and cause an additional undesireable slow rotation of the gyroscope based orientation.
Implementation
Now let’s get started with the implementation in an actual Android application.
Setup and Initialization
First we need to set up our Android app with the required members, get the SensorManager and initiaise our sensor listeners, for example, in the onCreate method:
public class SensorFusionActivity extends Activity implements SensorEventListener{
private SensorManager mSensorManager = null;
private float[] gyro = new float[3];
private float[] gyroMatrix = new float[9];
private float[] gyroOrientation = new float[3];
private float[] magnet = new float[3];
private float[] accel = new float[3];
private float[] accMagOrientation = new float[3];
private float[] fusedOrientation = new float[3];
private float[] rotationMatrix = new float[9];
public void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
setContentView(R.layout.main);
gyroOrientation[0] = 0.0f;
gyroOrientation[1] = 0.0f;
gyroOrientation[2] = 0.0f;
gyroMatrix[0] = 1.0f; gyroMatrix[1] = 0.0f; gyroMatrix[2] = 0.0f;
gyroMatrix[3] = 0.0f; gyroMatrix[4] = 1.0f; gyroMatrix[5] = 0.0f;
gyroMatrix[6] = 0.0f; gyroMatrix[7] = 0.0f; gyroMatrix[8] = 1.0f;
mSensorManager = (SensorManager) this.getSystemService(SENSOR_SERVICE);
initListeners();
}
} Notice that the application implements the <code>SensorEventListener interface. So we’ll have to implement the two methods onAccuracyChanged and onSensorChanged. I’ll leave onAccuracyChanged empty since it is not necessary for this tutorial. The more important function is onSensorChanged. It updates our sensor data continuously.
The initialisation of the sensor listeners happens in the initListeners method:
public void initListeners(){
mSensorManager.registerListener(this,
mSensorManager.getDefaultSensor(Sensor.TYPE_ACCELEROMETER),
SensorManager.SENSOR_DELAY_FASTEST);
mSensorManager.registerListener(this,
mSensorManager.getDefaultSensor(Sensor.TYPE_GYROSCOPE),
SensorManager.SENSOR_DELAY_FASTEST);
mSensorManager.registerListener(this,
mSensorManager.getDefaultSensor(Sensor.TYPE_MAGNETIC_FIELD),
SensorManager.SENSOR_DELAY_FASTEST);
} Acquiring and Processing Sensor Data
After the listeners are initialised, the onSensorChanged method is called automatically whenever new sensor data is available. The data is then copied or processed, respectively.
public void onSensorChanged(SensorEvent event) {
switch(event.sensor.getType()) {
case Sensor.TYPE_ACCELEROMETER:
System.arraycopy(event.values, 0, accel, 0, 3);
calculateAccMagOrientation();
break;
case Sensor.TYPE_GYROSCOPE:
gyroFunction(event);
break;
case Sensor.TYPE_MAGNETIC_FIELD:
System.arraycopy(event.values, 0, magnet, 0, 3);
break;
}
}The Android API provides us with very handy functions to get the absolute orientation from the accelerometer and magnetometer. This is all we need to do to get the accelerometer/magnetometer based orientaion:
public void calculateAccMagOrientation() {
if(SensorManager.getRotationMatrix(rotationMatrix, null, accel, magnet)) {
SensorManager.getOrientation(rotationMatrix, accMagOrientation);
}
}As described above, the gyroscope data requires some additional processing. The Android reference page shows how to get a rotation vector from the gyroscope data (see Sensor.TYPE_GYROSCOPE
public static final float EPSILON = 0.000000001f;
private void getRotationVectorFromGyro(float[] gyroValues,
float[] deltaRotationVector,
float timeFactor)
{
float[] normValues = new float[3];
float omegaMagnitude =
(float)Math.sqrt(gyroValues[0] * gyroValues[0] +
gyroValues[1] * gyroValues[1] +
gyroValues[2] * gyroValues[2]);
if(omegaMagnitude > EPSILON) {
normValues[0] = gyroValues[0] / omegaMagnitude;
normValues[1] = gyroValues[1] / omegaMagnitude;
normValues[2] = gyroValues[2] / omegaMagnitude;
}
float thetaOverTwo = omegaMagnitude * timeFactor;
float sinThetaOverTwo = (float)Math.sin(thetaOverTwo);
float cosThetaOverTwo = (float)Math.cos(thetaOverTwo);
deltaRotationVector[0] = sinThetaOverTwo * normValues[0];
deltaRotationVector[1] = sinThetaOverTwo * normValues[1];
deltaRotationVector[2] = sinThetaOverTwo * normValues[2];
deltaRotationVector[3] = cosThetaOverTwo;
} The above function creates a rotation vector which is similar to a quaternion. It expresses the rotation interval of the device between the last and the current gyroscope measurement. The rotation speed is multiplied with the time interval — here it’s the parameter timeFactor — which passed since the last measurement. this function is then called in the actual gyroFunction for gyro sensor data processing. This is where the gyroscope rotation intervals are added to the absolute gyro based orientation. But since we have rotation matrices instead of angles this can’t be done by simply adding the rotation intervals. We need to apply the rotation intervals by matrix multiplication:
private static final float NS2S = 1.0f / 1000000000.0f;
private float timestamp;
private boolean initState = true;
public void gyroFunction(SensorEvent event) {
if (accMagOrientation == null)
return;
if(initState) {
float[] initMatrix = new float[9];
initMatrix = getRotationMatrixFromOrientation(accMagOrientation);
float[] test = new float[3];
SensorManager.getOrientation(initMatrix, test);
gyroMatrix = matrixMultiplication(gyroMatrix, initMatrix);
initState = false;
}
float[] deltaVector = new float[4];
if(timestamp != 0) {
final float dT = (event.timestamp - timestamp) * NS2S;
System.arraycopy(event.values, 0, gyro, 0, 3);
getRotationVectorFromGyro(gyro, deltaVector, dT / 2.0f);
}
timestamp = event.timestamp;
float[] deltaMatrix = new float[9];
SensorManager.getRotationMatrixFromVector(deltaMatrix, deltaVector);
gyroMatrix = matrixMultiplication(gyroMatrix, deltaMatrix);
SensorManager.getOrientation(gyroMatrix, gyroOrientation);
} The gyroscope data is not processed until orientation angles from the accelerometer and magnetometer is available (in the member variable accMagOrientation). This data is required as the initial orientation for the gyroscope data. Otherwise, our orientation matrix will contain undefined values. The device’s current orientation and the calcuated gyro rotation vector are transformed into a rotation matrix.
The gyroMatrix is the total orientation calculated from all hitherto processed gyroscope measurements. The deltaMatrix holds the last rotation interval which needs to be applied to the gyroMatrix in the next step. This is done by multiplying gyroMatrix with deltaMatrix. This is equivalent to the Rotation of gyroMatrix about deltaMatrix. The matrixMultiplication method is described further below. Do not swap the two parameters of the matrix multiplication, since matrix multiplications are not commutative.
The rotation vector can be converted into a matrix by calling the conversion function getRotationMatrixFromVector from the SensoManager. In order to convert orientation angles into a rotation matrix, I’ve written my own conversion function:
private float[] getRotationMatrixFromOrientation(float[] o) {
float[] xM = new float[9];
float[] yM = new float[9];
float[] zM = new float[9];
float sinX = (float)Math.sin(o[1]);
float cosX = (float)Math.cos(o[1]);
float sinY = (float)Math.sin(o[2]);
float cosY = (float)Math.cos(o[2]);
float sinZ = (float)Math.sin(o[0]);
float cosZ = (float)Math.cos(o[0]);
xM[0] = 1.0f; xM[1] = 0.0f; xM[2] = 0.0f;
xM[3] = 0.0f; xM[4] = cosX; xM[5] = sinX;
xM[6] = 0.0f; xM[7] = -sinX; xM[8] = cosX;
yM[0] = cosY; yM[1] = 0.0f; yM[2] = sinY;
yM[3] = 0.0f; yM[4] = 1.0f; yM[5] = 0.0f;
yM[6] = -sinY; yM[7] = 0.0f; yM[8] = cosY;
zM[0] = cosZ; zM[1] = sinZ; zM[2] = 0.0f;
zM[3] = -sinZ; zM[4] = cosZ; zM[5] = 0.0f;
zM[6] = 0.0f; zM[7] = 0.0f; zM[8] = 1.0f;
float[] resultMatrix = matrixMultiplication(xM, yM);
resultMatrix = matrixMultiplication(zM, resultMatrix);
return resultMatrix;
}I have to admit, this function is not optimal and can be improved in terms of performance, but for this tutorial it will do the trick. It basically creates a rotation matrix for every axis and multiplies the matrices in the correct order (y, x, z in our case).
This is the function for the matrix multiplication:
private float[] matrixMultiplication(float[] A, float[] B) {
float[] result = new float[9];
result[0] = A[0] * B[0] + A[1] * B[3] + A[2] * B[6];
result[1] = A[0] * B[1] + A[1] * B[4] + A[2] * B[7];
result[2] = A[0] * B[2] + A[1] * B[5] + A[2] * B[8];
result[3] = A[3] * B[0] + A[4] * B[3] + A[5] * B[6];
result[4] = A[3] * B[1] + A[4] * B[4] + A[5] * B[7];
result[5] = A[3] * B[2] + A[4] * B[5] + A[5] * B[8];
result[6] = A[6] * B[0] + A[7] * B[3] + A[8] * B[6];
result[7] = A[6] * B[1] + A[7] * B[4] + A[8] * B[7];
result[8] = A[6] * B[2] + A[7] * B[5] + A[8] * B[8];
return result;
} The Complementary Filter
Last but not least we can implement the complementary filter. To have more control over its output, we execute the filtering in a separate timed thread. The quality of the sensor signal strongly depends on the sampling frequency, that is, how often the filter method is called per second. That’s why we put all the calculations in a TimerTask and define later the time interval between each call.
class calculateFusedOrientationTask extends TimerTask {
public void run() {
float oneMinusCoeff = 1.0f - FILTER_COEFFICIENT;
fusedOrientation[0] =
FILTER_COEFFICIENT * gyroOrientation[0]
+ oneMinusCoeff * accMagOrientation[0];
fusedOrientation[1] =
FILTER_COEFFICIENT * gyroOrientation[1]
+ oneMinusCoeff * accMagOrientation[1];
fusedOrientation[2] =
FILTER_COEFFICIENT * gyroOrientation[2]
+ oneMinusCoeff * accMagOrientation[2];
gyroMatrix = getRotationMatrixFromOrientation(fusedOrientation);
System.arraycopy(fusedOrientation, 0, gyroOrientation, 0, 3);
}
}If you’ve read the first part of the tutorial, this should look somehow familiar to you. However, there is one important modification. We overwrite the gyro based orientation and rotation matrix in each filter pass. This replaces the gyro orientation with the “improved” sensor data and eliminates the gyro drift.
Of course, the second important factor for the signal quality is the FILTER_COEFFICIENT. I’ve determined this value heuristically by rotating a 3D-model of my smartphone using the sensor from my actual device. A value of 0.98 with a sampling rate of 33Hz (this yields a time period of 30ms) worked quite well for me. You can increase the sampling rate to get a better time resolution, but then you have to adjust the FILTER_COEFFICIENT to improve the signal quality.
So these are the final additions to our sensor fusion code:
public static final int TIME_CONSTANT = 30;
public static final float FILTER_COEFFICIENT = 0.98f;
private Timer fuseTimer = new Timer();
public void onCreate(Bundle savedInstanceState) {
fuseTimer.scheduleAtFixedRate(new calculateFusedOrientationTask(),
1000, TIME_CONSTANT);
}I hope this tutorial could provide a sufficient explanation on custom sensor fusion on Android devices.
History
18th Feb 2014: Article reposted from original.
