Using Genetic Algorithm To Solve Perfect Matching Problem

• Download source - 347.1 KB
• Download demo - 102.7 KB

Table of Contents

1. Introduction
2. Background
3. Genetic Algorithm
1. How It Works
2. Genetic Operators
1. Crossing-Over
2. Mutation
3. Elite
4. Perfect Matching Problem
5. Fixture Generation Problem
6. Using the code
7. Conclusion
8. History

1. Introduction

Genetic algorithms are really useful to solve NP-Complete optimization problems. These problems usually have many different parameters that can vary simultaneously which makes working through every combination of all the parameters computationally very slow and not feasible. The basic idea is to start with a population of individuals and to allow that population to evolve to a more fit state.

2. Background

All terms & definitions are explained in wiki clearly, I won't retype them here. In my code sample, I used a framework called GAF (Genetic Algorithm Framework) which is written by John Newcombe. Thanks to him, I didn't deal with implementation details of genetic algorithm, he had done all of the hard work. He has a great blog about it, I strongly suggest you go and check.

• Genetic Algorithms in C#

To add the GAF to a project by NuGet;

PM> Install-Package GAF

And some words from that blog;

"Genetic Algorithms (GAs) are the nearest thing a software developer can get to magic. Watching a solution to a problem 'evolve', is awesome."

For more information about NP-Complete problems, please see this.

3. Genetic Algorithm

3.1 How It Works

Genetic algorithms are analogous to those in the natural world; survival of the fittest, or natural selection. It is an evolutionary approach to computing. Computationally, the process is very similar to the biological one. There are two critical steps that must be taken before a genetic algorithm can be run:

• Define a set of individuals that might represent a solution to the problem.
• Define a fitness function that can quantify how close an individual is to being a good answer.

Let's itemize the whole process:

• Create a randomly generated initial population at first. Random generation generates solution candidates (chromosomes) with allowing the entire range of possible solutions in the search space.
• Evaluate each solution candidate, sort by descending fitness values, and take a proportion of the existing population. The most-fit individuals will mate more often and some fraction of the least-fit individuals will be discarded.
• Use this set to breed a new generation and evaluate the set.
• Swap some of the existing solutions with some of the new ones and evaluate new solutions. The matings are used to generate new individuals who will replace those who died. This keeps the population at the same size in each generation.
• Previous step is performed till terminate condition is occurred.

Now, short talk over genetic operators.

3.2 Genetic Operators

Genetic operators are such operators like + - / * we used in math. They are used for generation and pruning operations in Genetic Algorithm. They have arguments we need to set in case of our problem.

3.2.1 Crossing-Over

This operator is used to combine existing solutions into others, by this way it maintains genetic diversity. In GAF, crossing-over operation could be done with two options; Single Point and Double Point crossing-over. They are illustrated below:

Single Point Crossing-over

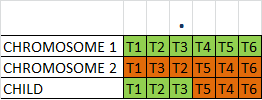
Single Point crossing-over operation takes two chromosomes, randomly selects an index, takes preceding section from chromosome-1 and succeeding section from chromosome-2 and generates a new one.

Double Point Crossing-over

In many cases, using Double Point crossing-over is more appropriate. It selects two points and swaps the center section between parents.

This is how we define a crossing-over operator in GAF:

(From blog of John Newcombe)

var crossover = new Crossover(crossoverProbability, true)
{
   CrossoverType = CrossoverType.SinglePoint
}; 

The crossover probability is simply a value between 0 and 1 that represents the probability of parents crossing over to produce children. A value of 1 means that all selected parents will crossover and create children. A value of 0.85 means that 85% will be crossed over and the remainder of parents will be pass through untouched to the new generation. The second parameter relates to duplicate handling.

3.2.2 Mutation

The mutation operators operate on one chromosome, It simply swaps the values of some randomly chosen genes of a chromosome. This operator maintains genetic diversity too.

Mutation

This is how we define a mutation operator in GAF:

var mutate = new SwapMutate(mutationProbability);  

3.2.3 Elite

Elitism allows the best solutions to pass through to the next generation without being modified. For example, a value of 5 percent with a population of 100, means that the top 5 chromosomes form part of the next generation. This means that any future generation is at least as good as the current generation. Elitism helps protect good individuals. However, it can be shown that as the percentage of elites is increased, the number of duplicates within the population increases, thereby reducing the performance of the GA.

This is how we define an elite operator in GAF:

var elite = new Elite(elitismPercentage);  

4. Perfect Matching Problem

Given a graph G = (V,E), a matching M in G is a set of pairwise non-adjacent edges; that is, no two edges share a common vertex. A perfect matching is a matching which matches all vertices of the graph. That is, every vertex of the graph is incident to exactly one edge of the matching. A perfect matching is also a minimum-size edge cover (from wiki). To able to solve this problem, vertex count must be even.

In the above figure, only part (b) shows a perfect matching. Now assume that, edge lengths are not equal and we are trying to find the best perfect match that results shortest edge length sum. At this point, the problem becomes more complex. If we have a tetragonal with A, B, C, D vertices, all possible solutions are:

1. A-B , C-D => 7 + 4 = 11
2. A-C, B-D => 5 + 3 = 8
3. A-D, B-C => 6 + 11 = 17

Second solution costs 8, it is the best match. It is easy with a tetragonal, what if it was hexagonal?

15 possible solutions. Defining all of them and calculating total weight seems harder now. If we have 8 vertices, solution count will be 105 and it goes as 945, 10395, 135135, 2027025... complexity grows faster.

Its complexity is n!! which is called Double Factorial.

For example, 9!! = 1 × 3 × 5 × 7 × 9 = 945.

5. Fixture Generation Problem

League fixture generation is used in various area, I will talk over a particular one, Swiss Patton technique to match teams in Bridge game. We need to generate n-1 rounds for n team, here are the requirements of this problem:

• Team count shall be even.
• Each pair shall be matched only one time.
• Consider to match close score teams.
• Create all possible rounds (if team count is n, n-1 possible rounds shall be created).

Yes, this problem is exactly same with "Perfect Matching Problem", think of each team as a vertex of a polygonal:

We will generate possible best matches each round, and using genetic algorithm seems very appropriate for this situation.

6. Using the Code

I constructed a Model to hold application data; it consists of Player, Team, Match, Round and Session classes.

Player class holds player id and player name.

[Serializable] 
public class Player
{
    #region Fields
    private string _id;
    private string _name;
    #endregion
    #region ctor
    public Player()
    {
        _id = Guid.NewGuid().ToString();
        _name = "Player";
    }
    public Player(string name)
    {
        _id = Guid.NewGuid().ToString();
        _name = name;
    }
    #endregion
    #region Properties
    [Browsable(false)]
    public string Id
    {
        get { return _id; }
        set { _id = value; }
    }
    public string Name
    {
        get { return _name; }
        set { _name = value; }
    }
    #endregion
}  

Team class holds team id, team name, total score, last rank, previous matched teams and player list.

[Serializable]
public class Team
{
    #region Fields
    private string _name;
    private string _id;
    private int _score;
    private int rank;
    private List<Team> _matchedTeams;
    private Team _currentMatch;
    private List<Player> _players;
  
    #endregion
    #region ctor
    public Team()
    {
        _matchedTeams = new List<Team>();
        _name = "Team";
        _score = 0;
        rank = 0;
        _id = Guid.NewGuid().ToString();
    }
    public Team(string name = "Team", int score = 0)
    {
        _matchedTeams = new List<Team>();
        _name = name;
        _score = score;
        _id = Guid.NewGuid().ToString();
    }
    #endregion
    #region Properties
    [Browsable(false)]
    public string Id
    {
        get { return _id; }
        set { _id = value; }
    }
    public string Name
    {
        get { return _name; }
        set { _name = value; }
    }
    public int Score
    {
        get { return _score; }
        set { _score = value; }
    }
    public List<Player> Players
    {
        get { return _players; }
        set { _players = value; }
    }
    [Browsable(false)]
    public Team CurrentMatch
    {
        get { return _currentMatch; }
        set { _currentMatch = value; }
    }
    [Browsable(false)]
    public List<Team> MatchedList
    {
        get { return _matchedTeams; }
        set { _matchedTeams = value; }
    }
    public int Rank
    {
        get { return rank; }
        set { rank = value; }
    }
    #endregion
    #region Methods
    public override string ToString()
    {
        return _name + " - (" + _score + ")";
    }
    public bool IsMatchedBefore(Team team)
    {
        return _matchedTeams.Contains(team);
    }
    #endregion
} 

Match class holds a team pair that are matched.

[Serializable]
public class Match
{
    #region Fields
    /// <summary>
    /// Home team field of class
    /// </summary>
    private Team _homeTeam;
    /// <summary>
    /// Away team field of class
    /// </summary>
    private Team _awayTeam;
    #endregion
    #region ctor
    /// <summary>
    /// Initializes a new instance of the Match class, that matches two teams for a round
    /// </summary>
    /// <param name="home">Pass team for this parameter which holds for "Home Team"</param>
    /// <param name="away">Pass team for this parameter which holds for "Away Team"</param>
    public Match(Team home, Team away)
    {
        this._homeTeam = home;
        this._awayTeam = away;
    }
    #endregion
    #region Properties
    /// <summary>
    /// Gets or sets "Home Team" for current match object
    /// </summary>
    public Team HomeTeam
    {
        get { return this._homeTeam; }
        set { this._homeTeam = value; }
    }
    /// <summary>
    /// Gets or sets "Home Team" for current match object
    /// </summary>
    public Team AwayTeam
    {
        get { return this._awayTeam; }
        set { this._awayTeam = value; }
    }
    #endregion
    #region Methods
    /// <summary>
    /// Overrides ToString() method of class to visualize a better string representation
    /// </summary>
    /// <returns>Name of "Home Team" vs "Away Team"</returns>
    public override string ToString()
    {
        if (_homeTeam == null || _awayTeam == null)
            return "Empty Match!";
        return _homeTeam.Name + " (" + _homeTeam.Score + ") vs " + 
        _awayTeam.Name + " (" + _awayTeam.Score + ")";
    }
    #endregion
} 

Round class holds round ID and matches list, list count will be half of team for each round.

[Serializable]
public class Round
{
    #region Fields
    private List<Match> _matches;
    private int _id;
    #endregion
    #region ctor
    public Round()
    {
        _matches = new List<Match>();
    }
    public Round(List<Match> matches)
    {
        _matches = matches;
    }
    #endregion
    #region Properties
    public List<Match> Matches
    {
        get { return _matches; }
        set { _matches = value; }
    }
    public int Id
    {
        get { return _id; }
        set { _id = value; }
    }
    #endregion
    #region Methods
    public List<Match> AddMatch(Match match)
    {
        _matches.Add(match);
        return _matches;
    }
    public override string ToString()
    {
        if (_matches.Any())
        {
            return "Round: " + _id + Environment.NewLine + string.Join("\r\n", _matches) + "\r\n";
        }
        return "Round: No matches!";
    }
    #endregion
} 

Session class holds rounds list.

[Serializable]
public class Session
{
    #region Fields
    private List<Round> _rounds;
    #endregion
    #region ctor
    public Session()
    {
        _rounds = new List<Round>();
    }
    #endregion
    #region Properties
    public List<Round> Rounds
    {
        get { return _rounds; }
        set { _rounds = value; }
    }
    #endregion
    #region Methods
    public List<Round> AddRound(Round round)
    {
        _rounds.Add(round);
        return _rounds;
    }
    public Round CreateARound(List<Match> matches)
    {
        if (matches != null && matches.Any())
        {
            var round = new Round(matches) {Id = Rounds.Count + 1};
            _rounds.Add(round);
            return round;
        }
        return null;
    }
    public override string ToString()
    {
        return "Round Count: " + _rounds.Count;
    }
    #endregion
} 

And Model holds team list and session.

[Serializable]
public class Model
{
    #region Fields
    private List<Team> _teams;
    private Session _mySession;
    #endregion
    #region ctor
    public Model()
    {
        _teams = new List<Team>();
        _mySession = new Session();
    }
    #endregion
    #region Properties
    public List<Team> Teams
    {
        get { return _teams; }
        set { _teams = value; }
    }
    [Browsable(false)]
    public Session MySession
    {
        get { return _mySession; }
        set { _mySession = value; }
    }
    #endregion
    #region Methods
    public void AddRandomPointsToTeams()
    {
        _teams.ForEach(p => p.Score += Util.Util.RandomNumber(31));
    }
    public List<Team> AddTeam(Team team)
    {
        _teams.Add(team);
        return _teams;
    }
    public List<Round> AddRound(Round round)
    {
        _mySession.AddRound(round);
        return _mySession.Rounds;
    }
    public Round CreateARound(List<Match> matches)
    {
        return _mySession.CreateARound(matches);
    }
    public void ClearHistory()
    {
        _mySession.Rounds.Clear();
        _teams.ForEach(p =>
        {
            p.Score = 0;
            p.Rank = 0;
            p.MatchedList.Clear();
            p.CurrentMatch = null;
        });
    }
    public bool IsGameEnd()
    {
        return (_mySession.Rounds.Count == _teams.Count - 1);
    }
    #endregion
} 

And now we are ready for calculations:

• I will create a population (I decided to create 100, but it can be several hundreds or thousands in case of problem),
• Set its chromosome length (equals team count for our problem).
• Define and add genetic operators.
• Define "Fitness Calculation" method that takes chromosome as input and returns double.
• Pass population and fitness calculation method to genetic algorithm object.
• Define a "Termination" method and run genetic algorithm by passing this method as delegate to it.

Generation count is a preset value, 1000 generation is working good for 20 teams. There's no optimal generation count, GAs are about 'near enough is good enough'. You simply have to decide what is good enough.

public List<Match> PickaMatchList()
{
    var lastListMatch = new List<Match>();
    double diffTotal = 0.0;
    var population = new Population(_teams.Count);
    for (var p = 0; p < 100; p++)
    {
        var chromosome = new Chromosome();
        for (var g = 0; g < _teams.Count; g++)
        {
            chromosome.Genes.Add(new Gene(g));
        }
        //mix each chromosome up and add to the population
        chromosome.Genes.Shuffle();
        population.Solutions.Add(chromosome);
    }
    //create the elite operator
    var elite = new Elite(5);
    var crossover = new Crossover(1.0)
    {
        CrossoverType = CrossoverType.DoublePointOrdered
    };
    //create the SwapMutate operator
    var mutate = new SwapMutate(0.2);
    var ga = new GeneticAlgorithm(population, CalculateFitness);
    //subscribe to the generation and run complete events
    ga.OnGenerationComplete += (sender, e) =>
    {
        if (OnGenerationComplete != null)
            OnGenerationComplete(sender, e);
    };
    ga.OnRunComplete += (sender, e) =>
    {
        var fittest = e.Population.GetTop(1)[0];
        for (int i = 0; i < fittest.Genes.Count; i += 2)
        {
            lastListMatch.Add(new Match(_teams[(int)fittest.Genes[i].RealValue],
                _teams[(int)fittest.Genes[i + 1].RealValue]));
        }
        diffTotal = CalculateDifference(fittest);
    };
    //add the operators
    ga.Operators.Add(elite);
    ga.Operators.Add(crossover);
    ga.Operators.Add(mutate);
    //run the GA
    ga.Run(Terminate);
    if (diffTotal >= _falseStateConstant)
        return null;
    lastListMatch.ForEach(p =>
    {
        p.HomeTeam.CurrentMatch = p.AwayTeam;
        p.AwayTeam.CurrentMatch = p.HomeTeam;
        p.AwayTeam.MatchedList.Add(p.HomeTeam);
        p.HomeTeam.MatchedList.Add(p.AwayTeam);
    });
    return lastListMatch;
} 

The return value of fitness function needs to be between 0 and 1 with the better fitness being the higher number.

private double CalculateFitness(Chromosome chromosome)
{
    var diffTotal = CalculateDifference(chromosome);
    _generationCount = diffTotal == 0 ? 1 : _tempGenerationCount;
    return 1 - diffTotal / (_falseStateConstant * _teams.Count);
} 

The significant point is how the fitness calculation is implemented.

Chromosome gives us a series of array index, we need to map these values to real data. Then group elements by pairs and calculate rank difference between them. If them pairs are matched before, add a big number as difference, it will result a bad fitness value and leads algorithm discards this chromosome immediately.

private double CalculateDifference(Chromosome chromosome)
{
    var diffTotal = 0.0;
    for (int i = 0; i < chromosome.Genes.Count; i += 2)
    {
        var teamHome = _teams[(int)chromosome.Genes[i].RealValue];
        var teamAway = _teams[(int)chromosome.Genes[i + 1].RealValue];
        if (!teamHome.IsMatchedBefore(teamAway))
        {
            var difference = Math.Abs(teamHome.Rank - teamAway.Rank);
            diffTotal += difference;
        }
        else
        {
            diffTotal += _falseStateConstant;
        }
    }
    return diffTotal;
} 

private bool Terminate(Population population, int currentGeneration,long currentEvaluation)
{
    return currentGeneration > _generationCount;
} 

And at the end of each round, new scores are added to teams and before generating next round, ranks are recalculated via this extension method;

public static void SortTeams(this List<Team> list)
{
    list.Sort((a, b) => (b.Score.CompareTo(a.Score)));
    for (int i = 0; i < list.Count; i++)
    {
        list[i].Rank = i;
    }
}   

7. Conclusion

Genetic Algorithms (GAs) are the nearest thing a software developer can get to magic. I generated 35^th round with 40 teams, less than 5 minutes. It can take up months with classical methods. And GAF opened a few doors for me, it is really good implemented and extensible, you can even create your own Genetic operator easily. Was a good experience for me, thanks for reading.

8. History

• 25.05.2014 - Initial version