Second Order Görtzel Algorithm
There are many descriptions about the second order Goertzel algorithm to be found in the net. But most of them do not explain its derivation in full. There is always the same part missing. So I try to fill this gap. :)
The second order Goertzel algorithm is based on the transfer function of the first order Goertzel algorithm:
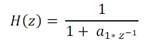
with:

Multiplying the enumerator and denominator by 1 + conjugate of a1 * z^-1 makes the denominator a real value and leads to:

And from this to the difference equation:
c[n] + a1 * c[n-1] + c[n-2] = y[n] + b1 * y[n-1]
with:
a1 = -2 cos(2kp/N) and b1 = -exp(-j2kp/N)
For a long time, I was wondering why they are doing this. The difference equation looks much more complicated now. But there is some advantage at the end. :)
Here, all the explanations now say: “As we are only interested in c[n], we can leave the complex multiplication b1 * y[n-1] till the end of the calculation and have to carry it out only once at the end”… That’s not the whole truth. We are interested in c[n] and the complex calculation can be put to the end of the calculations. But there is no relation between these two things. It took me a deep look into the theories of digital signal processing to find out why. :)
The big step lays in the signal path. The signal path to the difference equation further above looks like:

If we would implement this, it would be something like...
c[n] = y[n] + b1 * y[n-1] - a1 * c[n-1] - c[n-2]
...put into a loop and in each cycle, the complex multiplication b1 * x[n-1] and due to that, the whole calculation has to be carried out complex. Much more calculation effort than required in the first order Goertzel algorithm. That’s not what we want.
The signal path can be drawn like this:

Now, we have two independent transfer functions and these two functions can be switched without influencing the resulting transfer function.

And be put together again. This form is called the direct form II of the signal path and looks much better. The feedback part is now at the beginning of the function.

This put into code, we get:
v[n] = y[n] –a1 * v[n-1] – v[n-2]
for the left feedback part,
and:
c[n] = v[n] + b1 * v[n-1]
for the right feed forward part.
That’s the big benefit. The rather complicated difference equation leads to a very short and quick algorithm just by changing the drawing of the signal path. A very impressive interaction of Mathematics and pure theories of digital signal processing (and the guy who did this, Gerald Goertzel, is really admirable?)
The feedback part has to be implemented in a loop running through all the samples of y. That means from 0 to N-1.
for (n = 0; n < N; n++)
{
v0.real = y[n].real - a1.real * v1.real - v2.real;
v2 = v1;
v1 = v0;
}
I used complex data types because at the end we have complex numbers.
The right part needs to be calculated only once at the end of the calculation (and it has nothing to do with the fact that we are looking for c[n] only ?). Basically the right part contains the complex multiplication v[n-1] * b1. So far, we only had real values to deal with. That means v[n-1] is real and has no imaginary part. Therefore, the following complex multiplication becomes not very complicated. The real part becomes v[n-1]. real * b1.real and the imaginary part becomes v[n-1].real * b1.imag. Finally, we are looking for the Fourier components a[n] = c[n].real*2 and b[n] = -c[n].imag*2. Both values should be calculated as c[n] = v[n] + b1 * v[n-1]. Now for the real part, that’s:
c[k].real = (v0.real + b1.real * v2.real);
As v[n] is a real value and has no imaginary part. The calculation for the imaginary part c[k].imag becomes a bit shorter:
c[k].imag = -(b1.imag * v1.real);
And finally both values have to be divided by N because of:

With this, the sequence for all the Fourier components a[0] to a[N-1] and b[0] to b[N-1] is:
for (k = 0; k < N; k++)
{
v0.real = 0;
v0.imag = 0;
v1.real = y[1].real;
v1.imag = y[1].imag;
v2.real = y[0].real;
v2.imag = y[0].imag;
b1.real = -Math.Cos((double)(2.0 * Math.PI * (double)(k) / (double)(N)));
b1.imag = Math.Sin((double)(2.0 * Math.PI * (double)(k) / (double)(N)));
a1.real = -2 * Math.Cos((double)(2.0 * Math.PI * (double)(k) / (double)(N)));
a1.imag = 0;
for (n = 0; n < N; n++)
{
v0.real = y[n].real - a1.real * v1.real - v2.real;
v2 = v1;
v1 = v0;
}
c[k].real = (v0.real + b1.real * v2.real) / (double)(N) * 2.0;
c[k].imag = -(b1.imag * v1.real) / (double)(N) * 2.0;
}
And at the end it takes
c[0].real = c[0].real / 2;
c[0].imag = c[0].imag / 2;
Implemented like this, the second order Goertzel algorithm is a very fast way to carry out a Discrete Fourier transformation. On my computer, the test application with 1000 samples takes 8 ms. A standard implementation of the Discrete Fourier transformation takes 120 ms for the same calculation. But this increase of calculation speed costs some accuracy and the Goertzel algorithm is not stable if the number of samples gets too big. Already in my test application, some inaccuracy is visible. For the rectangle signal, all the real parts should become 0. But a[1] = -0.12, a[2] = 0.04, a[3] = -0.11 and so on. In the standard implementation, a[1] = 0.04, a[2] = 0.04, a[3] = 0.04 for the phase shift of the harmonics that can make quite a difference.
Regarding stability, I read the Reinsch algorithm is an improved version of the second order Görtzel algorithm and it would be stable. So, I implemented this one too for comparison.
Reinsch Algorithm
The Reinsch algorithm is a modified Görtzel algorithm.
For cos(2Pi*k/N) > 0 Reinsch takes the part
v[n] = y[n] - a1 * v[n-1] - v[n-2]
and says for the difference between v[n] – v[n-1]
v[n] - v[n-1] = y[n] - a1 * v[n-1] - v[n-2] - v[n-1]
he expands this equation by +2 * v[n-1] and – 2 * v[n-1] and as a1 = -2cos(2Pi*k/N), he gets
v[n] - v[n-1] = y[n] + (2cos(2Pi*k/N) - 2) * v[n-1] + v[n-1] - v[n-2]
Now there are two substitutions:
(2cos(2Pi*k/N) - 2) = - 4 * sin(Pi*k/N)^2
And with v[n] – v[n-1] = dv[n], the last two terms v[n-1] – v[n-2] = dv[n-1],
we get:
dv[n] = y[n] - 4 * sin(Pi*k/N)^2* v[n-1] + dv[n-1]
and finally for v[n]:
v[n] = dv[n] + v[n-1]
This is a loop with dv[n] as feedback part and looks like:
a1.real = - 4 * Math.Pow(Math.Sin((double)(Math.PI * (double)(k) / (double)(N))), 2.0);
a1.imag = 0;
we[k] = a1.real;
for (n = 0; n < N; n++)
{
dW = y[n].real + a1.real * v1.real + dW;
v0.real = dW + v1.real;
v1 = v0;
}
c[k].real = (dW - a1.real / 2.0 * v0.real) / (double)(N) * 2.0;
c[k].imag = (b1.imag * v1.real) / (double)(N) * 2.0;
For cos(2Pi*k/N) >= 0 Reinsch takes the sum instead of the difference:
v[n] + v[n-1] = y[n] - a1 * v[n-1] - v[n-2] + v[n-1]
and gets
(2cos(2Pi*k/N) + 2) = 4 * cos(Pi*k/N)^2
and
v[n] = dv[n] - v[n-1]
and that’s like:
a1.real = 4 * Math.Pow(Math.Cos((double)(Math.PI * (double)(k) / (double)(N))), 2.0);
a1.imag = 0;
we[k] = a1.real;
for (n = 0; n < N; n++)
{
dW = y[n].real + a1.real * v1.real - dW;
v0.real = dW - v1.real;
v1 = v0;
}
c[k].real = (dW - a1.real / 2.0 * v0.real) / (double)(N) * 2.0;
c[k].imag = (b1.imag * v1.real) / (double)(N) * 2.0;
So I could compare these two algorithms and that was a bit disappointing.
The instability of the Görtzel algorithm was caused by extinction of numbers after floating point in earlier time. That could have happened if the whole algorithm was implemented with float variables which had a precision of 7 digits after floating point. Implemented like this with more than 28000 samples cos(2Pi*k/N) got 1.0 with k = 1. But nowadays with double values, this does not happen anymore. So the two algorithms behave the same still with 100000 samples. That means there is no need for a Reinsch algorithm as long as the DFT is performed on a modern 64 Bit computer and is implemented in a modern language like C# :-)
The second order Goertzel algorithm is a very quick thing but it has its disadvantages. Regarding accuracy, the same is valid for the Reinsch algorithm I made a bit a quicker implementation of the Discrete Fourier transformation by putting the calculations of all the used exp(j2k /N) values into an array and picking them from there. With this algorithm, the same transformation runs in 20 ms and is as accurate as the standard implementation. See:
That could be a good alternative. :-)
But nevertheless, the second order Görtzel as well as the Reinsch algorithm, both are very sophisticated algorithms and both are a big effort in mathematics and informatics.
