Introduction
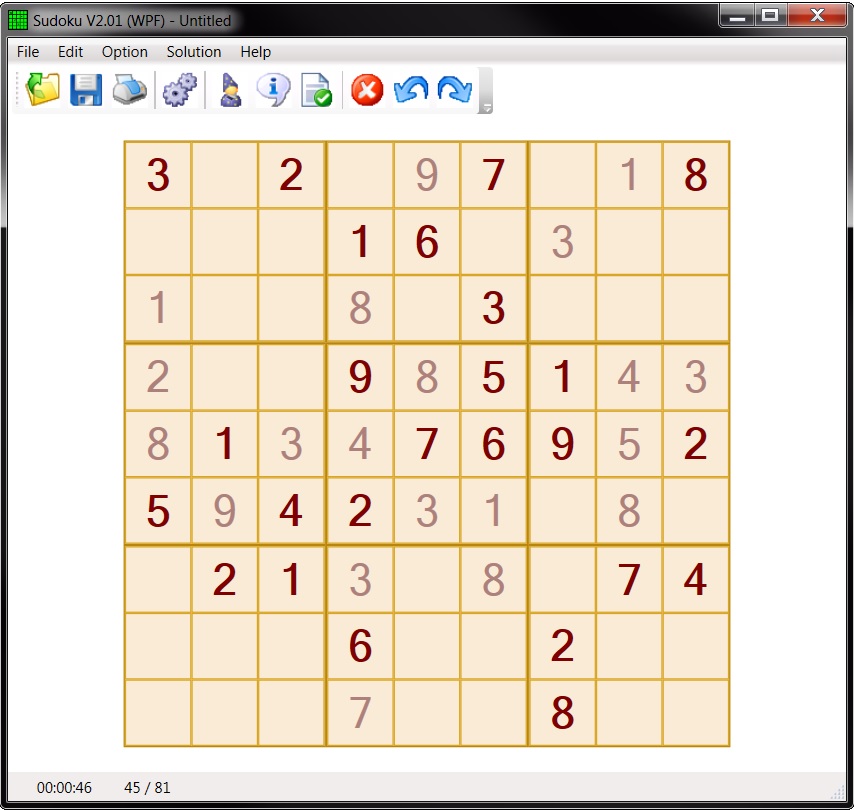
Sudoku is a program built in C# with a WPF user interface. It can generate 9x9 or 16x16 boards at easy, medium or advanced level. I programmed it years ago and finally decided to publish it seeing that it implements some functions not found in the other postings.
Features
This sudoku program features:
- 9x9 or 16x16 boards with different difficulty levels
- Resolution of any 9x9 or 16x16 Sudoku puzzle
- Customizable fonts and colors
- Customizable symbols used to represent values (numbers, letters or symbols)
- Choices of input modes: cell toggle or value picker
- Input value modes which accepts only valid values or accepts any values
- Printing of sudoku boards (the current one or in batch)
- Designing your own sudoku (design mode)
- Saving or loading of a sudoku board
- Undo / redo functions
- Different kinds of hints
- Etc.
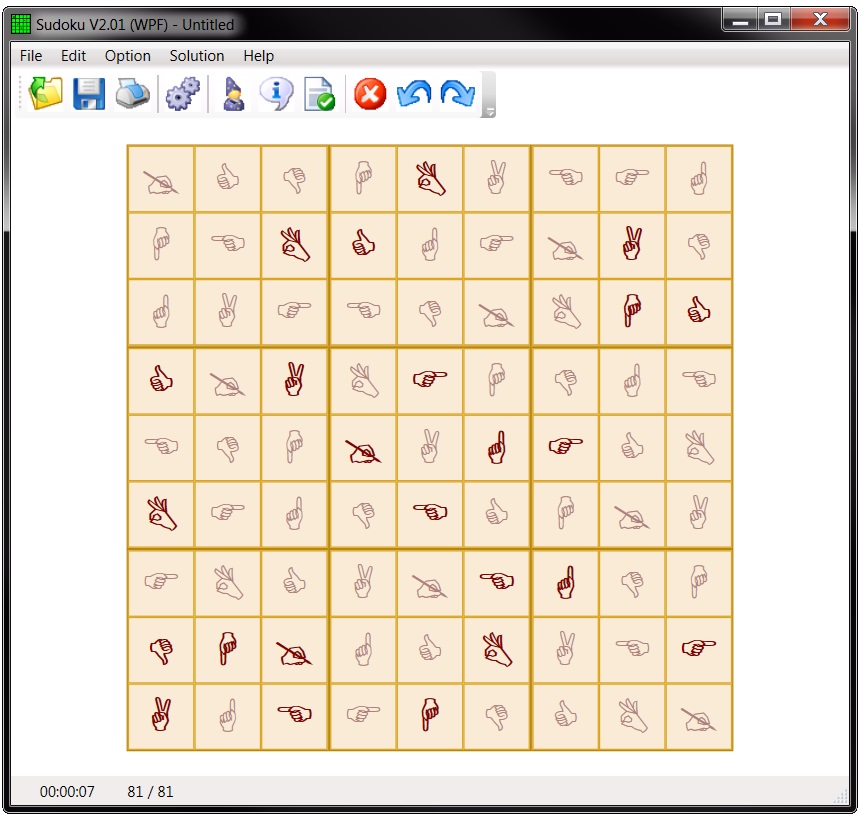
Sudoku board using symbols instead of numbers
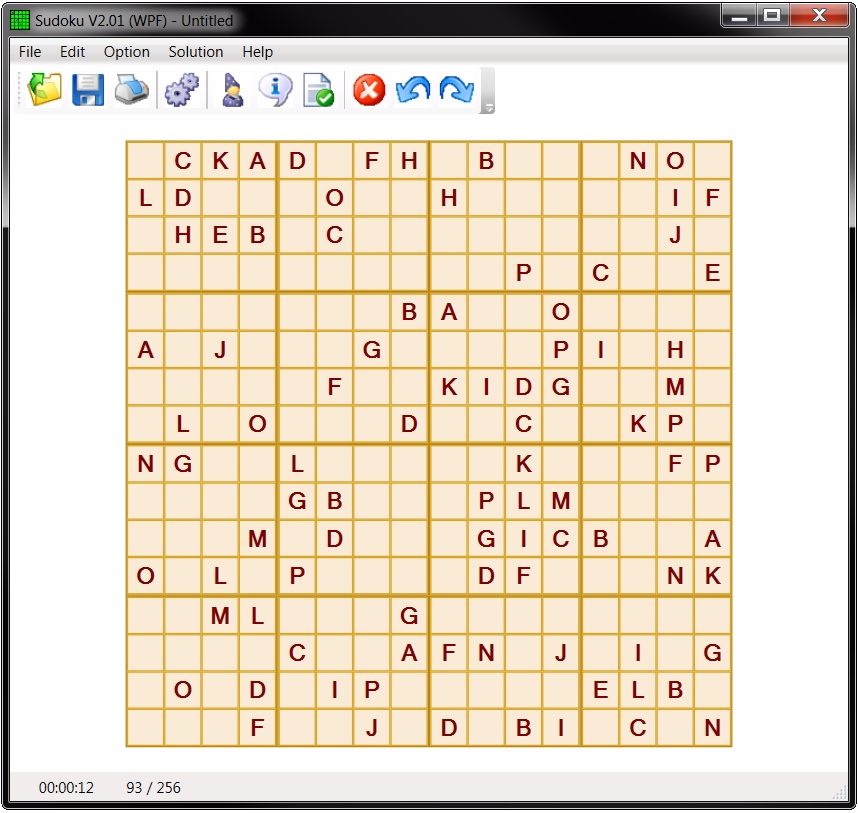
16x16 Sudoku board using letters instead of numbers
Versioning
| Version 2.01 | Original posted version.
| |
Demo Provided
The provided demo is the sudoku program in C# with the WPF interface.
Sources Provided
In addition to the source of the provided demo, I also include a prior version of this program written using Windows Forms. This latter version is not supported.
What Needs to be Improved?
- It would be nice to be able to annotate the board.
- I saw interesting input methods in other Sudoku games which can be added to this version.
- The level difficulty can be more subtle.
- Adding a help file to the game would be welcome.
Source Description
The main classes included in the project are:
Engine Classes
- CellPos: Cell position (x,y)
- SudBoard: Abstract class implementing the sudoku board
- SudBoard9: SudBoard implementation for a 9x9 board
- SudBoard16: SudBoard implementation for 16x16 specific functions
- SudBoardGenerator: Generates 9x9 or 16x16 board synchronously or asynchronously
- ValCount: Abstract class implementing a counter for each possible value for a type of region (lines, squares or columns)
- ValCount9: ValCount implementation for a 9x9 board
- ValCount16: ValCount implementation for a 16x16 board
WPF and User Interface Classes
- app: Application
- dlgAbout: About box
- dlgBoardAppearance: Dialog box to change the fonts and colors used to draw the interface
- dlgGenerateABoard: Dialog box to handle board generation
- SudControl: Visual control inheriting from UserControl and holding a sudoku board (SudBoard)
- ValPickerControl: Implements the value picker used to choose what value to play. Used by SudControl
- wndMain: Main window
1. Data Structures
The values are stored in the single dimension array int[] m_arrBoardVal. The use of a single dimension array instead of a two dimension array improves significantly the performance. The values in the array range from 0 to 9 (for 9x9 board) or 0 to 16 (for 16x16 board). Value 0 denotes an empty cell. The first value of the array is used to store the upper left cell value while the last one is used to store the bottom right value.
The range of values stored in the single dimension array ValueTypeE[] m_arrBoardValType:
| None (0) | Empty cell |
| Fix (1) | Fixed value. User cannot change it |
| User (2) | Value user can change |
The ValueCount class is designed to keep the count of values for lines, columns and squares. Each time a cell value is updated, the ValCount of the line, the column and the square where the cell is located are updated accordingly.
| m_LineValCount | Keeps the count of each possible value for each line |
| m_ColValCount | Keeps the count of each possible value for each column |
| m_SqrValCount | Keeps the count of each possible value for each square |
The program needs to convert a linear position to a line/column and square position. These conversions are heavily used and must be optimised (especially with 16x16 board). The conversion in a 16x16 board is done with multiplication and modulo by 16. These operations are done using bit shifts and the '&' operator. This is the reason why the classes SudBoard9/16 and ValCount9/16 exist.
The conversion from square position to linear position is done using these two arrays:
| m_arrPosToSqr | Linear position -> Square position |
| m_arrSqrToPos | Square position -> First linear position of the square |
The sudoku board class supports the undo or redo moves. To do so, two stacks hold the moves which can be undone or redone:
| Stack<Move> m_stackUndoMoves |
| Stack<Move> m_stackRedoMoves |
2. Moves
A move is defined has being valid if the value being entered is unique in its column, its line and its square.
The main method to change the value of a cell is PlayAt. The method updates the m_arrBoardVal and m_arrBoardValType arrays. It updates the corresponding square, line and column ValCount instances. If specified, the undo and redo stacks are updated.
3. Solving a board
A given sudoku board can have no solution, one solution or more than one solution. A solving method must be able to find a board solution if it exists and to indicate if more than one solution is possible.
A simple backtracking method can be enough to solve a 9x9 board.
while No Solution Found
Find the first empty cell
For each possible value in this cell
Play it
Call recursively
If Solved
Solution Found, exit
Else
Undo the move
EndIf
Next
Oops, bad board!
wend
However, using this simple approach for solving a 16x16 board is too slow (at least to generate a 16x16 board where the Solve method has to be called many times). A better approach is to use an improved backtracking method:
do {
Fill the obvious cells
If solution not found,
Find the first empty cell
For each possible value in this cell
Play it
Call recursively
If solve
Solution Found, exit
Else
Undo the move
EndIf
Next
Oops, bad board!
EndIf
} while No solution found
A way to improve further the performance is to compute the list of possible moves in advance. The problem is now to implement the "Fill the obvious cells". In this context, obvious means:
- A value which can be played in only one cell of a square, a line or a column.
- A cell in which only one value can be played.
| FillListOfValidValuesForEmptyCells | Fills an array with the list of possible moves |
| FillValueWhichCanBePlayedInSingleCellOfAZone | Fills all cells where a value can be played in only one line, one column or one square. |
| FillObviousCells | Fills all obvious values |
| SolveBacktrack | Improved backtracking method |
| Solve | Solves the board |
4. Generating a sudoku board
The different objectives of this board generator are:
- To generate a valid board which has one and only one solution.
- To generate a 9x9 or 16x16 board.
- To generate different levels of boards (easy, medium and difficult).
The computer uses three strategies to solve a board:
- Fill cells with a value which can be played in only one cell of a square, a line or a column.
- Fill cells where only one value can be played.
- Brute force (try permutations one by one)
For humans, the first method is the easiest, the second one is more difficult and the third is the most difficult. An easy board needs only the first method to be solved. A medium board needs the first two methods while a difficult board needs the three methods to be solved.
The general approach used by this program to generate a board is:
- To generate a completed board
- To remove values one by one as long as:
- There is only one solution to the board
- Only strategies compatible with the difficulty level are being used
The board generation is done by the SudBoardGenerator class. The board can be generated on the main thread or on a worker thread.
4.1 Generating a completed board
A board can be filled using a simple backtracking method:
Fill(iPos)
If Board Filled,
Return
ForEach Value
If Value is valid at this position
Play it
If Fill(iPos+1) = Filled
Return
Else
Undo the move
EndIf
EndIf
Next
<Must never get here>
This method will always give the same board. To make a random board generation, we just shuffle the order of the filled position.
In general, generating a completed board using this method is quite fast. However, from time to time, some 16x16 boards can take a long time to complete. When it happens, it's faster to cancel this generation and restart it.
4.2 Shaving the board (Digging holes)
Once a completed board has been generated, we just have to remove values from random cells:
ForEach Pos in Random Order
Set the position value to 0
If Solve doesn't give 1 solution or used strategies not compatible with the expected difficulty level
Restore the value
EndIf
Next
On a 16x16 board, this routine can take a relatively long time. For this reason, a timeout can be provided. If the timeout is reached, the board will still be valid but will contain more completed cells.
5 Sudoku Control
The SudControl implements a visual control inheriting from System.Windows.Controls.UserControl. It's used to play sudoku.
