Introduction
Lately, I've been playing around some more with Linq Expression trees. They're pretty awesome, but for some reason the examples don't seem to move beyond creating a simple hardcoded expression and executing it. Nice from an academic point of view, but since the expression was hardcoded, it's never going to change its behaviour and might as well have been written in plain C#. So I tried a little project do create them on the fly.
To be able to create expressions dynamically, we need some way to change the definition they're created from. This could be an XML document, but I thought it would be nice to write a very simple parser, because that's where ExpressionTrees usually come from. (Yes kids, really! They don't come from the stork, time to man up now and face parsers ;-).)
In this article, I'll present a very simple expression language that I'll call TinyLisp. The program with this article evaluates expressions written in it and displays the result. It uses Linq.Expressions under the hood to make all that work. You can enter an expression and see how it's parsed into an abstract syntax tree, then converted to a Linq expression tree and finally executed.
Here's what we're going to cover:
- First, we will design our little language. We'll cut some smart corners here, so the rest can be done within one article.
- Then, we'll write the code to parse these expressions. This will be a lot easier than you might expect. Because of how we designed our language, we can actually write this parser in one method.
- Now that we have our parser that creates abstract syntax trees, we need something that will transform them into
Linq.Expression trees. There's a little difference between our language and Linq that we need to bridge, so we'll need to rewrite that tree. - Now we're home free! Compiling and executing Linq Expressions is something kids and grannies do nowadays, so we'll only briefly touch on that.
So without further ado, let's design that little language.
The Language
The main design goal of our language is that it should be extremely easy to parse. We'll do that by writing down expressions in a bit of an unusual way. Here's an expression written in our language, that we will call TinyLisp.
(+ 1 2 3)
It looks a little strange at first because it is written in prefix notation that probably needs a little explanation. In school, we were taught to write that same expression like this:
1 + 2 + 3
This is called infix notation. The plusses are the operators, and 1, 2 and 3 are the operands that they operate on. With infix notation, the operator sits between two operands. In our prefix notation, the operator is in front of the operands, and they're all surrounded by parentheses.
Note that with prefix, we only needed 1 operator for 3 operands. Because they are within parentheses, there can be as many operands as you like. To do that in infix, you need to chain the operators between each pair of operands. That's why we needed 2 plusses for infix. This is the little difference between the two I mentioned that we'll have to bridge later on.
Now see another expression written in infix:
5 + 4 * 3 + 2 / 1
This is a bit of a pickle with infix notation. To work out that the answer is 19, you need to know that division comes before multiplication, and that multiplication comes before addition. There's plenty of theory on how to parse infix notation, but it would complicate our parser way too much. This article is more about Linq Expressions, so we want to simplify our job. We'll apply the precedence rules ourselves and add parentheses to indicate the order of evaluation:
5 + (4 * 3) + (2 / 1)
That's better already, but when we'd try to parse this it would still be little complicated because of the order in which the expressions appear. When we move the operator to the front of each (sub)expression, we get this, which is the prefix notation syntax we're after:
(+ 5 (* 4 3) (/ 2 1))
Now the user has put in the parentheses himself which saves the parser a lot of thinking. Apart from that, the order is very convenient. We first get our operator, then the operands, and the entire expression is neatly enclosed within parentheses. This sequential flow from left to right allows our parser to be very simple.
Our language definition in EBNF now looks like this:
expression = '(' ( '+' | '-' | '*' | '/' ) [ ['0'..'9'] | expression ]+ ')'
In normal words: an expression consists of an opening parenthesis, then one of these operands +,-,*,/ then one or more integers or expressions, and finally a closing parenthesis.
As an extra corner we can cut, we will only deal with the numbers [0 .. 9], and only with operators: [+, -, *, /]. This way, every thing we will encounter is just 1 character long. Or, every single character is a token. In short, a token is like a word in a sentence. I won't elaborate on these topics here, if you're interested, check here. The point here is that we only need to enumerate the chars in the string to get a stream of tokens. We can do that.
Parsing Our Language
Parsing means to take a string and convert that into something a computer can understand: an abstract syntax tree. To revisit our example, this expression...
"(+ 5 (* 4 3) (/ 2 1))"
... is just a bunch of chars to a computer. It needs to be turned into a tree structure that a program can work on:
+
/ | \
5 * '/'
/ \ / \
4 3 2 1
That's what our parser will do. But how you ask, aren't parsers difficult? Well, that's where that prefix notation really comes in handy. The language design we chose basically IS a tree notation. Each opening parenthesis '(' marks the beginning of an expression. The first character after that is the operator. Then come one or more operands that can either be an integer or a new subexpression. Finally the expression is closed with a closing parenthesis. Then this (sub)expression is done and we can return it. Let's write that down in a bit of pseudo code:
Expression GetExpression:
Check opening parenthesis
Get Operator
Loop:
Get next token
If token = '(' then Operands.Add GetExpression
If token = ')' break loop
If token in [0..9] then Operands.Add token
This is basically all we need to do to read these prefix expressions into a tree. Sounds doable. Below is the whole thing written down in C#, after this short introduction.
The method in the listing is actually the constructor of the class ExpressionNode. To use it, call something along these lines:
ExpressionNode n = new ExpressionNode("(+ 5 4)")
Instead of a normal string, the real thing takes an argument of type CharStream. This CharStream is a simple wrapper class I wrote that takes a string and then exposes the individual chars one by one. The reason this class is used over a normal string is that we use recursion to parse the string into a tree. When we return from a subcall, we want to continue on the string where the subcall left off, not where it started. By passing this CharStream by reference, we get exactly that behaviour. It also handles some simple chores like skipping whitespace.
So here's our parser:
public ExpressionNode(CharStream Stream) {
this.Start = Stream.Position;
this.StringExpression = Stream.Stream;
if (Stream.Current != '(') throw new Exception("a (sub)expression
must always start with a '(' at position " + Stream.Current);
Stream.MoveNext();
if (Operators.Contains(Stream.Current)) this.Operator = Stream.Current;
else throw new Exception("Unexpected character '" +
Stream.Current + "' at position " + Stream.Position +
".\n\nThe first character after the '(' at position " +
this.Start + " that started this (sub)expression
must be its operator [+, -, *, /].");
while (true) {
Stream.MoveNext();
if (Stream.Current == '(') {
this.Operands.Add(new ExpressionNode(Stream));
continue;
}
if (Stream.Current == ')') {
this.End = Stream.Position;
break;
}
if (Ints.Contains(Stream.Current)) {
this.Operands.Add(new IntNode(Stream.Current));
continue;
}
throw new Exception("Error, expecting either '(', ')' or [0 .. 9]");
}
}
That's it. It checks that the first character is a '(', then it reads the operator. Then it loops until the closing parenthesis looking for either integers or subexpressions. When it comes across a ')', it's done and returns the (sub)expression as a tree structure. I encourage you to step through this code in the debugger to see how it all fits together.
Rewriting our Tree
Here's our tree again. If you look at it closely, you can see that we have a little problem because the top '+' operator has three arguments: 5, * and /. That's a no-no in Linq Expressions, because that only has BinaryExpressions that take 2 operands.
+
/ | \
5 * '/' <<< 3 operands for the + operator on this line...
/ \ / \
4 3 2 1
The problem here is that we have 3 operands and each operator can only accept 2. What we can do is use 2 operators, where one is the child of the other. The top one has 1 operator left and the bottom 2, totalling the 3 operators we needed. Let's put that to practise on our tree:
The top + operator with 3 operands, splits off a new + operator. This new one takes the last two operands and becomes the righthand operand of the original. Now each operator has two operands and we're good.
+
/ \
5 + <<< this is the new node that was split off
/ \
* '/'
/ \ / \
4 3 2 1
Before we go to the code for that, however, there's another issue we need to tackle.
Converting our Syntax Tree to a Linq Expression Tree
Besides the need to have a definition for our expressions that we could change easily, there's another reason why we needed our own syntax tree. The reason is that you can't just put together a Linq expression tree together any way you like. Because of the way the constructors are defined, you're forced to create them bottom up. Take, for instance, the BinaryOperator that we need to evaluate our expressions, we can't just go and say:
BinaryOperator b = new BinaryOperator()
because you'll get this message:
Error 56 The type 'System.Linq.Expressions.BinaryExpression'
has no constructors defined
No constructors at all .. but .. then .. where DO they come from? Again, no storks involved, Expressions come from static methods on the Expression base class. To create a BinaryExpression that adds 2 numbers, here's the static method on Expression you need:
public static BinaryExpression Add(Expression left, Expression right);
The problem with this however is that you need to have left and right ready before you can create the BinaryExpression. By having our own abstract syntax tree, we can first construct that any way we like and then convert it into a Linq Expression tree by traversing it depth first. When we hit the leaves and come back up, we'll have the operands we need ready and we can create the Linq Expression tree bottom up.
Here's the code on the OperatorNode of our syntax tree that does just that. This code kills two birds with one stone: First, it rewrites our tree so every operator only has two operands. It does that by recursing down and inserting nodes where needed. Then, on the way back up, it creates Linq.Expression nodes from that binary tree and returns the whole expression, rewritten as a Linq Expression.
The reason the two are combined here is that they fit together very nicely since they both use depth first recursion to walk the tree. First converting our own syntax to a binary tree and then convert that to a Linq tree would just be double work. Here it is:.
private Expression ToExpressionInternal(int Child) {
if (Child == Operands.Count - 1) {
return Operands[Child].ToExpression();
} else {
Expression left = Operands[Child].ToExpression();
Expression right = ToExpressionInternal(Child + 1);
switch (Operator) {
case '+': return Expression.Add(left, right);
case '-': return Expression.Subtract(left, right);
case '*': return Expression.Multiply(left, right);
case '/': return Expression.Divide(left, right);
default: throw new Exception();
}
}
}
Let me talk you through a simple case where the operator has 2 operands.
- The code gets called externally for the first time with
Child = 0, to deal with the first operand. - This means that (
0 == 2 -1) is false and it goes into the 'else' branch. Child 0 is put into the left operand. - To work out the righthand operand, the function calls itself with
Child + 1.
- (
1 == 2 - 1) is true, so it goes into the true branch - The second operand is returned as an
int node
- The right hand operand now is that
Int node - Both get put into a
BinaryExpression when we call return Expression.Add(left, right);
For three and more operands, it will keep nesting the expressions into the righthand operand until it has turned them into a binary tree. This is better watched in the debugger than written out here, it wouldn't make a lot of sense writing that down.
When there are no more nodes to go down the tree, the right hand operand is assigned, and both get put into a BinaryOperator which is returned. For deep trees, this will return to where the recursive call was made. For the top node, the complete Linq.Expression is returned. Et voila, the tree, nicely converted!
Compiling and Executing our Linq Expression
We're almost there! Now all we need to do is put our expression into a lambda, and compile and execute that. Randomly punching some knobs on my laptop resulted in this little snippet:
Expression eExpression = nExpression.ToExpression();
Expression<Func<int>> lExpression = Expression.Lambda<Func<int>>(eExpression);
Func<int> fExpression = lExpression.Compile();
The first step calls the code we described above and converts our syntax tree into a Linq Expression tree. Then we put that into a lambda expression. The expression defines what needs to be done, but the lambda lets you actually do that. That's what the lambda does, it's the boilerplate stuff that lets call your expression trees. It handles stuff like parameters. When we have that Lambda, we call Compile() on it, that returns a Func<int>.
Func<int> is shorthand for a delegate int. So now we have a delegate that we can call to execute our expression. After all this work, it would be silly not to, so here goes:
MessageBox.Show(fExpression());
Using the Code
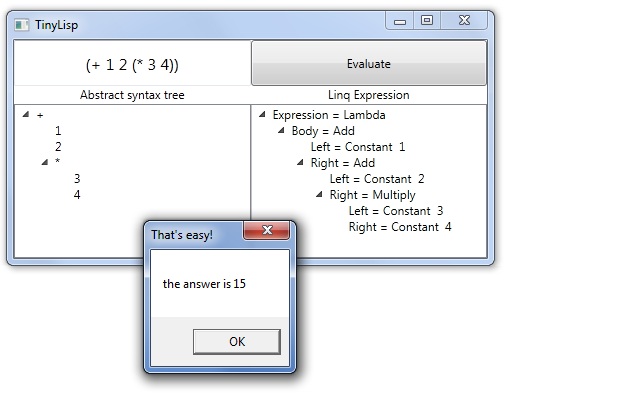
Using the program is pretty easy. When you run it, you can enter an expression in the textbox on the left and press the button. The program will then parse that expression, convert it to a Linq Expression tree and execute that. It also displays the two expression trees side by side, so the user can compare the approaches. Just set a breakpoint on button_click and step through the whole parser en conversion routines should give you a good start on parsers and syntax trees.
Here are a few sample expressions to get you started:
(+ 1 2 3) see how the prefix expression can have any
number of operands, where the Linq tree has only
two and needs to be nested
(+ 5 (* 4 3) (/ 2 1)) the expression we used as example
(+123(*456)) see tree rewriting in action again
(+123456789) really see how binary expression are a pretty blunt tool.
Also note that the digits are seen as separate numbers,
not one large number. The parser only looks at separate chars.
(+ 1 2 (* 3 4)) an expression with a subexpression
(+(-(*(/12)34(*56))7)(+89)1)2) some deep expression
That's all folks. I hope you have fun and learn a little playing around with this. If you like it, please let me know in the comments or rate my article.
History
- 12th June, 2010: Initial post
