Introduction
The question about interpolation recently came to me. So I started working on this topic.
I implemented the Polynomial, Lagrange, Newton and natural spline algorithm and started to compare each one to another. And to my great surprise, I found the fancy spline algorithm not to be the best solution in any case. With certain wave shapes, even a polynomial interpolation works better than a spline interpolation.
But first, some words to explain to the algorithms...
Polynomial Interpolation
The polynomial interpolation algorithm builds for n supporting points a polynomial of the degree n like:
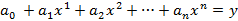
Where x and y are the coordinates of one supporting point. For n supporting points, we get n such equations for x1, y1 to xn, yn. So the algorithm basically has to set up the equation matrix of n*n and solve this by a Gauss algorithm. That gives the parameters a0 to an. With this parameters for any xp the corresponding yp value can be calculated.
The polynomial interpolation is the easiest algorithm to be implemented of the 4. But it gets to its limits regarding accuracy quite soon. If the deltaX between the supporting points is too small or too big, the Gaussian algorithm gets problems with the constellation of the matrix equation already with 10 supporting points. It can help to scale the deltaX up or down to get a deltaX close to 1 only to solve the matrix equation. I made most of the interpolations with deltaX from 0.1 to 0.4. That worked quite well. But the problem remains. With more than 10 supporting points, the polynomial interpolation is not reliable any more. As can be seen in the following graphic:

Trial of a Polynomial interpolation with f=1/x^2 and 20 supporting points. This phenomenon started at 16 supporting points already.
But this is not the end.
In the equation matrix, we start with:

go on to the equation of y2, the y3 and so on. That means in the first line, at the very top, we have the smallest values because of x1 and increasing values further down and Gauss does not like that. Filling the equation matrix upside down like...
 ...
...



...improves the accuracy of the polynomial algorithm quite a bit. Like this, the 20 supporting points can be interpolated correctly with a deltaX of 0.5.
for (i = 0; i < order; i++)
{
m.y[i] = y_k[order - 1 - i];
for (k = 0; k < order; k++)
{
m.a[i, k] = Math.Pow(x_k[order - 1 - i], k);
}
}
...
Just filling the matrix like this instead of:
for (i = 0; i < order; i++)
{
m.y[i] = y_k[i];
for (k = 0; k < order; k++)
{
m.a[i, k] = Math.Pow(x_k[i], k);
}
}
...
Improves the accuracy quite a bit.
Lagrange Interpolation
Lagrange builds a polynomial for each supporting value including the xp value for the interpolation. For n supporting values, that makes n polynomials L1..Ln.

xp is the interpolation variable to which the value yp shall be calculated.
yp becomes now the sum of all the Lk* yk terms.

In the polynomial for Lk can be seen that if xp = xk the polynomial for Lk becomes 1 and yp becomes yk. and the closer xp gets to one of the supporting points, the more weight this point gets.
The interpolation for one interpolation point is made in one loop including the calculation of all the Lk elements and adding the multiplication of Lk * yk together:
for (i = 0; i < order; i++)
{
nominator = 1.0;
denominator = 1.0;
for (k = 0; k < order; k++)
{
if (k != i)
{
nominator = nominator * (xp - x_k[k]);
denominator = denominator * (x_k[i] - x_k[k]);
}
}
if (denominator != 0.0)
yp = yp + y_k[i] * nominator / denominator;
else
yp = 0.0;
}var i = 0;
...
This loop calculates one yp interpolation value.
The Lagrange Algorithm is much more reliable than the Polynomial if the number of supporting points exceeds 10. It also gets its problems with small a deltaX. But 60 supporting points with a deltaX = 0.1 can be interpolated without problems.
Newton Interpolation
Newton uses another polynomial for the interpolation of yp.


The coefficients b0 to bn he calculates like:





In this form, the calculation is not too obvious. But if we put the |XkXk-1|… terms into a table (here for n = 4), things become clearer.

We first have to calculate the |XkXk-1| terms. From this the |XkXk-1Xk-2|…terms and so on. Even though we only need the value on the very top of each column for b0 to b4, we have to calculate all the elements. It seems quite complicated. But in a recursive function, it becomes quite simple.
void CalcElements(double[] x, int order, int step)
{
int i;
double[] xx;
if (order >= 1)
{
xx = new double[order];
for (i = 0; i < order-1; i++)
{
xx[i] = (x[i + 1] - x[i]) / (x_k[i + step] - x_k[i]);
}
b[step - 1] = x[0];
CalcElements(xx, order - 1, step + 1);
}
}
This function is called with the array containing the supporting points, the number of supporting points as the order and it starts with the first step.
Now one yp interpolation value can be calculated like:
for (i = 1; i < order; i++)
{
tempYp = b[i];
for (k = 0; k < i; k++)
{
tempYp = tempYp * (xp - x_k[k]);
}
yp = yp + tempYp;
}
The Newton Algorithm is quite insensitive to a small deltaX and works really fine till 60 supporting points with a deltaX=0.001. I think it is the best of these 3 algorithms.
For more complex problems, the interpolation with natural splines is meant.
Natural Splines
For the spline interpolation, one interpolation function is calculated for each interval between two supporting points.

For each of these intervals, one cubic polynomial is calculated like:

for one interval starting at xi and ending at xi+1 and x as the interpolation variable.
To make sure that the wave shapes of all these intervals fit together, there are some conditions to be fulfilled:
 for i = 1 to n-1
for i = 1 to n-1
 for i = 2 to n-1
for i = 2 to n-1
 for i = 2 to n-1
for i = 2 to n-1
 for i = 2 to n-1
for i = 2 to n-1
From this conditions and the substitution hi = xi+1 - xi the parameters a, b, c and d can be derived:
From condition a, we get ai = yi.
From b, we get:

And c yields:

These two equations put together lead to a matrix equation of the order n-2 for ci with the matrix...

...and the solution vector...

This matrix equation solved by a Gauss algorithm yields c2 to cn-1. The first and the last c both are set as 0.
Now there is only di left and this we get from condition d:

With these parameters, each of the intervals between the supporting points can be interpolated now and at the end, the pieces have to be put together to one graph.
The natural spline algorithm works fine till 100 supporting points. Then it gets its problems with accuracy. But it is surely the most complicated algorithm to be implemented.
Speed improvement for Splines
To calculate the h parameters we have to solve a matrix equation of following structure:
| x1
| x2
| x3
| x4
|
|
| a1
| b1
|
|
| = d1
|
| c2
| a2
| b2
|
| = d2
|
|
| c3
| a3
| b3
| = d3
|
|
|
| c4
| a4
| = d4
|
Matrix equation for n = 4
This is a tridiagonal matrix (at least as long as we don’t want to interpolate a periodic function). This special case of a matrix equation can be solved much quicker than by using Gauss by transforming the A matrix of the equation Ax = D into a left triangular matrix and a right triangular matrix as A = LR.
| a1
| b1
|
|
|
| 1
|
|
|
|
| m1
| r1
|
|
|
| c2
| a2
| b2
|
|
| l1
| 1
|
|
|
|
| m2
| r2
|
|
|
| c3
| a3
| b3
| =
|
| l2
| 1
|
| *
|
|
| m3
| r3
|
|
|
| c4
| a4
|
|
|
| l3
| 1
|
|
|
|
| m4
|
Comparison of the parameters gives:
|
| a1 = m1
| b1 = r1
|
| c2 = l1 * m1
| a2 = l1 * r1 + m1
| b2 = r2
|
| c3 = l2 * m2
| a3 = l2 * r2 + m2
| b3 = r3
|
| c4 = l3 * m3
| a4 = l3 * r3 + m3
| b4 = r4
|
And from this:
li = ci+1 / mi
mi+1 = ai+1 – li * bi
for i = 1 to n-1
To solve this equation we first extend the equation LRx = D by y and say LRxy = Dy (y is not the solution vector of the very top equation). This can be separated to Ly = D and Rx = y.
Ly = D looks like
| 1
|
|
|
|
| y1
|
| d1
|
| l1
| 1
|
|
|
| y2
|
| d2
|
|
| l2
| 1
|
| *
| y3
| =
| d3
|
|
|
| l3
| 1
|
| y4
|
| d4
|
And resolving Ly = D gives
| y1 = d1
|
|
| y1 * l1 + y2 = d2
|
|
| y2 * l2 + y3 = d3
|
|
| y3 * l3 + y4 = d4
|
|
Rx = y looks like
| m1
| r1
|
|
|
| x1
|
| y1
|
|
| m2
| r2
|
|
| x2
|
| y2
|
|
|
| m3
| r3
| *
| x3
| =
| y3
|
|
|
|
| m4
|
| x4
|
| y4
|
And resolving Rx = y gives
| x1 * m1 + x2 * r1 = y1
|
|
| x2 * m2 + x3* r2 = y2
|
|
| x3 * m3 + x4 * r3 = y3
|
|
| x4 * m4 = y4
|
|
With this we basically have to implement 3 loops to solve the tridiagonal Matrix equation:
First loop:
m1 = a1
For i = 1 to n-1
li = ci+1 / mi
mi+1 = ai+1 – li * bi
Second loop:
y1 = d1
for i = 2 to n
yi = di – li-1 * yi-1
Third loop:
xn = yn / mn
For I = n-1 to 1
xi = (yi - bi * xi+1)/mi
Now the first and second loop can be implemented in one if we separate the first term of the first loop and the last term of the second loop
m1 = a1
l1 = c2 / m1
m2 = a2 – l1 * b1
For i = 2 to n-1
li = ci+1 / mi
mi+1 = ai+1 – li * bi
yi = di – li-1 * yi-1
yn = dn – ln-1 * yn-1
So there remain 2 loops to solve the entire matrix equation and that takes a bit more than half as much calculation time as a Gaussian algorithm.
I impelemnted this algorythm in the sample project Splien_LR ind the function SolveLR() :-)
Comparison
The comparison of these 4 algorithms was a little surprising. The Polynomial, the Lagrange and Newton algorithm tend to overshoot in certain conditions. That’s written everywhere. And that’s true. As long as the supporting point values jump up and down, the interpolated wave does it even more. As can be seen at a sample shape of 6 supporting points:
| y
| 0.5
| 11.7
| 14.8
| 4.0
| 2.2
| 0.2
|
| x
| 0.1
| 0.2
| 0.3
| 0.4
| 0.5
| 0.6
|

All 3 algorithms show some overshooting.
The spline interpolation yields a much better result:

A shape I found in a book was 4*exp-(x-0.4)^2.
| y
| 0.0005
| 0.073
| 1.472
| 4.0
| 1.472
| 0.073
| 0.0005
|
| x
| 0.1
| 0.2
| 0.3
| 0.4
| 0.5
| 0.6
| 0.7
|
Seems really to be too much for the Polynomial, Newton and Lagrange algorithm:

And the spline algorithm handles it much better:

The spline curve tends to approach the supporting points more straight and to bend in a smaller radius. That looks quite good. But it is not the best solution for all cases.
A wave shape like 1/x with the points:
| y
| 1.0
| 0.5
| 0.3333
| 0.25
| 0.2
| 0.1666
| 0.143
| 0.125
|
| x
| 0.1
| 0.2
| 0.3
| 0.4
| 0.5
| 0.6
| 0.7
| 0.8
|
Becomes quite different:

Here the Polynomial, Newton and Lagrange algorithm make a smooth, round shape. And what does the spline do?

Great surprise: That’s more like a banana shape.
So let’s go a step further and look at 1/x^2.
| y
| 1.0
| 0.25
| 0.111
| 0.0625
| 0.04
| 0.0277
| 0.0204
| 0.0156
|
| x
| 0.1
| 0.2
| 0.3
| 0.4
| 0.5
| 0.6
| 0.7
| 0.8
|

Again a smooth shape from Polynomial, Newton and Lagrange.
And the spline curve:

O.k. it’s not like a banana anymore. :)
Using the Code
I implemented all 4 algorithms as much the same as possible. There is a global const “order” defining the number of supporting points. This number can be set to an arbitrary value. There are 10 input fields for the y value and 10 for the x value of the supporting points. As long as the order is smaller or equal to 10, these fields are editable and the supporting points can be manipulated. If orders bigger than 10 should be tested, the supporting values have to be set in the software (I kept the code as simple as possible). The supporting points are implemented in the arrays x_k and y_k and the interpolated wave is put in the arrays xp and yp containing “datapoints” elements. The global const “deltaX“ might be clear. But it's not a must to use it. The x_k values can be defined free.
The wave shape is drawn in the panel pGraph by the function DrawGraph(int maxPoints, double minX, double maxX, bool doClear). This function scales the graphic to fit into the panel and clears the panel before drawing if doClear is true.
The calculation is done in the button1_Click event.
Points of Interest
It really depends quite a lot on the wave shape that should be interpolation which algorithm is best and it might be wise to compare the algorithms and to have a look at the interpolated shape. For small numbers of supporting points, the simple Polynomial algorithm might be the best solution. But already at the amount of 10 supporting points, a Lagrange or Newton Algorithm should be used whereas the Newton should be preferred. The spline algorithm is quite fancy but it’s not always worthwhile to use it as it is quite complicated to be implemented and not too clear to be debugged (just in case :-)).
For more detailed descriptions visit www.mosismath.com :-)
