A Brief Test on the Efficiency of a .NET 4.0 Parallel Code Example

• Download source - 1.33 KB

Introduction

In a previous article, I introduced a series of brief tests on the calculation efficiency of a piece of CUDA code and another piece employing the thrust library. In the tests, a summation of squares of an integer array (random numbers from 0 to 9) was performed and the code execution efficiency was recorded. The conclusion is, briefly, the parallelism on a GPU chip shows great potential, especially for those containing whopping number of parallel elements.

However, on the other hand, the computer, on which I performed the tests, also bears an Intel Q6600 quad-core CPU. Obviously the single thread plain loop code cannot utilize the full potential of the multi-core CPU. Therefore, I wrote some pieces of C# code to re-perform the summation operation of squares, and by comparing the efficiency of the different parallel algorithm strategies, I conclude some helpful points which might be interesting for those developers working on similar topics.

[This article can be regarded as a piece of accompanying work of the article, "A brief test on the code efficiency of CUDA and thrust".]

Background

The serially executed plain loop (to compute the summation of squares) is the baseline of the benchmark work. Not surprisingly, the code in C# is written as:

var watch = Stopwatch.StartNew();

int final_sum = 0;
for (var i = 0; i < DATA_SIZE; i++)
{
    final_sum += data[i] * data[i];
}

watch.Stop();
elapsed_time = (double)watch.ElapsedMilliseconds / 1000;

in which data is an in-advance generated array with DATA_SIZE of random integers.

// generate random number ranged in [0, 9]
static void GenerateNumbers(int[] number)
{
    Random ro = new Random();
    for (var i = 0; i < number.Length; i++)
    {
        number[i] = ro.Next(0, 9);
    }
}

System.Threading.Tasks.Parallel in .NET 4.0

I chose C# because of my familiarity with the language. Another important reason is the new support upon parallel programming in the recently released Visual Studio 2010 and .NET 4.0. Since loads of information can be found about the feature, such as the article "Introducing .NET 4.0 Parallel Programming" on CodeProject, I don't write redundant words but only give the corresponding code to do my calculation.

With the help of the new System.Threading.Tasks namespace provided by .NET 4.0, the for loop is replaced with a call to a method namely System.Threading.Tasks.Parallel.For. It is a static method. A anonymous function delegate defines the real work, which actually corresponds to the code block written inside the previous plain for loop. A thread pool is commonly used to incubate the threads to implement the work; however, we fortunately don't need to know any details, as the Tasks namespace looks after everything. Finally, the practical code is:

final_sum = 0;
Parallel.For(0, DATA_SIZE, i =>
{
    Interlocked.Add(ref final_sum, data[i] * data[i]);
});

The add work is then parallelised. Another point to note is that Interlocked.Add method is used to make the add operation, previously final_sum += data[i] * data[i];, thread-safe.

That's all. It is simple, isn't it? However, using my quad core CPU the parallel code didn't show any advantages. For example, if managing 1 M (1 M equals to 1 * 1024 * 1024) integers, the serial code used 7 ms but the parallel code consumed 113 ms, which is 15 times longer.

Why? :( Then comes the interesting point.

Points of Interest

Do remember we used the Interlocked.Add method to lock the shared resources final_sum among the threads allocated. (data[i] doesn't matter because each thread only accesses one element of the array and these elements are different from a thread to another.) This is critical to consider about the code execution efficiency, since all threads have to wait for the access to final_sum in a queue. In other words, the access to final_sum is still serial, although the code is parallelised. That is basically why the code execution time was not reduced. Furthermore, because of the overhead taken to allocate and manage threads, the execution time is even much more.

Thinking about the parallel algorithm used for the same purpose in my CUDA program, we actually don't need to parallelise the summation operation down to each single element of the array. A suggested way is supposed to be dividing the array into a certain number of pieces. Each piece contains an equal number of elements and the elements from different pieces don't overlap. Theoretically, we can employ a number of threads, set up the one-to-one correspondence between the threads and the pieces, and then:

1. Calculate the sub-summation in each piece by its corresponding thread and record the result
2. Do a summation of all the sub-summation results

If split the array into 1 k (1 k equals to 1 * 1024) pieces, i.e. the thread number is also 1 k, the practical code might be:

// initial value for thread number
long THREAD_NUM = 1024;

// buffer for the threads
int[] result = new int[THREAD_NUM];
// piece size for each thread
long unit = DATA_SIZE / THREAD_NUM;

watch.Restart();

Parallel.For(0, THREAD_NUM, t =>
{
    for (var i = t * unit; i < (t + 1) * unit; i++)
    {
        result[t] += data[i] * data[i];
    }
});

final_sum = 0;
for (var t = 0; t < THREAD_NUM; t++)
{
    final_sum += result[t];
}

watch.Stop();
elapsed_time = (double)watch.ElapsedMilliseconds / 1000;

In the CUDA version, I used 16 k threads to do the calculation. How to determine a proper thread number for the quad core CPU to obtain a best performance? I did a sensitivity study on this. I used TN, namely Thread Number, equal to 1 k, 16 k and 256 k, respectively, and tested the code execution times; the recorded values (unit: second) are listed in the table below:

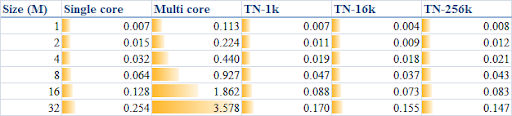
The table also lists the consumed times by the serial code and the parallel code without splitting the array. Briefly, the descriptions of the items are:

• Single core: Execution time of the serially executed plain loop
• Multi core: Execution time if using the method System.Threading.Tasks.Parallel.For without splitting the array into pieces
• TN-1k: Execution time if splitting the array data into 1 k groups and using Parallel.For method to manage them. In each group, an internal plain loop is employed to compute the sub-summation
• TN-16k: Same with the former, but separating the array into 16 k groups
• TN-256k: Same with the former, but separating the array into 256 k groups

The corresponding trends can be summarized as:

or compare them by the histogram:

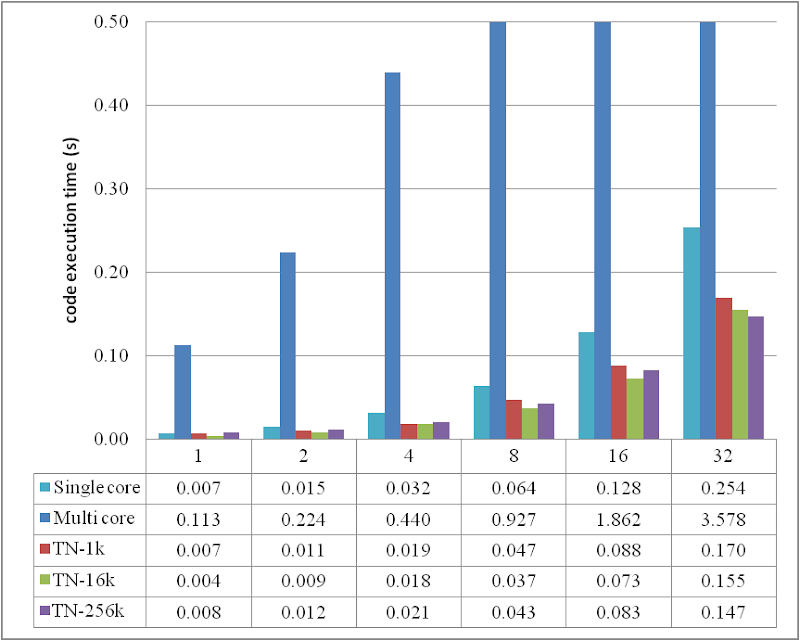
After grouping the data into a certain number of parallel units, the execution performance was dramatically improved, and the improved performance is already better than the serially executed loop, although the improvement did not reach 4 times as my quad core processor.

The figures also reveal that it is not ideal to use only 1 k threads. 16 k is better for most scenarios except when DATA_SIZE = 32 M. This probably implies that, for much more data, more threads might be needed to handle them.

Conclusion

The original purpose for me to perform the test is to compare the CUDA calculation efficiency with the multi-core efficiency. However, in the process, I released the port from a serial loop to a parallel code is not as simple as replacing the for loop by using a Parallel.For method, although which was expected. In practice, like designing the CUDA program, thread numbers have to be carefully considered.

Based on the test, I found that, for 1 M to 32 M integers, using 16 k threads can achieve a very much balanced performance. Although for DATA_SIZE = 32 M the efficiency of 16 k threads is less than that of 32 k threads, the loss is around 5%.

Moreover, by comparing these C# results with the CUDA result from the previous article, I also found that:

• With respect to the serial code, i.e. the plain loop code, the C++ code performed better than the C# code; both code were run on the same Q6600 CPU.
• The CUDA code performed better than the parallel C# code, even though both employed 16 k threads. The CUDA was run on a 9800 GTX+ chip and the C# code was run on a Q6600 processor.

We know, when using CUDA the memory transfer between the CPU and the GPU costs very much. Even though the memory transfer overhead, the CUDA code still performs better than a piece of parallel C# code which utilizes the 4 cores of a CPU at 2.40 GHz. At least for this summation of squares calculation, this is true. Does this imply that CUDA does bring great potentials to us?

Code Instruction

The code file ParallelExample.cs, contained in the zip package, includes the test code for serial and parallel methods with different policies, as mentioned in the present article. Note that the calculation execution has to be repeated for enough times in order to extract average values for a practical benchmark test; for clarity and simplification. I didn't include this feature in the code attached, but it is surely easy to be added.

The code was built and tested in Windows 7 32 bit plus Visual Studio 2010. The test computer specification is basically Intel Q6600 quad core CPU plus 3G DDR2 800M memory. Although the hard drive used is not good, (marked 5.1 by Windows 7), I don't think it plays an important role in the test.

History

• 01/07/2010: The first version of the present article was released.