Data Structures for Polynomial Division

• Download source - 34 KB

This article deals with the implementation of polynomial division by the familiar algorithm of long integer division in the context of two applications. The first application involves the computation of an index into a hash table, and the second involves the computation of cyclic redundancy check codes. The data structures for polynomial division are described after a brief description of the two applications.

Hashing by Polynomial Division

A hashing technique based on algebraic coding theory uses polynomial division to compute the index into the hash table (cf. Knuth, D. The Art of Computer Programming, Vol. 3: Sorting and Searching. Boston, Massachusetts: Addison Wesley, 1973, pp. 512-513; Second Edition, 1998, p. 520). The table size \(m\) is assumed to be a power of two, that is, , for some \(m > 1\). In order to hash a key into the table, this technique uses an m^th-degree polynomial

which for \(x = 2\) can be interpreted as the binary representation of an integer.

The key to be hashed is assumed to be a \(q\)-character string. The ASCII codes of the string make up a sequence of bits, which is nothing but an \(n\)-bit (\(n = 8q\) binary number. Such a number can also be interpreted as a polynomial in \(x\):

The hash index into the table is obtained as the remainder of the polynomial division \(x^mK(x) mod P(x)\) using arithmetic modulo 2. The multiplication \(x^mK(x)\) amounts to shifting the bits of the key \(m\) positions to the left, and the remainder of the division is the polynomial

which represents the \(m\)-bit binary number \(h_{m-1}...h_1h_0\). This number is a proper index into the table because for a table size of \(2^2\), the indices range from 0 to \(2^m-1\) and each index is encoded in binary with exactly \(m\) bits.

As an illustration, consider a key whose binary encoding is 110100110111. The binary number has a polynomial representation

Suppose now that this key is to be indexed into a hash table of size \(2^5\) (32 elements, with index range spanned by 5-bit numbers 00000 to 11111), and that the divisor polynomial is chosen to be

In modular arithmetic, we are not interested in the quotient, but only in the remainder of the long division \(x^mK(x) mod P(x)\). Hence, the division is achieved using \(\oplus \) for subtraction without borrow, as shown below:

11010011011100000
110101
------
00000111011100000
     110101
     ------
     001110100000
       110101
       ------
       0011110000
         110101
         ------
         00100100
           110101
           ------
           010001

The remainder is equal to 10001 and the integer equivalent (17) is the index into the hash table for the key in question.

The most difficult problem to address in hashing is the avoidance of collisions, and a judicious choice of the hashing function is of prime importance. In the case of hashing by polynomial division, the divisor polynomial determines the effectiveness of the method. Knuth has noted that for keys consisting of 15 bits, the 10^th-degree divisor polynomial yields different remainders for any pair of keys that differ in fewer than seven bit positions.

Computation of Cyclic Redundancy Check (CRC) Codes

CRC codes are used in data transmission both between computers over communications lines, and between hard drives and the CPU to detect burst errors (cf. Ercegovac, M.D., and T. Lang Digital Systems and Hardware/ Firmware Algorithms. New York: Wiley, 1985, pp. 744-745). A burst is defined to be a large chunk of data transferred at high speed.

A CRC code consists of \(k\) data bits (or message bits) and \(r < k\) check bits. The check bits are obtained as the remainder of the division of a data bit-vector and a generator bit-vector. To reduce the complexity of the division operation, subtractions are performed in a bitwise fashion and without borrow. Thus, if \(X=x_{n-1}x_{n-2}...x_1x_0\) and \(Y=y_{n-1}y_{n-2}...y_1y_0\) denote two bit-vectors of length \(n\), the subtraction \(X-Y=D=d_{n-1}d_{n-2}...d_1d_0\) is performed bit by bit, where \(d_i=x_i\oplus y_i\) for \(0\leq i< n\).

Since the bits of binary numbers equal the coefficients of a polynomial in 2, a \(k\)-bit message can be thought of as a polynomial in \(x\), \(M(x)\), of order \(k\) – 1. Similarly, to obtain an \(r\)-bit CRC check vector a generator polynomial in \(x\), \(G(x)\), of order \(r\) can be used. Specifically, the message polynomial \(M(x)\) is divided by the generator polynomial \(G(x)\) so that

where \(Q(x)\) is the quotient polynomial, and \(R(x)\) is the remainder polynomial obtained through a process similar to long integer division. The quotient polynomial is discarded, and the remainder polynomial is the CRC code for the message. For the purposes of data transmission, a coded message is formed by appending the CRC code to the message. The coded message can also be viewed as a polynomial in \(x\), and is defined as

The effect of errors in data transmission is described formally as follows. Let \(E(x)\) denote an error polynomial, which is a bit-vector having 1 at the bit positions of the message that are modified (flipped) by the error, and 0 at the bit positions that remain unchanged. The error modifies the coded message into a polynomial of the form

This erroneous coded message models the effect of noise in the communications line, and represents the received message.

To verify the occurrence of a transmission error, the received message is divided by the same generator polynomial \(G(x)\). Performing the operation mathematically,

the final result obtained is due to the self-cancellation property of the exclusive-or operator. Since the quotient polynomial is of no interest, a transmission error is detected if the remainder of the division \(E(x) / G(x)\) is different from a zero bit-vector, meaning that \(E(x)\) is not divisible by \(G(x)\). The generator polynomial is chosen to detect all burst errors of length less than the degree of the polynomial. Common generator polynomials are of degree 16 or 32.

As an illustration, consider a variation on the example for hashing by polynomial division. A system is to process 12-bit messages with a generator polynomial of degree 5 (CRC-5), defined as

The message to be transmitted is 110100110111 and has a polynomial representation

The CRC code for the message is computed by long division, using \(\oplus \) for subtraction without borrow:

11010011011100000
110101
------
00000111011100000
     110101
     ------
     001110100000
       110101
       ------
       0011110000
         110101
         ------
         00100100
           110101
           ------
           010001

yielding a remainder equal to 10001. Hence the coded message would be 11010011011110001.

Suppose now that a transmission error changes three consecutive bits of the coded message, as described by the error vector 00001110000000000. The resulting erroneous coded message is 11011101011110001 and division by the generator polynomial yields a non-zero remainder, so the error is detected. On the other hand, if an error such as 00101111100000000 changes five or more bits, the erroneous message would be 11111100111110001, and division by the generator polynomial would yield a zero remainder, with the consequence that the error would go undetected.

Eight-Bit Shift Registers

The computations of a hash index and of a CRC code by polynomial division are two aspects of the same problem. Both computations are usually implemented in hardware by means of shift registers, but it is possible to define a set of data structures to efficiently implement polynomial division in software. The first step involves defining a class to model (i.e., simulate) the operation of a basic shift register. Consider modeling a generic, combinational 8-bit shift register having the following hardware block diagram and functional specification.

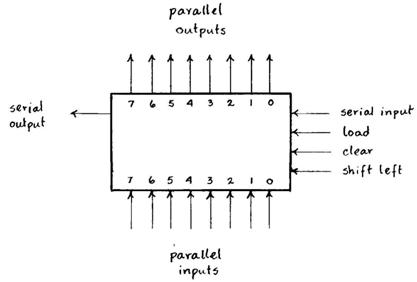
The register has eight parallel input bits (\(i_7...i_0\)), eight parallel output bits (\(o_7...o_0\)), one serial input bit (\(s_{out}\)), one serial output bit () and three command inputs (load, clear, and shift left). If the clear signal is activated, bits \(o_7...o_0\) are all set to zero. If the load signal is activated, bits \(i_7...i_0\) are copied to bits \(o_7...o_0\). If the shift left signal is activated, the register shifts its bits one position to the left: \(s_{out}\leftarrow o_7,o_{k+1}\leftarrow o_k\) , (for \(0\leq k< 7\)), and \(o_0\leftarrow s_{in}\). The \(s_{in}\) and \(s_{out}\) lines allow connecting several registers in cascade. The output bits \(o_7...o_0\) can be read at any time.

To model in software a hardware shift register, a C# class can be defined to represent the register’s bits as a private data member, and to implement its operations by means member functions. (Hereafter, all the C# classes will be assumed to reside in the PolynomialDivision namespace, and all the code will be assumed to run in the context of a console application.)

public class _8bitShiftRegister
{
   private byte data; // register's data bits

   public _8bitShiftRegister()
   {
      data = 0x00;
   }

   public _8bitShiftRegister( byte _data )
   {
      data = _data;
   }

   public byte Data
   {
      get { return data; }
      set { data = value; }
   }

   public void Load( byte _data ) // "Load" command (signal)
   {                              // "parameterized" version of Data.set
      data = _data;
   }

   public byte Read() // "Read" command (signal)
   {                  // "parameterized" version of Data.get
      return data;
   }

   public void Clear() // "Clear" command (signal)
   {
      data = 0x00;
   }

   public byte ShiftLeft( byte SerialIn ) // "Shift left" command (signal)
   {
      byte SerialOut = (byte)( data >> 7 );

      data <<= 1; // shift left 1 bit
      if ( SerialIn != 0x00 )
      {
         data |= 0x01;
      }
      return SerialOut;
   }

   public void Divide( _8bitShiftRegister source ) // "Divide" command
   {
      data ^= source.Data; // modulo 2 division via bitwise xor operator
   }

   public void Print( NL nl = NL.no )
   {
      Console.Write( String.Format( "{0:x2}", data ) );
      if ( nl == NL.yes )
      {
         Console.WriteLine();
      }
   }

   public void SelfTest()
   {
      byte sIn = 0;
      int i;

      Console.WriteLine( "Self-test 1\n" );

      data = 0xff;
      Print( NL.yes );

      for ( i = 0; i < 8; ++i )
      {
         byte sOut;

         sOut = ShiftLeft( sIn );
         Console.WriteLine(
            String.Format( "{0} <-- {1:x2} <-- {2}", sOut, data, sIn ) );
      }
      Console.WriteLine();

      Console.WriteLine( "Self-test 2\n" );

      sIn = 0x01
      data = 0x00;
      Print( NL.yes );

      for ( i = 0; i < 8; ++i )
      {
         byte sOut;

         sOut = ShiftLeft( sIn );
         Console.WriteLine(
            String.Format( "{0} <-- {1:x2} <-- {2}", sOut, data, sIn ) );
      }
      Console.WriteLine();
   }
}// _8bitShiftRegister (class)

The member functions Load, Read, Clear and ShiftLeft of class _8bitShiftRegister constitute a straightforward implementation of the behavioral specification of the register. Function Divide was defined in preparation for the use of this basic data structure in the implementation of polynomial division. It implements 8-bit division in modulo 2 arithmetic by means of the bit-wise exclusive-or operator. Similarly, functions Print and SelfTest are not part of the register’s specifications but are convenient for simulation purposes. The self-testing capability of the class can be exercised by the following program.

class Program
{
   static void Main( string[] args )
   {
      _8bitShiftRegister reg = new _8bitShiftRegister();

      reg.SelfTest();
   }
}// Program (class)

The execution of this program produces the following output in a command prompt window (shown in two-column format here).

Self-test 1   ff 1 <-- fe <-- 0 1 <-- fc <-- 0 1 <-- f8 <-- 0 1 <-- f0 <-- 0 1 <-- e0 <-- 0 1 <-- c0 <-- 0 1 <-- 80 <-- 0 1 <-- 00 <-- 0

Self-test 2   00 0 <-- 01 <-- 1 0 <-- 03 <-- 1 0 <-- 07 <-- 1 0 <-- 0f <-- 1 0 <-- 1f <-- 1 0 <-- 3f <-- 1 0 <-- 7f <-- 1 0 <-- ff <-- 1

The first test loads 0xff into the register, sets the serial input to 0 and shifts left eight times. The second test loads 0x00 into the register, sets the serial input to 1 and shifts left eight times. The format for the program’s output is serial-out <-- data-bits <-- serial-in. As the reader can verify the results are as expected.

Polynomial Division Using a Shift Array

In order to implement polynomial division by shifting bits, the _8bitShiftRegister class can be used as the basic data structure for a shift array. Instead of shifting right the divisor under the dividend as it is done by hand when performing long integer division, the dividend can be shifted over the divisor. If the dividend is stored in an array of 8-bit shift registers, then the left shifting of the array is a simple task.

To be able to divide the prefix of the dividend by the divisor, there must be a means of referring to a section of the shift array by name in order to manipulate it explicitly, which can be accomplished with a C/C++ union to name the prefix of the shift array. (The values of mArg and mChars are unimportant at this point.)

union {
   _8bitShiftRegister arg[ mArg ];            // argument to generator polynomial
   _8bitShiftRegister chars[ mChars + mArg    // character buffer
                                    + mArg ]; // + area to append zeros
} AC;

C# does not have a union data type. However, the System.Runtime.InteropServices namespace has the functionality to emulate unions with structs as follows.

[StructLayout( LayoutKind.Explicit, Size = 8 )]
struct Union
{
   [FieldOffset( 0 )]
   public _8bitShiftRegister[] arg;   // argument to generator polynomial
   [FieldOffset( 0 )]
   public _8bitShiftRegister[] chars; // character buffer (dividend) + area to append zeros
}// Union

This information was obtained from James Kovacs on a web page from the Microsoft Developer Network. (Using the search string “Union in C#” in Google, the first link titled “C# equivalent to C union” leads to his article.) It is important to realize that the Union just defined is a type, not a variable.

Assume that the polynomials to be manipulated will have a maximum degree of 31, thus requiring a 32-bit representation, and that the dividend will always be represented by a multiple of eight bits. Hereafter, all the variables and functions will be data members and methods, respectively, of the class ShiftArray. I will describe only the most important methods. (The complete code is in file ShiftArray.cs). The data members are defined, and explained by comments, as follows.

private _8bitShiftRegister[] poly, // divisor polynomial
                             mask; // mask used by function ShiftLeftToMSb

private Union AC;

private uint uiPoly,  // uint equivalent of poly
             uiMask;  // uint equivalent of mask

private uint[] uiDmask; // masks used to print a polynomial

private int nBits,    // # of bits in AC.chars
            nBytes,   // # of bytes in AC.chars == ceiling( nBits / 8 )
            cBits,    // current # of bits in AC.chars
            cBytes,   // current # of bytes in AC.chars
            divMSb,   // most significant bit of divisor polynomial
            pBits,    // degree (# of bits) of divisor polynomial
            quot,     // quotient of divMSb / 8
            max,      // maximum print position for AC.chars
            mMessage; // # of characters in message

private byte[] message; // copy of message in AC.chars

The constructor allocates space for all the arrays and initializes the data members using the constants defined in file Cnst.cs. It then calls function GenerateBitMasks to initialize an array of bit masks used to print polynomials, and then function InitPolyAndMask to initialize the generator polynomial and the mask for the most significant bit to be used when shifting to the left.

public ShiftArray( int pOf2, uint uiP, int msb )
{
   int i;

   poly = new _8bitShiftRegister[ Cnst.mArg ];   // divisor polynomial
   mask = new _8bitShiftRegister[ Cnst.mArg ];   // mask used by function ShiftLeftToMSb
   AC.arg = new _8bitShiftRegister[ Cnst.mArg ]; // argument to generator polynomial
   for ( i = 0; i < Cnst.mArg; ++i )
   {
      poly[ i ] = new _8bitShiftRegister();
      mask[ i ] = new _8bitShiftRegister();
      AC.arg[ i ] = new _8bitShiftRegister();
   }
   AC.chars = new _8bitShiftRegister[ Cnst.mChars + Cnst.mArg2 ]; // arg/buffer + area to
                                                                  // append zeros and remainder

   for ( i = 0; i < Cnst.nChars; ++i )
   {
      AC.chars[ i ] = new _8bitShiftRegister();
   }
   message = new byte[ Cnst.mChars + Cnst.mArg ];
   cBits = nBits = Util.Min( pOf2, Cnst.mBits );
   cBytes = nBytes = Util.BitsToBytes( nBits );
   max = cBytes + Cnst.mArg;
   divMSb = msb;
   pBits = msb + 1;
   quot = divMSb >> 3;

   Console.WriteLine( "Initializing ShiftArray\n" );
   Console.WriteLine( String.Format( "bits == {0}, bytes == {1}", nBits, nBytes ) );
   Console.WriteLine( String.Format( "generator msb == {0}, bits == {1}\nquot == {2}",
                                     divMSb, pBits, quot ) );
   GenerateBitMasks();
   InitPolyAndMask( uiP );
}// ShiftArray

private void GenerateBitMasks()
{
   uint m = 0x00000001;

   uiDmask = new uint[ 32 ];

   for ( int i = 0; i < 32; ++i )
   {
      uiDmask[ i ] = m;
      m <<= 1;
   }
}

private void InitPolyAndMask( uint uiP )
{
   uint uiM;

   uiPoly = uiP;
   uiMask = ( (uint)1 ) << divMSb;

   uiM = uiMask;
   for ( int i = Cnst.mArg - 1; i > -1; --i )
   {
      poly[ i ].Load( (byte)uiP );
      mask[ i ].Load( (byte)uiM );
      uiP >>= 8;
      uiM >>= 8;
   }
   Console.Write( "Generator polynomial" );
   PrintPolynomial( uiPoly );
   PrintRange( "            MSb mask == 0x", mask, Cnst.mArg );
}// InitPolyAndMask

Before describing more functions, I will deal with function SelfTest (defined in the spirit of the self-test functionality of the _8bitShiftRegister class), which illustrates the whole process of CRC processing. This function drove the development of the code in a top-down fashion.

public void SelfTest()
{
   LoadString( "M.I.T.EE" );
   GenerateCRC();
   PrintCRC();
   VerifyCRC();
}// SelfTest

Function LoadString receives a message as a character string (str), clears the AC.arg section of AC.chars, copies the string into AC.chars after the AC.arg section, makes a copy of the original message for CRC verification purposes, and clears the remaining of AC.chars. It then computes the number of bits and bytes to be processed.

public void LoadString( string str )
{
   int i, j, m, n = str.Length, p;

   m = n > Cnst.mChars ? Cnst.mChars : n; // maximum number of characters to load
   p = m + Cnst.mArg;                     // add size of area to append zeros

   for ( i = 0; i < Cnst.mArg; ++i ) // clear AC.arg section of AC.chars
   {
      AC.chars[ i ].Clear();
   }
   for ( i = Cnst.mArg, j = 0; i < p; ++i, ++j ) // load characters from str
   {
      byte b = (byte)str[ j ];
      AC.chars[ i ].Load( b );
      message[ j ] = b;
   }
   mMessage = j;
   while ( i < Cnst.nChars ) // clear remaining part of AC.chars
   {
      AC.chars[ i++ ].Clear();
   }
   cBits = (n << 3) + divMSb;
   cBytes = Util.BitsToBytes( cBits );
   PrintMessage( "loaded" );
}// LoadString

As explained by the comments in function GenerateCRC, it initially aligns the dividend with the divisor. Then, as long as there are significant bits to process, the function repeatedly applies the divisor polynomial to the dividend and re-aligns the dividend with the divisor. At the end, the remaining bits, which constitute the CRC, are shifted all the way to the left.

public void GenerateCRC()
{
   Console.WriteLine( "\nGenerating CRC\n" );
   Console.WriteLine( "cBits cBytes | arg. |  chars\n" );
   ShiftLeftToMSb( DCR.no ); // align dividend with divisor
   while ( cBits > pBits )
   {
      ArgDivPoly();          // apply divisor polynomial
      ShiftLeftToMSb();      // re-align dividend with divisor
   }
   ShiftLeftToEnd();         // shift remainder all the way to the left
}// GenerateCRC

As far as bit manipulation is concerned, the left-shift functions and function ArgDivPoly are self explanatory and are defined below. Throughout the definitions, observe the use of the _8bitShiftRegister functionality.

public void ShiftLeftToMSb( DCR dcr = DCR.yes )
{
   byte mskByte = mask[ 3 - quot ].Read();

   while ( ( cBits > 0 )
           &&
           ( ( AC.arg[ 3 - quot ].Read() & mskByte ) != mskByte ) )
   {
      ShiftLeft( dcr );
   }
   Print();
}// ShiftLeftToMSb

public void ArgDivPoly()
{
   for ( int i = 0; i < Cnst.mArg; ++i )
   {
      AC.arg[ i ].Divide( poly[ i ] );
   }
   Print();
}// ArgDivPoly

public void ShiftLeftToEnd()
{
   if ( !ZeroArg() )
   {
      Console.WriteLine( "\nShifting AC.arg to end\n" );
      while ( ( AC.arg[ 0 ].Read() & 0x80 ) != 0x80 )
      {
         ShiftLeft( DCR.no );
      }
      Print();
   }
}// ShiftLeftToEnd

private bool ZeroArg() // is AC.arg all 0's ?
{
   bool zero = true;

   for ( int i = 0; i < Cnst.mArg; ++i )
   {
      if ( AC.arg[ i ].Read() != 0x00 )
      {
         zero = false; break;
      }
   }
   return zero;
}// ZeroArg

public void ShiftLeft( DCR dcr )
{
   int i, m = Cnst.mChars + ( Cnst.mArg << 1 );
   byte Cout;

   if ( cBits > 0 )
   {
      Cout = 0;
      for ( i = m - 1; i > -1; --i )
      {
         Cout = AC.chars[ i ].ShiftLeft( Cout );
      }
      if ( dcr == DCR.yes )
      {
         --cBits;
         if ( ( cBits % 8 ) == 0 )
         {
            --cBytes;
         }
      }
   }
}// ShiftLeft

During the generation of the CRC a number of print functions are called for logging purposes. These functions (PrintPolynomial, Print, PrintACarg, PrintACchars, and PrintCRC) are defined in file ShiftArray.cs and, for brevity’s sake, I will not describe them. The output produced in a command prompt window by the generation of the CRC for the sample message is as follows (to save space, it is shown in two column format). The two trailing zeros in the hex representation of the message are not part of it.

Initializing ShiftArray

bits == 64, bytes == 8
generator msb == 5, bits == 6
quot == 0
Generator polynomial == 0x00000035 == x^5 + x^4 + x^2 + 1
            MSb mask == 0x00000020


Message: 'M.I.T.EE' loaded

         4d2e492e542e454500


Generating CRC


cBits cBytes | arg. |  chars

   69      9 000000269724972a1722a28000
   69      9 000000139724972a1722a28000
   68      9 000000272e492e542e45450000
   68      9 000000122e492e542e45450000
   67      9 000000245c925ca85c8a8a0000
   67      9 000000115c925ca85c8a8a0000
   66      9 00000022b924b950b915140000
   66      9 00000017b924b950b915140000
   65      9 0000002f724972a1722a280000
   65      9 0000001a724972a1722a280000
   64      8 00000034e492e542e4545000
   64      8 00000001e492e542e4545000
   59      8 0000003c925ca85c8a8a0000
   59      8 00000009925ca85c8a8a0000
   57      8 000000264972a1722a280000
   57      8 000000134972a1722a280000
   56      7 0000002692e542e4545000
   56      7 0000001392e542e4545000
   55      7 0000002725ca85c8a8a000
   55      7 0000001225ca85c8a8a000
   54      7 000000244b950b91514000
   54      7 000000114b950b91514000
   53      7 00000022972a1722a28000
   53      7 00000017972a1722a28000
   52      7 0000002f2e542e45450000
   52      7 0000001a2e542e45450000
   51      7 000000345ca85c8a8a0000
   51      7 000000015ca85c8a8a0000
   46      6 0000002b950b91514000
   46      6 0000001e950b91514000
   45      6 0000003d2a1722a28000
   45      6 000000082a1722a28000
   43      6 00000020a85c8a8a0000
   43      6 00000015a85c8a8a0000
   42      6 0000002b50b915140000
   42      6 0000001e50b915140000
   41      6 0000003ca1722a280000
   41      6 00000009a1722a280000
   39      5 0000002685c8a8a000
   39      5 0000001385c8a8a000
	cBits cBytes | arg. |  chars

   38      5 000000270b91514000
   38      5 000000120b91514000
   37      5 000000241722a28000
   37      5 000000111722a28000
   36      5 000000222e45450000
   36      5 000000172e45450000
   35      5 0000002e5c8a8a0000
   35      5 0000001b5c8a8a0000
   34      5 00000036b915140000
   34      5 00000003b915140000
   30      4 0000003b91514000
   30      4 0000000e91514000
   28      4 0000003a45450000
   28      4 0000000f45450000
   26      4 0000003d15140000
   26      4 0000000815140000
   24      3 00000020545000
   24      3 00000015545000
   23      3 0000002aa8a000
   23      3 0000001fa8a000
   22      3 0000003f514000
   22      3 0000000a514000
   20      3 00000029450000
   20      3 0000001c450000
   19      3 000000388a0000
   19      3 0000000d8a0000
   17      3 00000036280000
   17      3 00000003280000
   13      2 000000328000
   13      2 000000078000
   10      2 0000003c0000
   10      2 000000090000
    8      1 0000002400
    8      1 0000001100
    7      1 0000002200
    7      1 0000001700
    6      1 0000002e00

Shifting AC.arg to end

    6      1 b800000000

CRC: b8

Function VerifyCRC is used to check that the generated CRC is correct. To this end, the function re-loads the original message, appends the CRC to the message, and calls GenerateCRC again. The result should be a CRC equal to zero.

private void VerifyCRC()
{
   Console.WriteLine( "\nVerifying CRC\n" );
   ReloadMessage();
   AppendCRC();
   GenerateCRC();
   PrintCRC();
}// VerifyCRC

private void ReloadMessage()
{
   // Copy message into AC.chars without
   // altering AC.arg

   for ( int i = Cnst.mArg, j = 0; i < max; ++i, ++j )
   {
      AC.chars[ i ].Load( message[ j ] );
   }
   PrintMessage( "reloaded" );
}// ReloadMessage

private void AppendCRC()
{
   int crcBytes, crcBits, i, j;

   Console.WriteLine( "\nAppending CRC\n" );
   crcBytes = cBytes;
   crcBits = cBits;
   cBytes = nBytes;
   cBits = nBits;
   i = cBytes + Cnst.mArg;
   j = 0;
   while ( crcBytes > 0 )
   {
      AC.chars[ i++ ].Load( AC.arg[ j ].Read() );
      AC.arg[ j++ ].Clear();
      ++cBytes;
      --crcBytes;
      if ( crcBits >= 8 )
      {
         crcBits -= 8;
         cBits += 8;
      }
   }
   cBits += crcBits;
   Print();
}// AppendCRC

The output produced during the CRC verification process is as follows. (Again, the two trailing zeros in the hex representation of the message are not part of it.)

Verifying CRC


Message: 'M.I.T.EE' reloaded

         4d2e492e542e454500


Appending CRC

   70      9 000000004d2e492e542e4545b8

Generating CRC


cBits cBytes | arg. |  chars

   70      9 000000269724972a1722a2dc00
   70      9 000000139724972a1722a2dc00
   69      9 000000272e492e542e4545b800
   69      9 000000122e492e542e4545b800
   68      9 000000245c925ca85c8a8b7000
   68      9 000000115c925ca85c8a8b7000
   67      9 00000022b924b950b91516e000
   67      9 00000017b924b950b91516e000
   66      9 0000002f724972a1722a2dc000
   66      9 0000001a724972a1722a2dc000
   65      9 00000034e492e542e4545b8000
   65      9 00000001e492e542e4545b8000
   60      8 0000003c925ca85c8a8b7000
   60      8 00000009925ca85c8a8b7000
   58      8 000000264972a1722a2dc000
   58      8 000000134972a1722a2dc000
   57      8 0000002692e542e4545b8000
   57      8 0000001392e542e4545b8000
   56      7 0000002725ca85c8a8b700
   56      7 0000001225ca85c8a8b700
   55      7 000000244b950b91516e00
   55      7 000000114b950b91516e00
   54      7 00000022972a1722a2dc00
   54      7 00000017972a1722a2dc00
   53      7 0000002f2e542e4545b800
   53      7 0000001a2e542e4545b800
   52      7 000000345ca85c8a8b7000
   52      7 000000015ca85c8a8b7000
   47      6 0000002b950b91516e00
   47      6 0000001e950b91516e00
   46      6 0000003d2a1722a2dc00
   46      6 000000082a1722a2dc00
   44      6 00000020a85c8a8b7000
   44      6 00000015a85c8a8b7000
   43      6 0000002b50b91516e000
   43      6 0000001e50b91516e000
   42      6 0000003ca1722a2dc000
   42      6 00000009a1722a2dc000
	cBits cBytes | arg. |  chars

   40      5 0000002685c8a8b700
   40      5 0000001385c8a8b700
   39      5 000000270b91516e00
   39      5 000000120b91516e00
   38      5 000000241722a2dc00
   38      5 000000111722a2dc00
   37      5 000000222e4545b800
   37      5 000000172e4545b800
   36      5 0000002e5c8a8b7000
   36      5 0000001b5c8a8b7000
   35      5 00000036b91516e000
   35      5 00000003b91516e000
   31      4 0000003b91516e00
   31      4 0000000e91516e00
   29      4 0000003a4545b800
   29      4 0000000f4545b800
   27      4 0000003d1516e000
   27      4 000000081516e000
   25      4 00000020545b8000
   25      4 00000015545b8000
   24      3 0000002aa8b700
   24      3 0000001fa8b700
   23      3 0000003f516e00
   23      3 0000000a516e00
   21      3 0000002945b800
   21      3 0000001c45b800
   20      3 000000388b7000
   20      3 0000000d8b7000
   18      3 000000362dc000
   18      3 000000032dc000
   14      2 00000032dc00
   14      2 00000007dc00
   11      2 0000003ee000
   11      2 0000000be000
    9      2 0000002f8000
    9      2 0000001a8000
    8      1 0000003500
    8      1 0000000000
    0      0 00000000

CRC: 00

As expected, the resulting CRC is zero. The last thing to do is to write a main program to initiate the CRC computation of the shift array self-test.

namespace PolynomialDivision
{
   class Program
   {
      static void Main( string[] args )
      {
         ShiftArray shArray = new ShiftArray( 64, 0x00000035, 5 );

         shArray.SelfTest();
      }
   }// Program (class)
}// PolynomialDivision (namespace)

This program creates a shift array, passing to it a power of 2 (64 bits) to aid in the computation of the minimum number of bits to be processed, a hex representation of the generator polynomial, and the position of the most significant bit of the divisor.

Running the Code

To execute the code, unzip it to a suitable subdirectory of the Projects directory of Visual Studio 2010 (or a later version), and build it as a console application. This concludes the article on data structures for polynomial division.