Signal Segmentation Algorithm of Radhakrishnan, et al. Ported to C and C#

• Download binaries - 43.6 KB
• Download source - 140.2 KB

Introduction

Radhakrishnan, et al. proposed an algorithm for the segmentation of well logs used in the oil industry (you can find their article here). The algorithm is useful for dividing a source signal into regions where the signal can be considered constant, but with noise. The boundaries of the regions and the value of the signal within each region are not known a priori. The original algorithm was presented in FORTRAN-77. It was published, but the source code in electronic form was not available. Their algorithm has been ported to C and, in addition, a C# wrapper is provided. These ports are the focus of this article.

It should be noted that the original algorithm contained a bug that has been corrected in the current implementation. The bug allowed reading past the end of an array. The correction is noted below and in the source code. This is the only location where the current algorithm deviates from the original.

In addition to the algorithm and wrapper, unit tests are provided. The examples provided in this article are taken from the unit tests.

This article will not delve into the mathematics, as the authors of the algorithm do a rather splendid job of it. However, enough background is provided to understand the motivation and examples that follow if one has not read the original paper.

Background

Consider the figure below and suppose one wants to find the signal (the desired information), which is not known a priori, given the measurement (recorded values) which consists of the signal and some noise (unwanted random disturbance of the signal).

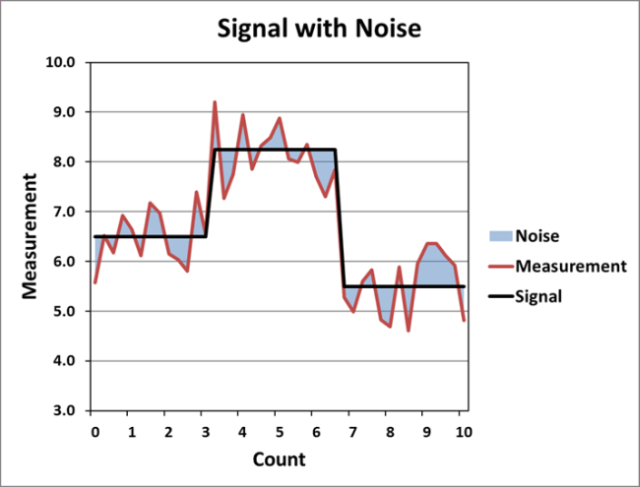
This is one type of an "inverse problem." In inverse problems, one calculates the input required to generate the given output. Inverse problems arise in a number of scientific and mathematical areas. The algorithm of Radhakrishnan, et al. is designed for a specific type of inverse problem; it segments a measured signal, whose value is allowed to vary, into regions where the signal is considered constant while allowing for noise. The authors' motivation for this is to segment logs of wells drilled in the oil and gas industry. The authors summarize their technique as:

The method is based on a univariate state variable model in which the state (signal) changes by a random amount at, and only at, the segment boundary. The observed log value is the sum of the state and random noise. The noise is modeled as Gaussian, but not necessarily stationary. The inverse problem of log segmentation is one of detecting the segment boundaries, and estimating the signal within the segment from a given log. These are solved by an iterative application of Kalman filtering and Single Most Likelihood Replacement (SMLR) techniques of Estimation theory.

Design of Libraries

The code is set up to create three usable versions of the algorithm, a C language static library, a C language DLL, and a C# language DLL. This was done to provide a range of end-use options. However, in order to keep development work to a minimum and to make maintaining the code simpler, only one version of the algorithm was implemented; the other versions were created by wrapping that version. The algorithm is written in C as C language is both efficient and widely used. This also allows the code to be used in C and C++ or wrapped to use in C# or even other environments such as Matlab (not provided). While the wrapping introduces some additional computational overhead, this was considered an acceptable trade-off to get less development work. The reasons are, firstly, the wrapping introduces only a minor overhead requirement. And secondly, when working in Matlab or C#, absolute maximum computational efficiency is typically not required. These environments are more often chosen when their ease of development outweighs the additional overhead introduced.

The Visual Studio solution contains five projects. They are listed below along with a brief summary. Note that the algorithm itself is only in the C Static Library.

• C Static Library - Contains the signal segmenting algorithm from the paper, ported from the original FORTRAN source into C
• C DLL - Creates a DLL version of the code. Links to and call the C Static Library. Does not contain code other than the DLL export function
• C Unit Tests - Unit Tests for the C Static Library
• C Sharp DLL Wrapper - Creates a C# DLL by importing the C DLL. Also provides interface classes
• C Sharp Unit Tests - Unit Tests for the C Sharp DLL Wrapper

Unit Tests

An example project was not created to demonstrate the use of the library, however, there are unit tests provided which contain examples. The unit tests make use of Visual Studio's Test Explorer/Unit Testing. An explanation of using the Test Explorer/Unit Testing is not provided here as numerous tutorials are available elsewhere. Once the solution is opened and compiled, the following unit tests should be discovered.

The unit tests are provided so that if a modification of the algorithm is needed, it can be tested. In general, the user will probably not have much need to execute the unit tests, other than to confirm the library downloaded and compiled properly. Therefore, the user will primarily be interested in LogSeparateTest and LogSeparateTestCS which demonstrates the use of the algorithm. Details about their use are provided below. These functions reproduce the example from the paper to demonstrate that the implementation is correct. In the figure below, the output provided in the paper has been plotted next to the output from the LogSeparateTestCS test.

Using the Code

Introduction

The function signatures for the C and C# versions vary from one another. The C language version duplicates the FORTRAN signature from the paper. The C# version is "modernized." This mainly entails returning the results in a single class instead of through passed parameters in the input. Overloads are also used to allow default values and to allow input in the form of lists or arrays.

One function is provided for the C version, its signature is given as:

// Input
void SegmentSignal(double LOG[], int NSAMPS, double F, 
                   int ORDER, int ORDER1, int RMODE, int NITER,
// Output
double Q[], int &NQ, double FLTLOG[], double SEGLOG[], double R[], double &C,
double &D, int &NACT, int &IER);

In total, there are six interface functions for the algorithm in C#, three for inputting the signal as a double array and three for inputting the signal as a List<double>. An example is provided below, along with the signature of the returned type, SegmentaitonResults. See SegmentSignal.cs in the C Sharp DLL Wrapper project for a complete list of calling options.

public static SegmentationResults Segment(double[] signal, double threshold,
	int jumpSequenceWindowSize, int noiseVarianceWindowSize,
	NoiseVarianceEstimateMethod noiseVarianceEstimateMethod, int maxSMLRIterations)

public class SegmentationResults
{
	...
	public double[]	BinaryEventSequence {get;}
	public int	NumberOfBinaryEvents {get;}
	public double[]	FilteredSignal {get;}
	public double[]	SegmentedLog {get;}
	public double[]	NoiseVariance {get;}
	public double	JumpSequenceVariance {get;}
	public double	SegmentDensity {get;}
	public int	Iterations {get;}
	public int	Error {get;}
	...
}

Input and Output

The algorithm has several input and output parameters. The parameters for both languages are shown in the table below, along with a brief description.

The output parameters are listed in the table below. Note that the C# parameters are returned in an instance of SegmentationResults. They are accessed as properties (for example, SegmentationResults.BinaryEventSequence).

From the output values, the most likely of interest to the user are the binary event sequence (Q/BinaryEventSequence) and the segmented log (SEGLOG/SegmentedLog). These contain the locations of the boundaries between regions and the "average" values in those regions.

Using the C Language Version

An example of using the C language version can be found under the LogSeparateTest unit test in the LogSeparateUnitTest.cpp file in the C Unit Tests library. The section of that function related to calling the algorithm can be seen below. The _data[Log] variable contains the input data which has been previously read from a file by a call to the ReadData function.

// Input values specified in paper. These do not have to be variables. They can be hard coded.
double f	= 2.50;
int order	= 10;
int order1	= 6;
int rmode	= 0;
int niter	= 300;

// Output variables. These must be variables so they can be used to return data.
double Q[_numberOfDataPoints];
int numberOfBinaryEvents;
double FLTLOG[_numberOfDataPoints];
double SEGLOG[_numberOfDataPoints];
double R[_numberOfDataPoints];
double C;
double D;
int NACT;
int error;

// Call to separate the signal.
SegmentSignal(_data[Log], 100, f, order, order1, rmode, niter,
	            Q, numberOfBinaryEvents, FLTLOG, SEGLOG, R, C, D, NACT, error);

Using the C# Language Version

An example of using the C# language version can be found under the LogSeparateTestCS unit test in the LogSeparateUnitTest.cs file in the C Sharp Unit Tests library. The section of that function related to calling the algorithm can be seen below. The _data[(int)InputType.Log] variable contains the input data which has been previously read from a file by a call to the ReadData function.

Please note that when using the C# version, it is necessary to have the C language DLL in the same directory. That is, it requires both SegmentSignalCS.dll and SegmentSignal.dll. This requirement results from the C# version wrapping and calling the C version.

// Input values specified in paper.
private const double            _f          = 2.50;
private const int               _order      = 10;
private const int               _order1     = 6;
private const int               _niter      = 300;
NoiseVarianceEstimateMethod     _rmode      = NoiseVarianceEstimateMethod.Point;

...

// Call to separate the signal.
SegmentationResults results = SegmentSignal.Segment(_data[(int)InputType.Log], _f, _order,
                                                    _order1, _rmode, _niter);

Modification of Algorithm

During the use and testing of the algorithm, it was discovered that, with certain input, it was possible to access memory past the end of an array. The offending function is called GETSPK in the original paper. The new function, GetSpikeyZone, in the current implementation is below:

// Original function name: GETSPK
void GetSpikeyZone(double Q[], int NSAMPS, int SEGSTR, int &SEGEND, bool &endofarray)
{
	// Function:
	// Identifies a zone of spikes.  A spiky zone is defined by 0,1,1,...,1,0.
	//
	// Input parameters:
	// Q: Binary event sequence in which the zone is to be identified.
	//
	// NSAMPS: Length of the array Q.
	//
	// SEGSTR: Sample number where the spiky zone starts.
	//
	// Output parameters:
	// SEGEND: Sample number where the zone ends.
	//
	// endofarray: End of data indicator.
	//		true: End of array reached.
	//		false: Not at end of the array.

	SEGEND = SEGSTR;
	if (Q[SEGEND] < 0.5)
	{
		// Modified from original paper. 
        // The "if" statement below was not part of the original
		// algorithm.
		//
		// It seems there can be a case where Q[i] < 0.5 for SEGEND = NSAMPS 
        // that causes us to miss
		// flagging the end of the array. 
        // Do a check here to ensure we don't overrun the end of
		// the array and over write memory we should not over write.
		if (SEGEND >= NSAMPS)
		{
			endofarray	= true;
			SEGEND		= NSAMPS - 1;
		}

		return;
	}

	do
	{
		SEGEND++;
	}
	while ((Q[SEGEND] > 0.5) && (SEGEND < NSAMPS));

	if (SEGEND >= NSAMPS)
	{
		endofarray = true;
	}

	SEGEND--;
}

Where the following was added to prevent returning with an array indexer larger than the size of the array.

if (SEGEND >= NSAMPS)
{
	endofarray	= true;
	SEGEND		= NSAMPS - 1;
}

Concluding Remarks

This article merely provides a port of the algorithm from FORTRAN to C and C# while making the binaries and the source code available for immediate use. The only contribution made to the original algorithm is to correct a bug that allowed reading past the end of an array under certain conditions.

While the original motivation for the algorithm was for segmenting well logs, this algorithm has applications elsewhere. The author of this article has used it to segment both well logs and data generated from various laboratory experiments. It can be used as part of a process used to automate the analysis of signals; separate regions can be detected and processed without requiring a user to identify regions of interest.

Acknowledgment

Thanks to APS Technology for allowing this article to be published.

History

• June 2015 - First release
• October 2019 - Grammar and spelling corrections