Algorithms for Calculating Convergent Series

• Download convergent_series.zip - 798 B

Introduction

When computer science students learn the concepts of control structures, particularly repetition structures, they often come across exercises involving converging series.
Thinking about this difficulty, I have separated classical algorithms involving some of these series.

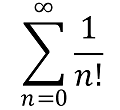
Background

A series is convergent if the sequence of its partial sums tends to a limit (L). That means that the partial sums become closer and closer to a given number when the number of their terms increases. If the series is convergent, the number L (necessarily unique) is called the sum of the series. (WikiPedia)

Let's look at some examples of convergent series:

1. The Euler constant obtained by the Taylor series (reciprocals of factorials)

   ℇ = 1/1 + 1/1 + 1/2 + 1/6 + 1/24 + 1/120 + ...

2. The PI Number obtained by the Leibniz series

   π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/10 + ...

3. Reciprocal Fibonacci constant

   ψ = 1/1 + 1/1 + 1/2 + 1/3 + 1/5 + 1/8 ...

4. Sum of Geometric progression

   1 = 0,9 + 0,09 + 0,009 + 0,0009 + 0,00009 + ...

Using the Code

The algorithm below was developed with the Python language using the Thony IDE.

# Calculating some convergent series
# 
# Language: Python

# 2018, Jose Cintra
# josecintra@josecintra.com

import math

# 1.0 Calculating Euler's constant by the Taylor series (More readable version)

v = 0.0 # convergence value
i = 0 # control variable for the loop
n = 100 # iterations number for the loop
for i in range(0,n):
    v = v + 1 / math.factorial(i)

print('e = ',v)
print()

# 1.1 Calculating Euler's constant by the Taylor series (Faster version)

v = 1.0 # convergence value
i = 0 # control variable for the loop
n = 100 # iterations number for the loop
fat = 1 # factorial
for i in range(1,n):
    fat = fat * i
    v = v + 1 / fat
    
print('e = ',v)
print()


# 2.0 Calculating PI/4 by the Leibniz series 

n = 1000000 # iterations number for the loop
v = 0.0 # convergence value
i = 0 # control variable for the loop
sign = 1 # Controls signal switching in series
for i in range(1,n,2):
  v = v + sign * (1 / i)
  sign = -sign

print('pi/4  = ',v)
print('pi  = ', v * 4)
print()

# 3.0 Reciprocal Fibonacci constant (Using the Binet Fórmula)
n = 1000 # iterations number for the loop
v = 0.0 # convergence value
i = 0 # control variable for the loop
fib = 1.0 # Calculate fibonacci number by the index
for i in range(1,n):
  fib = round((pow((1+math.sqrt(5))/2,i)-pow((1-math.sqrt(5))/2,i))/ math.sqrt(5))
  v = v + (1 / fib)
  
print('fi  = ',v)
print()

# 3.1 Reciprocal Fibonacci constant (Faster version)
n = 1000 # iterations number for the loop
i = 0 # control variable for the loop
v = 0.0 # convergence value
fib = 0.0 # Fibonacci number
last = 1.0 # auxiliar var for fibonacci calculation
for i in range(1,n):
  fib,last = last,fib + last
  v = v + (1 / fib)
  
print('fi  = ',v)
print()

# 4.0 Sum of Geometric progression 
n = 999999999999 # iterations number for the loop
v = 0.0 # convergence value
i = 10 # control variable for the loop

while (i < n):
  v = v + (9 / i)
  i = i * 10
  
print('gp  = ',v)
print()

# end

//

Points of Interest

1. The value of the variable n is free so that the student can do experiments. In fact, it is possible to optimize the algorithms using appropriate values of this variable;
    
2. The algorithms 1 and 3 were developed in 2 versions: a more readable and, therefore, more maintainable and a faster version.
   To calculate the Fibonacci numbers individually in the algorithm 3.0, we use the Binet formula.
    
3. There are some controversies about the performance of the while and for range control structures in Python. Since version 3.0 the range structure has been improved and may be a good choice.
    
4. To calculate the Euler constant, we use the factorials . The factorial value tends to grow very quickly, so care must be taken to avoid overflow errors.

Last Words

Thanks for reading!

I also made a version of these algorithms using the Haskell functional language. Look here: https://www.codeproject.com/Tips/1265626/Working-with-numerical-lists-in-functional-languag

For more algorithms, visit github.