Introduction
When computer science students learn the concepts of control structures, particularly repetition structures, they often come across exercises involving converging series.
Thinking about this difficulty, I have separated classical algorithms involving some of these series.
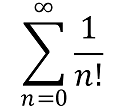
Background
A series is convergent if the sequence of its partial sums tends to a limit (L). That means that the partial sums become closer and closer to a given number when the number of their terms increases. If the series is convergent, the number L (necessarily unique) is called the sum of the series. (WikiPedia)
Let's look at some examples of convergent series:
- The Euler constant obtained by the Taylor series (reciprocals of factorials)
ℇ = 1/1 + 1/1 + 1/2 + 1/6 + 1/24 + 1/120 + ...
- The PI Number obtained by the Leibniz series
π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/10 + ...
- Reciprocal Fibonacci constant
ψ = 1/1 + 1/1 + 1/2 + 1/3 + 1/5 + 1/8 ...
- Sum of Geometric progression
1 = 0,9 + 0,09 + 0,009 + 0,0009 + 0,00009 + ...
Using the Code
The algorithm below was developed with the Python language using the Thony IDE.
import math
v = 0.0
i = 0
n = 100
for i in range(0,n):
v = v + 1 / math.factorial(i)
print('e = ',v)
print()
v = 1.0
i = 0
n = 100
fat = 1
for i in range(1,n):
fat = fat * i
v = v + 1 / fat
print('e = ',v)
print()
n = 1000000
v = 0.0
i = 0
sign = 1
for i in range(1,n,2):
v = v + sign * (1 / i)
sign = -sign
print('pi/4 = ',v)
print('pi = ', v * 4)
print()
n = 1000
v = 0.0
i = 0
fib = 1.0
for i in range(1,n):
fib = round((pow((1+math.sqrt(5))/2,i)-pow((1-math.sqrt(5))/2,i))/ math.sqrt(5))
v = v + (1 / fib)
print('fi = ',v)
print()
n = 1000
i = 0
v = 0.0
fib = 0.0
last = 1.0
for i in range(1,n):
fib,last = last,fib + last
v = v + (1 / fib)
print('fi = ',v)
print()
n = 999999999999
v = 0.0
i = 10
while (i < n):
v = v + (9 / i)
i = i * 10
print('gp = ',v)
print()
//
Points of Interest
- The value of the variable
n is free so that the student can do experiments. In fact, it is possible to optimize the algorithms using appropriate values of this variable;
- The algorithms 1 and 3 were developed in 2 versions: a more readable and, therefore, more maintainable and a faster version.
To calculate the Fibonacci numbers individually in the algorithm 3.0, we use the Binet formula.
- There are some controversies about the performance of the
while and for range control structures in Python. Since version 3.0 the range structure has been improved and may be a good choice.
- To calculate the Euler constant, we use the
factorials . The factorial value tends to grow very quickly, so care must be taken to avoid overflow errors.
Last Words
Thanks for reading!
I also made a version of these algorithms using the Haskell functional language. Look here: https://www.codeproject.com/Tips/1265626/Working-with-numerical-lists-in-functional-languag
For more algorithms, visit github.
