Sometimes seeing is believing. A working solution helps examine this octree's operation and accuracy.
Introduction
This tip/trick examines the operation of code from another tip/trick first posted on 4th November, 2015. Sometimes, reading a tip/trick's text raises questions you don't see answered by just reading the code. What does "neighboring space" mean? Does "precision distance check" mean Euclidean distance? The Introduction and Background sections there sound about right but does this implementation really find nearest-neighbor colors? It's useful to have a full, running solution (or two) to see results that help in answering these questions and to allow better understanding of operation.
One question I will answer here is, "Why use a palette entry with the smallest distance to an image pixel in the first place?" The answer is quantization. We are trying to use fewer colors to make an image more compressible. Colors used from a palette means there will only be pixels with these same quantized colors. Repeated colors can be represented with less memory/file size/stream length using various compression methods (DCT in JEPG, fewer/smaller frequency components) saving time and/or memory space.
If you want to understand more about this general area, you can visit Binary search tree (BST). "See also" there has references to other search tree types. You can imagine two BST's combined into a Quadtee (two times binary equals quad) to search for points having two disjoint or orthogonal value ranges. Then, think of OctTrees or octrees that allow quick neighbor searches in a set of three dimensional points (binary cubed is oct). These 3D points are our color palette.
About the Code
Where the dynamichel Tip/Trick has:
public Color[] GetNearestColors(Color[] sourceColors, Color[] imageColors) {
Color[] ret = new Color[imageColors.Length];
ColorFinder clfTmp = new ColorFinder(sourceColors);
for(int i = 0; i < imageColors.Length; i++) {
int iNearestColorIndex_i = clfTmp.GetNearestColorIndex(imageColors[i]);
ret[i] = sourceColors[iNearestColorIndex_i];
}
return ret;
}
The downloadable ckDynamichaelColors solution's MainWindow.xaml.cs has:
private Color[] GetNearestColors(Color[] sourceColors, Color[] imageColors) {
Color[] ret = new Color[imageColors.Length];
ColorFinder clfTmp = new ColorFinder(sourceColors);
for(int i = 0; i < imageColors.Length; i++) {
int iNearestColorIndex_i = clfTmp.GetNearestColorIndex(imageColors[i]);
ret[i] = sourceColors[iNearestColorIndex_i];
}
return ret;
}
ColorFinder is emphasized in the code snippets. The ColorFinder class is the interface for building and searching dynamichel's octree. It has one constructor and one instance method:
public ColorFinder(Color[] sourceColors) {
_nodRoot = new Node(0, sourceColors);
for(int i = 0; i < sourceColors.Length; i++) {
_nodRoot.AddColor(i);
}
}
public int GetNearestColorIndex(Color color) {
int iTmp;
return _nodRoot.GetNearestColorIndex(color, out iTmp);
}
There were a few points that took me a while to get. Node is an inner or nested class of ColorFinder. ColorFinder makes the first root Node (_nodRoot), but all other Nodes are created during the ColorFinder's calls on _nodRoot.AddColor(i). Good for data protection but bad for accessing octree data by a demo application.
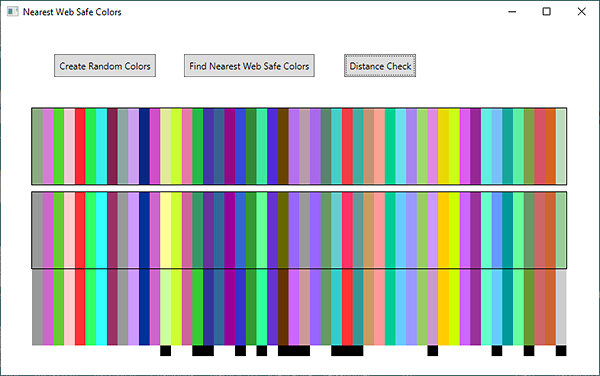
Please try building and running the ckDynamichaelColors solution. Click on the Create Random Colors button to display a banner of 50 random 'image' colors:

Next, click on the Find Nearest Web Safe Colors button to search the source colors in the octree created by our ColorFinder and to display those that are nearest to the top banner of random colors. There are 216 source colors which is 6 cubed.

Notice there are slight color differences between the top and middle banners since the 216 source colors are outnumbered by 16 million possible random colors. Now click the Check Distance button. A third banner is displayed. It shows nearest source color by exhaustive search of the source colors for each random image color. This is shown at the start of this tip. There are small black squares displayed below the third set of colors wherever the octree-found nearest color in the middle banner and the exhaustive-search nearest color in the bottom banner differ. If you are running this is in a Visual Studio debug session, you will see more information about the differences in the Output pane.
Note the top of the MainWindow.xaml.cs file:
using System
using System.Collections.Generic;
using System.Diagnostics;
using System.Threading.Tasks;
using System.Threading.Tasks;
using System.Windows;
using System.Windows.Controls;
using System.Windows.Media;
namespace ckDynamichaelColors
{
You can uncomment and use the RESTRICT_SRC defined on line 1 to restrict channel color differences to 3 bits (vs. 8 bits unrestricted). There are still 216 source colors. They just cover a smaller gamut than the Web Safe colors. Rebuild the solution and repeat the three steps above. You will get results like this:

Most octree-found nearest colors and exhaustive-search nearest colors differ. Let's take one last extreme example. We have only two source colors. They are 0xFF7F7F7F and 0xFFFCFCFC. (The leading 0xFF byte is the alpha channel that means completely opaque, not even a little bit transparent). We want to find the nearest source color to the single image color 0xFF808080. Build and run the ckTwoSourceColors solution. You should see this output:

We could have chosen white, 0xFFFFFFFF, for the second source color instead if 0xFFFCFCFC, but the octree-found nearest color would be invisible against the background of the second banner.
What's the Diff?
To be fair, dynamichael said fast but only "as precise as possible without being slow". Yes, you wouldn't want to quantize or reduce colors in a stream of multi-megapixel image frames using exhaustive nearest neighbor searching for each pixel, but why exactly is there any imprecision in building or using the dynamichael octree?
I first suspected the distance function had something to do with the differences. The Node class has a static Node that initializes a single private static int[,] Distance in the Node class.
private static int[,] Distance = new int[256, 256];
...
static Node() {
for(int i = 0; i < 256; i++) {
for(int ii = 0; ii < 256; ii++) {
Distance[i, ii] = ((i - ii) * (i - ii));
}
}
}
This Distance array is used when searching the octree in Node's GetNearestColorIndex method. Each Node in an octree has as many as eight child Nodes but as few as one Node at levels 0 through 6 in this implementation. This is the code that finds the child having a source color nearest the given image color (color and '<' are emphasized in the code snippet).
int iMinDistance = int.MaxValue;
int iMinColor = -1;
foreach(Node nod in _anodChildren) {
if(nod != null) {
int iDistance_nod;
int iColor_nod =
nod.GetNearestColorIndex(color, out iDistance_nod);
if(iDistance_nod < iMinDistance) {
iMinDistance = iDistance_nod;
iMinColor = iColor_nod;
}
}
}
ret = iMinColor;
distance = iMinDistance;
It's a simple foreach loop that finds the child with the source color having the smallest distance to the image color and returns that source color's index. Remember we added all the source colors to the octree when we instantiated our ColorFinder. Also note that:
nod.GetNearestColorIndex(color, out iDistance_nod);
is a recursive call in this method. In this way, we search the octree level by level calling GetNearestColorIndex until we are finally at level 7:
if(_iLevel == 7) {
ret = _iColorIndex;
distance = ( Distance[color.R, _aclSourceColors[ret].R] +
Distance[color.G, _aclSourceColors[ret].G] +
Distance[color.B, _aclSourceColors[ret].B] );
}
We will look at this distance assignment shortly but it is important to recognize one thing that took me awhile to appreciate: different children have different distances to the image color. That means we must be reaching level 7 for each child searched. That means 8 levels of nodes with a maximum of 8 children each are searched to find the nearest color for the ColorFinder caller. That's 8 x 8 or 256 searches. I still don't know where minus 1 comes in, but I believe this is what dynamichael is saying where the tip reads "we will only have to perform up to 255 comparisons instead of potential thousands."
BTW, what would happen if we use a source palette with much less or more than 216 colors? It would be easy to do since we have over 16 million 24-bit colors to choose from. We can try one set with 3³ or 27 source colors, and another with 9³ or 729 source colors. We should spread the source colors out like those in Safe Web colors. That would mean picking color channel components from 0, 127, and 255 for the 27-color source set and from 0, 32, 64, 96, 127, 159, 191, 223, and 255 for the 729-source colors set. You can make these changes in the // Web Safe colors. part of MainWindow.xaml.cs:
public MainWindow()
{
InitializeComponent();
#if RESTRICT_SRC
pick.Add(0x80);
pick.Add(0x90);
pick.Add(0xA0);
pick.Add(0xB0);
pick.Add(0xC0);
pick.Add(0xD0);
#else // Web Safe colors. Max diff between values, 8 bits change.
pick.Add(0);
pick.Add(51);
pick.Add(102);
pick.Add(153);
pick.Add(204);
pick.Add(255);
#endif
In a version of dynamichael's octree code that reports node information, I got these results:

Notice the 216 Web Safe source colors are at or near a sweet spot in having the fewest exhaustive-search differences. Notice something else: at level 2 for the small set, level 3 for the Web Safe set, and level 4 for the big set, the number of nodes at those levels reach the number of source colors. From there to higher-numbered levels, each node must have only one child. Meaning we really only need to search to these levels (2, 3, and 4) for the same result as searching all 8 levels. I changed the relevant sections of the Node class (note emphasized level 3) and got the same average number of mismatches for the Web Safe set.
public void AddColor(int colorIndex) {
if(_iLevel == 3) {
...
public int GetNearestColorIndex(Color color, out int distance) {
int ret = -1;
if(_iLevel == 3) {
We could save search time by having a two phase octree builder in ColorFinder. The first phase would build the whole 8 level tree. Remember we had to reach level 7 to know nearest colors for each child searched. Then, the second phase would rebuild the octree for ColorFinder-caller searches but would limit the octree to the lowest-numbered effective level.
Now, about this distance thing. For Euclidean space, shouldn't distance be √(R² + G² + B²)? And why aren't Distance values in float or double instead of int?
I was finally able to convince myself that square roots weren't needed for comparison. We only need to compare two different values, square rooted or not, to decide 'nearer'. We don't need the distance itself. Notice
public int GetNearestColorIndex(Color color)
in the ColorFinder class 'protects' the application from seeing distance. It's up to us app coders to fix that flaw if needed. But the type seemed to me to be a real problem. Maybe we do need to coerce distance calculations to double AND take the square root. Alas, this is probably not so. In comparing the number of differences in 25000 nearest color searches, 34.6% of the search colors were different between octree and exhaustive search methods when double was used. This compares to 34.8% mismatches using squared ints. I did not measure the time it took for these 25000 searches but likely using ints and not using square root was faster.
Where's the Beef?
The extreme example suggests the real culprit in mismatches. I think a simple diagram will help. We can use smaller color values to see the same problem. Let's use the two 4-bit source colors 0x777 and 0xFFF. The single image color is 0x888. (No alpha channel this time. Just 4-bit rgb.) For this particular example, since each color has all three channel components with the same value, let's try reducing the 3-dimensional octree to a single dimensional binary search tree. (Oh, so we are back to BSTs?) - not quite. This time, when we diagram the tree, as we move vertically down from one level to the next, we make the horizontal position proportional to the most significant N bits of each color. By the time we map down to the leaf level, we will see the relative location of all three colors.

It's easy to see that first step is a doozy. Because the first bit of the image color is 1, we search all the children of source color F. It puts us where we can't find the correct nearest source color. Now imagine this is a subtree somewhere in an 8-bit BST. Finally, imagine subtrees like this that are othogonal to each other in an 8-bit octree. Instead of moving down level by level, we use level as a fourth dimension. Instead of descending, we just move to another lower level octree somewhere else. These doozies don't have to be at the same Node, and they don't seem to be all that common since only 1/3 of the searches lead to a nearest color difference, but I think collectively they account for the mismatches we see. Most often the mismatches are one-off source color wise, and 2/3 of the time they are correct. For the speed, maybe the imprecision is a small cost.
Now for the homework. What modification can reduce this octree's search errors without costing too much of a speed reduction?
History
- 3rd July, 2021: Initial version
