This sort uses statistical analysis to find an ideal pivots. When an ideal pivot is found, the list is separated into two and half is given to a newly created thread. By keeping track of how many worker threads will be created, we reduce overhead and can get a fully sorted list quickly.
Introduction
This is an example of a sort that is multi threaded. Sorting can cause delays for the user. Most sorts are single threaded, but most computers have multiple cores that could help with the sort and remove the slowdown. This sort is intended to provide an example of how a sort can be multi-threaded and also faster than the original it is based on.
Using the Code
This code is primarily set up for timing and takes a vector or ints.
std::vector<int> arr;
for(int i = 0; i < 10000; i++)
{
arr.push_back(temp);
}
std::random_shuffle( arr.begin(), arr.end());
splitQuick(arr);
Points of Interest
The statical part of this algorithm, the place were we pick the ideal pivot is very short.
We simply create a list of Candidates, we then sort the list and then select the one that is in the center to best approximate what we think the complete list will be.
std::vector<int> arr;
for(int i = 0; i < 10000; i++)
{
arr.push_back(temp);
}
int selection = 513;
std::vector<int> candidates;
for(int j = 0; j < selection, j++)
{
candidates.push_back( arr[ rand() % array.size() );
}
std::sort (candidates.begin(), candidates.end());
int pivot = candidates[candidates.size()/2];
This algorithm lets the worker threads recruit additional threads. It allows the work to be properly divided quickly. The "magnitude" variable tells the thread how many more times it can split.
total(int magnitude)
{
while (magnitude > 0)
{
name = name << 1;
int tempName = name | 1;
magnitude--;
total(magnitude, tempName);
}
]
std::cout << name << std::endl;
}
void splitQuick()
{
total(3, 0);
}
int main()
{
splitQuick();
}
Result
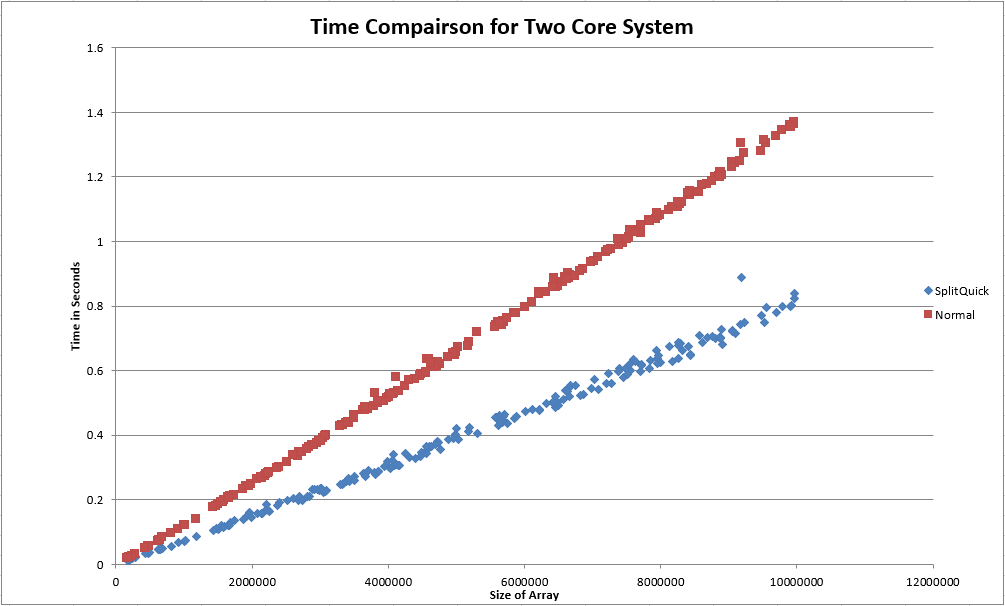
This sort does have extra overhead and does consume extra processing power, but gets the results faster by using the additional resources available.
History
- 24th May, 2022: First draft complete
