You may have data that is conceptually set in an upper triangular matrix, but is actually stored in a 1d array. There comes a moment when you need to get the row/column indices of the entries. This tip has the formulas to derive them.
Introduction
"a square matrix is called upper triangular if all the entries below the main diagonal are zero" (Wikipedia), thus the main diagonal is included.
It is surely a shortcoming of mine, possibly laziness, but browsing a bit for the formulas for transforming 1D linear indices into 2D upper triangular ones, and vice versa, I found many pages proposing formulas that do not take the main diagonal into account (f.e., this one), but very few accounting for it. Well, one could just use a fake number of rows/columns, but that is not elegant, is it? So I thought it was better to derive the formulas myself, not a great deed in itself, and put them in this tip. Maybe someone else will find them useful, or maybe there is an error that I did not see and someone will point it out.
The idea is to have, for example, an array with 15 cells (e.g., [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14]) that conceptually correspond to the cells of the 2D upper triangular matrix shown in the following figure. All blank cells below the main diagonal are 0s. For example, I need to derive that the cell with index 10 in the array has indices 2,3 in the matrix.
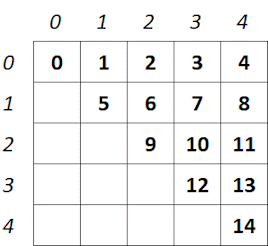
The Derivation
Step by Step Walk-Through
Assume the 2D matrix has \(n\) rows (and \(n\) columns), therefore \(n^2\) cells, which are all 0s below the main diagonal. The first task is to identify the first 1D index, \(k\), of each row \(i, 0\leq i \lt n\). Notice that this is simply obtained by subtracting from the total number of the cells up to row \(i\) the number of cell below the main diagonal up to that row. This means that the desired index \(k\) can be obtained as:
$k = i\cdot n - \frac{i(i-1)}{2}$
or, equivalently (please, forgive my pedantry):
$2k = 2i\cdot n - i^2 + i$
thus:
$i^2 - (2n+1)i +2k = 0$
which is solved as:
$i = \frac{2n+1 \pm \sqrt{ (2n+1)^2 - 8k}}{2}$
yielding:
$i = \frac{1}{2}\left( 2n+1 \pm \sqrt{4n^2 + 4n -8k +1} \right)$
where only the positive component needs to be considered.
Having index \(i\), index \(j\) is then easily obtained by subtracting from \(k\) all elements up to the first of the corresponding row:
$j = k - \left( i\cdot n - \frac{i(i-1)}{2} \right)$
which also permits to get \(k\) having \(i\) and \(j\).
Implemented Code
There is really no need to present two lines of code, but here goes. The demo project asks for n and writes the upper triangular matrix where the cells have been placed by the two lines:
i = (int) (0.5*(2*n+1-Math.Sqrt(4*n*n + 4*n - 8*k + 1)));
j = (int) (k - (i*n - 0.5*i*i - 0.5*i));
This is C#, but of course, just by changing a couple of parentheses here and there, you get the equivalent in Python, C++, ...
Bonus Detail
One last detail. You might have a linear array and wonder what is the number of rows/columns of the 2D matrix that the array holds the upper triangular matrix of. Well, if the number of cells of the array is \(m\), than this number must satisfy the equation:
$m = \frac{n(n+1)}{2}$
thus \(2m = n^2 + n\) or \(n^2 + n - 2m =0\), therefore:
$n = \frac{-1 \pm \sqrt{1+8m}}{2}$
You don't get a positive integer? You did not have a correct number of cells to start with.
Conclusion and Points of Interest
This tip presents a simple derivation of the formulas needed to compute the indices of the cells of a linear array when it is reshaped into an upper triangular matrix, i.e., a 2D square matrix in which all cells below the main diagonal are zeros. This option is more versatile than expected, for example, it provides an efficient way to store a symmetric matrix in memory.
History
- 20th September, 2023: Initial version
