Introduction
This source code is for understanding the Levenshtein Edit Distance algorithm easily. When I began to search this algorithm, I was so scared to implement it. I read all of
the articles about
this algorithm and I really didn't understand anything. When my research was deepening, I was
trying to figure out the secret of this common algorithm. When I finished implementing it,
I decided to write an article on CodeProject.com. I am hoping my implementation would be useful for people who work to understand
The Levenshtein Edit Distance algorithm.
Background
This algorithm is so commonly used for Microsoft Outlook or Microsoft Word Spell Checking systems and Google.
So thanks Vladimir Levenshtein for this algorithm. I will not
try to explain the algorithm's details to you. The purpose of this article is for you to follow steps
and see the flow chart of algorithm easily.
About the Algorithm
The edit distance between two strings is defined as the minimum number of edit operations required to transform one string into another. Let’s assume that the first string is named
as the target string and the second string is named as the source string. We want to convert
the source string to target. An edit is one of three operations: a delete (a character from the source string),
an insert (a character from the target string), and a substitute (a character from the source string with a character from the target string). There is a fourth operation, named as match,
which does not count as an edit. Consider two input strings "activate" and "caveat". Below you can see one possible transformation. In the example, a transformation
is represented by a string consisting of the characters M for match, S for substitute, D for delete, and I for insert.
D M D S M I M M D
a c t i v a t e
c a v e a t
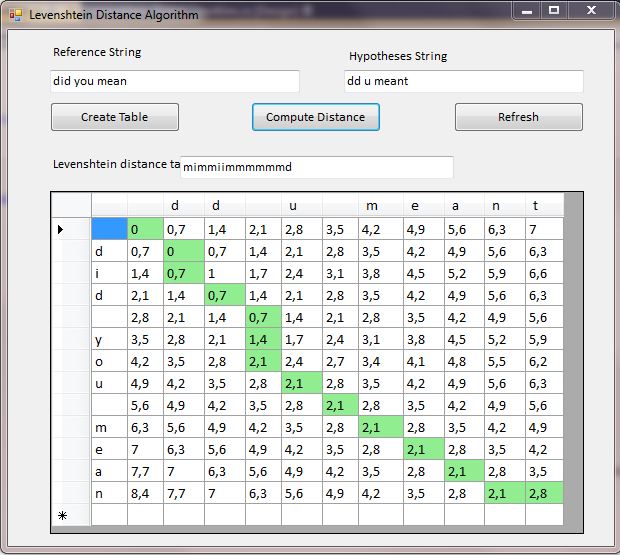
Figure 1: Levenshtein Edit Distance algorithm GUI
Using the code
I will share some code snippets of my implementation here:
In our implementation:
- Delete cost = 0.7
- Insert cost = 0.7
- Substitute cost = 1.0
Match does not have a cost.
Reference = Ref_text_box.Text;
Hypotheses = Hyp_text_box.Text;
distance_table = new double[Reference.Length + 1, Hypotheses.Length + 1];
for (int i = 0; i <= Reference.Length; i++)
distance_table[i, 0] = i * 0.7;
for (int j = 0; j <= Hypotheses.Length; j++)
distance_table[0, j] = j * 0.7;
for (int i = 1; i <= Reference.Length; i++)
{
for (int j = 1; j <= Hypotheses.Length; j++)
{
if (Reference[i - 1] == Hypotheses[j - 1]) distance_table[i, j] = distance_table[i - 1, j - 1];
else {
distance_table[i, j] = Math.Min(Math.Min(distance_table[i - 1, j - 1] + 1,
distance_table[i - 1, j] + 0.7), distance_table[i, j - 1] + 0.7);
}
}
}
String distance_string = " ";
String distance_result;
int i = Reference.Length, j = Hypotheses.Length;
while (true)
{
this.dataGridView1.Rows[i].Cells[j+1].Style.BackColor = Color.LightGreen;
if (i == 0 && j == 0)
{
this.dataGridView1.Rows[i].Cells[j].Style.BackColor = Color.LightGreen;
distance_string_textbox.Text = distance_string;
char[] a = distance_string.ToCharArray();
Array.Reverse(a);
distance_result = new string(a);
distance_string_textbox.Text = distance_result;
break;
}
else if (i == 0 && j > 0)
{
this.dataGridView1.Rows[i].Cells[j+1].Style.BackColor = Color.LightGreen;
distance_string += "d"; j--;
}
else if (i > 0 && j == 0)
{
this.dataGridView1.Rows[i].Cells[j+1].Style.BackColor = Color.LightGreen;
distance_string += "i"; i--;
}
else
{
if (distance_table[i - 1, j - 1] <= distance_table[i - 1, j] &&
distance_table[i - 1, j - 1] <= distance_table[i, j - 1])
{
this.dataGridView1.Rows[i].Cells[j+1].Style.BackColor = Color.LightGreen;
if (distance_table[i - 1, j - 1] == distance_table[i, j])
distance_string += "m"; else
distance_string += "s";
i--;
j--;
}
else if (distance_table[i - 1, j] < distance_table[i, j - 1])
{
this.dataGridView1.Rows[i ].Cells[j+1].Style.BackColor = Color.LightGreen;
distance_string += "i"; i--;
}
else if (distance_table[i, j - 1] < distance_table[i - 1, j])
{
this.dataGridView1.Rows[i].Cells[j +1].Style.BackColor = Color.LightGreen;
distance_string += "d"; j--;
}
}
}
Points of Interest
This code snippet will teach to understand the Levenshtein Edit Distance algorithm easily. You can try some words and sentences to compare each other and you can follow
the distance table
to understand how to compute the distance of your strings.
