This article is based on Chapter 2 of my unpublished textbook "Applied Algorithms and Data Structures." All the code presented here, and included in the downloadable ZIP file, was written in unmanaged C++ under Visual Studio 2010. (The code was adapted from the original code developed under Borland C++ a long time ago, as indicated in each of the files.)
Generic Singly-Linked Lists
The use of dynamic memory in conjunction with structures to store data and pointers to structures allows maintaining lists whose length is only limited by the amount of heap space. In order to implement lists for different data types we can define generic singly-linked lists (GSLLs) as shown in the following figure.
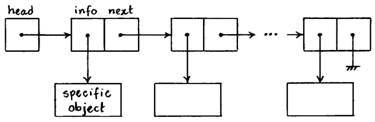
In a GSLL, the info field is a generic pointer that points to an object of some type, while the next field works as usual. The object pointed to by the info field is created in the code that uses a specific derived implementation of the GSLL. The following declarations are suitable to manipulate GSLLs.
typedef void * genPtr;
typedef struct gSLLstruct gSLLstr;
typedef gSLLstr * gSLLptr;
struct gSLLstruct {
genPtr info;
gSLLptr next;
};
The advantage of using GSLLs is that the algorithms to manipulate lists are implemented once and for all. Then, for each specific data type, individual functions are defined (outside of the list-manipulation functions) to handle the printing, comparison, allocation and deletion of list objects pointed to by the info fields. In this way, it is possible to support polymorphic SLLs co-existing at the same time in a single program.
Generic Doubly-Linked Lists
Generic doubly-linked lists (GDLLs) are an improvement upon GSLLs in that they allow deletions of elements in constant time. The following definitions would be suitable for implementing GDLLs:
typedef struct gDLLstruct gDLLstr;
typedef gDLLstr * gDLLptr;
struct gDLLstruct {
genPtr info;
gDLLptr pred, succ;
};
Consider now the situation in which we are given a pointer p to an element in a list with the request to delete it. If the element were in a singly-linked list, we would have to traverse the list from the head until we found a node at q such that q->next == p. Upon finding such a node, the removal of the element at p would be accomplished by the code:
q->next = p->next;
free( p->info );
free( p );
(Of course, the special case in which the element at p is the very first element pointed to by head must also be considered.)
If the element to be deleted belongs to a doubly-linked list, then by careful implementation of the list it is possible to avoid searching for the element preceding it. In the general case, if the element is somewhere in the middle of the list, a graphical representation of the logical relationship of the element and its predecessor and successor elements might be as follows:

Then the removal and deletion of the element at p is easily achieved by the following code:
p->pred->succ = p->succ;
p->succ->pred = p->pred;
free( p->info );
free( p );
In the implementation of GDLLs, it is necessary to decide what to do with the first and last elements. In particular, what to assign to the pred field of the first element and to the succ field of the last element. If we assign NULL to both fields, thus terminating the list at both ends, as shown below,

we face the problem of implementing three different cases for ordered insertions and arbitrary deletions, namely the first element, somewhere in the middle of the list, and the last element. Clearly, there must be a better way to do things.
If the GDLL is made circular, so that the predecessor of the first element is the last one and the successor of the last element is the first one, then the same code can be used to implement ordered insertions and arbitrary deletions. The only requirement is that, when conducting searches on the list, we have a means of knowing when we have returned to the beginning. This is easily accomplished by maintaining a head pointer to a dummy first element, as shown below with a NULL (crosshatched) info field. Insertions and deletions are always started at the successor of the dummy element.

An initially empty GDLL consists of the single dummy element with its pred and succ fields pointing to the element itself:

Generic, Doubly-Linked, XOR-Coded Lists
The disadvantage of implementing GDLLs with explicit pred and succ pointers is the waste of space due to the duplication of pointers. For any two logically-adjacent elements at p and q, with the element at q being after the one at p, the assertion q == p->succ && p == q->pred is true. In addition, for any node at q in a circular GDLL q->pred->succ == q->succ->pred == q also holds. These assertions simply state that the address of each element is stored twice in the list.
The solution to the waste of space is to encode in a single field of each element a suitable composition of the addresses of its predecessor and successor elements. This encoding is implemented by applying the exclusive-or (xor, ^) function to addresses (see Thomas A. Standish, Data Structure Techniques, Addison-Wesley 1980, pp. 196-198; Harry R. Lewis and Larry Denenberg, Data Structures and Their Algorithms, Harper Collins 1991, pp. 88-90. Standish, pp. 82-83, also describes the use of this technique in the Siklossy traversal of binary trees: L. Siklossy 1972, "Fast and Read-Only Algorithms for Traversing Trees Without an Auxiliary Stack," Inf. Proc. Letters 1, 149-152.)
The xor function over two logical variables A and B, is defined as xor( A, B ) == 0 if A == B, and xor( A, B ) == 1 if A != B. Furthermore, using the xor operator (^), this function has the following properties
commutativity: A ^ B == B ^ A
associativity: A ^ (B ^ C) == (A ^ B) ^ C
self-cancellation: A ^ A == 0 [in particular A ^ (A ^ B) == B]
when applied as addition, it generates no carry.
As a simple illustration of the usefulness of the self-cancellation property of the xor function, we can write a macro to swap any two variables of the same primitive data type without using a temporary variable, as follows:
#define swap( x, y ) ( x ^= y, y ^= x, x ^= y )
To see how this works, consider the execution of the following code
int i = 12, j = 7;
swap( i, j )
Representing the integers as four-bit binary numbers, the results of the sequential execution are as follows:
i == 1100
^ j == 0111
= 1011 == i
j == 0111
^ i == 1011
= 1100 == j
i == 1011
^ j == 1100
= 0111 == i
and the final values assigned to i and j (in the last two statements) clearly show the correct result of the swap. As will be shown next, the self-cancellation property of the xor function also allows the encoding of addresses in order to implement doubly-linked lists without duplication of pointers.
XOR-coded, GDLLs can be represented by a structure containing the usual info field (a genPtr) and an unsigned long integer field called link, whose value will be the xor of two addresses:

In a circular GDLL, every element has a predecessor and a successor. For every node at q such that p and s denote the addresses of its predecessor and successor elements

the assignment q->link = p ^ s allows retrieving the addresses p and s as follows:
Given p and q, p ^ q->link == p ^ p ^ s == s, and given q and s, s ^ q->link == s ^ p ^ s == p.
Thus the link field in every list element "points" to the predecessor and successor elements by encoding their addresses, which is indicated in the figure above by means of the dashed arrows. The fact that given two pointers to logically-adjacent nodes we can retrieve the pointer to the predecessor or the successor of either one of them allows us to implement traversal operations on xor-coded doubly-linked lists (xorDLLs).
In abstract terms, suppose that a list of n data items  has been created using this representation. Let
has been created using this representation. Let  denote the addresses of the elements containing the data items, and let
denote the addresses of the elements containing the data items, and let  and
and  denote the addresses of two additional header elements (containing no useful data, that is NULL pointers, in their info fields). Then, for any node whose address is
denote the addresses of two additional header elements (containing no useful data, that is NULL pointers, in their info fields). Then, for any node whose address is  , for
, for  ,
,
a_{i}->link = a_{i-1 mod(n+2)} \bigoplus a_{(i+1) mod(n+2)}
The following figure illustrates an xorDLL containing three data items, including the two header nodes pointed to by hdr1 and hdr2. Linkage arrows are explicitly shown for the node at address  .
.

An initially empty xorDLL consists exclusively of the two header nodes, whose link fields are equal to 0L. These values indicate that the node at hdr1(hdr2) is both the predecessor and the successor of the node at hdr2(hdr1), as shown below. Alternatively, the node at hdr1(hdr2) is said to be between the node at hdr2(hdr1) and the node at hdr2(hdr1).

In a practical implementation of xorDLLs the following requirements must be met: 1) The list is delimited by two header nodes, 2) The list is traversed starting at the header nodes, and 3) Access to any node requires pointers to two logically-adjacent nodes.
Since xor-coded lists are relatively unknown, I will follow a bottom-up approach to define operations on them. First I will propose a few simple operations which then will be used to implement more complex ones. However, I must emphasize that the code can only be implemented in unmanaged C++. One could be tempted to implement xor-coded lists either in managed C++/CLI or in C# but, since managed code relies on a garbage collector (which moves references to objects during collection), it is impossible (in fact, illegal) to do so.
A minimal xorList can be defined as follows.
typedef void * genPtr;
typedef unsigned long int Dword;
typedef enum { LT, EQ, GT } RelVal;
typedef struct {
genPtr info;
Dword link;
} xorStr;
typedef xorStr * xorPtr;
xorPtr AllocXorStr()
{
xorPtr p = (xorPtr)malloc( sizeof( xorStr ) );
if ( p == NULL ) {
printf( "heap exhausted\n" );
exit( 0 );
}
return p;
}
class xorList {
protected:
xorPtr hdr1, hdr2;
void (*PrnFn)( genPtr, int );
RelVal (*CmpFn)( genPtr, genPtr );
xorPtr Successor( xorPtr, xorPtr );
xorPtr Predecessor( xorPtr, xorPtr );
public:
xorList() { Initialize(); }
~xorList();
void Initialize();
void Dispose();
int IsEmpty();
genPtr OrderedInsert( genPtr );
void Print( int );
genPtr Lookup( genPtr );
};
The constructor xorList calls function Initialize to set up an initially empty list, and to initialize the element-print and element-comparison function pointers.
void xorList::Initialize()
{
PrnFn = NULL; CmpFn = NULL;
hdr1 = AllocXorStr();
hdr2 = AllocXorStr();
hdr1->info = hdr2->info = NULL;
hdr1->link = hdr2->link = 0L;
}
Observe that since the PrnFn and CmpFn pointers are initialized to NULL, xorList behaves as an abstract class, that is, if we create an instance of the class, those functions cannot be invoked without causing an exception. In a class derived from xorList, these pointers must be bound to actual print and comparison functions that deal with the info field of specific xor-coded elements.
The destructor ~xorList must delete all the elements stored in the list. Its definition will be given later, after a few additional functions have been defined. Function xorList::IsEmpty simply determines whether the two header nodes have a link equal to 0L, which means that in an empty xor-coded list, the node at hdr1(hdr2) is between the node at hdr2(hdr1) and the node at hdr2(hdr1).
In order to perform insertions and deletions of elements in xor-coded lists, we can envision some elementary operations that would allow the implementation of complex traversals. Let p and s denote pointers to two logically-adjacent nodes such that the node at p precedes node at s. We can define a protected function Predecessor, to compute the address of the predecessor of the node at p, and a similar function Successor, to compute the address of the successor of the node at s:
xorPtr xorList::Predecessor( xorPtr p, xorPtr s )
{
return (xorPtr)( p->link ^ (Dword)s );
}
xorPtr xorList::Successor( xorPtr p, xorPtr s )
{
return (xorPtr)( s->link ^ (Dword)p );
}
The typecasts of pointers to double words, and double words back to pointers in functions xorList::Predecessor and xorList::Successor are necessary because in C/C++ it is illegal to apply the xor operator (^) to pointers. However, these typecasts are merely explanatory messages to the compiler. In contrast to numeric typecasts (say from int to float) which cause the conversion to take place at run time, pointer typecasts do not cause any explicit conversion at run time. As an illustration, the following figures show the assembly code generated by the Borland C++ compiler under the large model when I implemented non-class versions of equivalent functions pred and succ.


The meaning of the assembly code will be explained in terms of function pred. (A similar reasoning applies to function succ.) The drawing to the left of the assembly code shows the contents of the function’s stack frame during its execution.
The first two instructions save the caller’s base-pointer BP register and set BP to point to the base of the stack frame. The instruction les bx, dword ptr [bp+6] loads in register pair ES:BX the full pointer p (segment:offset) at location BP+6 on the stack. The pointer ES:BX is then used in the next two instructions to access the link field of an xor-coded list structure in two steps: register DX gets the upper word, and register AX gets the lower word. These words constitute a 32-bit number, and they are individually XORed (in the next two instructions) with, respectively, the segment and the offset parts of pointer s at location BP+10 on the stack. Upon return, the function restores the caller’s BP register value and the register pair DX:AX contains the return value of the function, that is, a pointer to the node that logically precedes the node at p.
For comparison, the following is the assembly code generated by Visual Studio 2010 for the unmanaged C++ version of xorList::Predecessor. The interesting assembly code is at line 356 for the return statement, which I have shown in bold. As the reader can verify, there is no type conversion.
; Listing generated by Microsoft (R) Optimizing Compiler Version 16.00.40219.01
TITLE D:\XORstructures\MinGxorList\GxorList.cpp
.686P
.XMM
include listing.inc
.model flat
; COMDAT ?Predecessor@xorList@@IAEPAUxorStr@@PAU2@0@Z
_TEXT SEGMENT
_this$ = -8 ; size = 4
_p$ = 8 ; size = 4
_s$ = 12 ; size = 4
?Predecessor@xorList@@IAEPAUxorStr@@PAU2@0@Z PROC ; xorList::Predecessor, COMDAT
; _this$ = ecx
; 353 : {
push ebp
mov ebp, esp
sub esp, 204 ; 000000ccH
push ebx
push esi
push edi
push ecx
lea edi, DWORD PTR [ebp-204]
mov ecx, 51 ; 00000033H
mov eax, -858993460 ; ccccccccH
rep stosd
pop ecx
mov DWORD PTR _this$[ebp], ecx
; 354 :
; 355 :
; 356 : return (xorPtr)( p->link ^ (Dword)s );
mov eax, DWORD PTR _p$[ebp]
mov eax, DWORD PTR [eax+4]
xor eax, DWORD PTR _s$[ebp]
; 357 : }
pop edi
pop esi
pop ebx
mov esp, ebp
pop ebp
ret 8
?Predecessor@xorList@@IAEPAUxorStr@@PAU2@0@Z ENDP ; xorList::Predecessor
; Function compile flags: /Odtp /RTCsu /ZI
_TEXT ENDS
Having the functions Predecessor and Successor, it is a simple matter to define two additional protected functions to make the pointers to two logically-adjacent nodes move one step either forward or backward in the list:
void xorList::_1stepForward( xorPtr *ap, xorPtr *as )
{
xorPtr p = *ap, s = *as;
*ap = s;
*as = Successor( p, s );
}
void xorList::_1stepBackward( xorPtr *ap, xorPtr *as )
{
xorPtr p = *ap, s = *as;
*ap = Predecessor( p, s );
*as = p;
}
Another useful function to support the implementation of ordered insertions is one to insert a node (pointing to a new data item with its info field) between two logically-adjacent ones. Given pointers to nodes p and s satisfying the assertion p == pred( s, succ( p, s ) ), we can insert a new element, pointed to by q, between them. The following figure illustrates the situations before and after the insertion of such an element. (The existence of the nodes at x and y is guaranteed because the xorList is circular.)

The links stored in the nodes at x and y need not be considered, because such links are not necessary for the insertion. The value p ^ s is stored in the link of the node at q to indicate that such a node is between the nodes at p and s. Because of the insertion of the new element, the links in the nodes at p and s must be updated. The update can be achieved by using only local information in those nodes. To update the link of the node at p, we compute p->link ^ s ^ q. The result, x ^ q, is obtained by the properties of the xor function. To update the link in the node at s, we must compute s->link ^ p ^ q. The protected function to perform the insertion is as follows:
void xorList::InsertBetween( xorPtr q, xorPtr p, xorPtr s )
{
Dword up = (Dword)p, us = (Dword)s, ur = (Dword)q;
q->link = up ^ us;
p->link = p->link ^ us ^ ur;
s->link = s->link ^ up ^ ur;
}
Functions _1stepForward and InsertBetween can now be used to traverse an xorList in the implementation of ordered insertions. The public function receives a genPtr to the object to be stored, and traverses the list looking for the insertion place:
genPtr xorList::OrderedInsert( genPtr gp )
{
RelVal cmp;
xorPtr q, p, s;
p = hdr2;
s = hdr1;
do {
_1stepForward( &p, &s );
} while ( s != hdr2
&&
( cmp = (*CmpFn)( gp, s->info ) ) == GT );
if ( s == hdr2 || cmp != EQ )
{
q = AllocXorStr();
q->info = gp;
InsertBetween( q, p, s );
return gp;
}
else
{
return NULL;
}
}
Observe the use of the function pointer xorList::(*CmpFn) to compare the element being inserted against the element pointed to by s during the traversal of the list. Since the class xorList behaves as an abstract class, CmpFn is bound to NULL in this class and cannot be invoked without being bound to NULL. As will be shown later, when a specific class is derived from xorList, the constructor of the derived class must bind CmpFn (and PrnFn) to non-NULL values. Observe also that the function returns NULL to indicate that the request to insert a duplicate was denied.
A deletion operation can be implemented in a way similar to the insertion of a new element. Given pointers to logically-adjacent nodes p and s such that the assertion p == pred( s, succ( p, s ) ) is satisfied, we can delete one of them, say the one at p. The following figure illustrates the situations before and after the deletion of such an element. (Again, note that the existence of the nodes at x, y, and z is guaranteed because the xorList is circular.) The code implementing the removal is shown after the figure.

genPtr xorList::RemoveAtP( xorPtr p, xorPtr s )
{
xorPtr x;
Dword up;
genPtr gp;
x = Predecessor( p, s );
up = (Dword)p;
x->link = x->link ^ up ^ (Dword)s;
s->link = s->link ^ up ^ (Dword)x;
gp = p->info;
free( p );
return gp;
}
For convenience, function RemoveAtP returns a genPtr to the item that was stored in the info field of the deleted node in order to support removal operations in data structures that will be defined later in terms of xorList. Like function RemoveAtP, a function to remove the node at s can similarly be defined.
genPtr xorList::RemoveAtS( xorPtr p, xorPtr s )
{
xorPtr y;
Dword us;
genPtr gp;
y = Successor( p, s );
us = (Dword)s;
y->link = y->link ^ us ^ (Dword)p;
p->link = p->link ^ us ^ (Dword)y;
gp = s->info;
free( s );
return gp;
}
To print an xor-coded, doubly-linked, circular list, we can use wishful thinking in order to break up the problem into manageable pieces:
void xorList::Print( int brackets = 1 )
{
xorPtr p;
printf( "\n\n" );
PrintHeader( "Header1", hdr1 );
PrintHeader( "Header2", hdr2 );
printf( "\n\n" );
if ( brackets ) { printf( "[ " ); }
p = StartTraversal();
while ( !EndOfTraversal() )
{
PrintElement( p );
p = NextElement();
}
if ( brackets ) { printf( "]" ); }
}
The intention is to print the header nodes on one line, a blank line, and then the list of elements on the following line(s). The protected function xorList::PrintHeader, defined as
void xorList::PrintHeader( char *name, xorPtr headerPtr )
{
printf( "%s: %08lX <!--, %08lX--> ", name, headerPtr, headerPtr->link );
}
prints the header name, its address in hex, and its contents in the format </, link>. The "/" indicates that the info field of a header node is NULL, and the link field is also printed in hex.
The protected function xorList::StartTraversal, defined in terms of xorList::StartForwardScan, starts a forward traversal of the xorList, while function xorList::EndOfTraversal (also protected) determines whether the traversal has gone back to the beginning of the list:
xorPtr xorList::StartTraversal()
{
return StartForwardScan();
}
Functions xorList::StartForwardScan and xorList::EndOfTraversal can be implemented by adding two more protected xorPtr fields to the class
xorPtr E1, succE1,
xorPtr xorList::StartForwardScan()
{
E1 = hdr1;
succE1 = Successor( hdr2, hdr1 );
return succE1;
}
int xorList::EndOfTraversal()
{
return succE1 == hdr2;
}
The protected function xorList::PrintElement prints an element of the list in the format address< info, link >. The address of the node and the link are printed in hex. The info field is printed by calling the function bound to the PrnFn pointer which, as said before, is NULL in the xorList abstract-like class. The PrintFlag is supposed to be a public data member of the class, used to control the printing of a newline after each element.
void xorList::PrintElement( xorPtr p )
{
printf( "%08lX<", p );
(*PrnFn)( p->info, PrintFlag );
printf( ",%08lX>", p->link );
if ( !PrintFlag ) printf( " " );
}
The protected function xorList::NextElement is easily implemented in terms of an auxiliary function MoveForward (also protected) and _1stepForward . The reason for having the auxiliary function will become apparent later.
xorPtr xorList::NextElement()
{
return MoveForward();
}
xorPtr xorList::MoveForward()
{
_1stepForward( &E1, &succE1 );
return succE1;
}
Given the functions that have been developed thus far, the destructor xorList::~xorList can be implemented in a recursive fashion. Consider a typical xor-coded, circular, doubly-linked list, like the following one.

We cannot simply delete a node of this list, for we lose the capability of traversing the list to delete the nodes after the one we deleted. A solution to this problem is first to gain access to all the elements of the list, and then delete them one by one. As is the case with recursive structures, we can rely on the run-time stack used to support recursive executions. The list is traversed as the recursion winds up, setting up pointers to the list elements. The deletion of elements can then be performed when the recursion unwinds.
xorList::~xorList() { Dispose(); }
void xorList::Dispose()
{
DeleteAll( hdr2, hdr1 );
DeleteElement( hdr1 );
}
void xorList::DeleteAll( xorPtr p, xorPtr s )
{
_1stepForward( &p, &s );
if ( s != hdr2 )
{
DeleteAll( p, s );
}
DeleteElement( s );
}
void xorList::DeleteElement( xorPtr p )
{
if ( verbose )
{
printf( "Deleting element: " );
PrintElement( p );
if ( p->info != NULL )
{
printf( " (info at %lX)", p->info );
}
printf( "\n" );
}
if ( p->info != NULL )
{
free( p->info );
}
free( p );
--n;
}
Observe the comment in this function. The deletion of objects pointed to by the info field by means of function free works only if the objects are of primitive type (int, char, float, byte and so on). For more complicated structures, a deletion function must be provided. Function Dispose should be public, while functions DeleteAll and DeleteElement should be protected.
Integer XOR-Coded Lists
In order to manipulate specific instances of xor-coded lists, new classes must be derived from xorList. For example, suppose we wish to maintain an xor-coded list of integers. To this end, we must define functions to print and compare integers pointed to by the info fields (of type genPtr) of the list elements. As indicated before, these functions must be external both to the derived class and to the class xorList. Suitable definitions of these functions are as follows.
typedef int * intPtr;
int icPrnW = 2;
void PrnInt( genPtr gp, int flag )
{
if ( gp != NULL )
{
printf( "%*d", icPrnW, *((intPtr)gp) );
}
else
{
printf( "%*c", icPrnW, '/' );
}
if ( flag )
{
printf( "\n" );
}
}
RelVal CmpInts( genPtr gp1, genPtr gp2 )
{
int i = *((intPtr)gp1), j = *((intPtr)gp2);
return i < j ? LT : i == j ? EQ : GT;
}
Given these functions a class for integer xor-coded lists and a simple test program can be written as follows. (A verbose data member was added to the xorList class to control verbose output.)
class IntXorList : public xorList {
public:
IntXorList()
{
PrnFn = PrnInt; CmpFn = CmpInts;
verbose = 1;
}
};
int _tmain( int argc, _TCHAR* argv[] )
{
int *ip, i;
IntXorList list;
list.Print();
for ( i = 10; i > 6; --i )
{
ip = (int *)malloc( sizeof( int ) );
*ip = i;
list.OrderedInsert( (genPtr)ip );
list.Print();
}
printf( "\n" );
list.Reverse();
printf( "\nReversed list:\n" );
list.Print();
return 0;
}
When built as a console application, the sample test code in function _tmain produces the following output. (To facilitate the verification of links in the list nodes, I have added an xor table for hex numbers.)
Table of hex xor values
| | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 1 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | B | A | D | C | F | E |
| 2 | 2 | 3 | 0 | 1 | 6 | 7 | 4 | 5 | A | B | 8 | 9 | E | F | C | D |
| 3 | 3 | 2 | 1 | 0 | 7 | 6 | 5 | 4 | B | A | 9 | 8 | F | E | D | C |
| 4 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | C | D | E | F | 8 | 9 | A | B |
| 5 | 5 | 4 | 7 | 6 | 1 | 0 | 3 | 2 | D | C | F | E | 9 | 8 | B | A |
| 6 | 6 | 7 | 4 | 5 | 2 | 3 | 0 | 1 | E | F | C | D | A | B | 8 | 9 |
| 7 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | F | E | D | C | B | A | 9 | 8 |
| 8 | 8 | 9 | A | B | C | D | E | F | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 9 | 9 | 8 | B | A | D | C | F | E | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 |
| A | A | B | 8 | 9 | E | F | C | D | 2 | 3 | 0 | 1 | 6 | 7 | 4 | 5 |
| B | B | A | 9 | 8 | F | E | D | C | 3 | 2 | 1 | 0 | 7 | 6 | 5 | 4 |
| C | C | D | E | F | 8 | 9 | A | B | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 |
| D | D | C | F | E | 9 | 8 | B | A | 5 | 4 | 7 | 6 | 1 | 0 | 3 | 2 |
| E | E | F | C | D | A | B | 8 | 9 | 6 | 7 | 4 | 5 | 2 | 3 | 0 | 1 |
| F | F | E | D | C | B | A | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Header1: 00133228 </, 00000000> Header2: 00133260 </, 00000000>
[ ]
Header1: 00133228 </, 000000A8> Header2: 00133260 </, 000000E0>
[ 001332C8<10,00000048> ]
Header1: 00133228 </, 00000150> Header2: 00133260 </, 000000E0>
[ 00133330< 9,000000E0> 001332C8<10,00000150> ]
Header1: 00133228 </, 000001F8> Header2: 00133260 </, 000000E0>
[ 00133398< 8,00000118> 00133330< 9,00000150> 001332C8<10,00000150> ]
Header1: 00133228 </, 00000660> Header2: 00133260 </, 000000E0>
[ 00133400< 7,000001B0> 00133398< 8,00000730> 00133330< 9,00000150> 001332C8<10,00000150> ]
Reversed list:
Header1: 00133228 </, 00000660> Header2: 00133260 </, 000000E0>
[ 00133400<10,000001B0> 00133398< 9,00000730> 00133330< 8,00000150> 001332C8< 7,00000150> ]
~xorList called upon program termination
Deleting element: 00133260< /,000000E0>
Deleting element: 001332C8< 7,00000150> (info at 1333D0)
Deleting element: 00133330< 8,00000150> (info at 133368)
Deleting element: 00133398< 9,00000730> (info at 133300)
Deleting element: 00133400<10,000001B0> (info at 133298)
Deleting element: 00133228< /,00000660>
As expected, when the list is empty, the links in the two header nodes are 0L. After the first element (10) is inserted, its node is between the two header nodes. Therefore the link for this node should be the xor of the addresses of the header nodes, that is, 00133228 ^ 00133260. Using the table, the result is 00000048 which is the value shown in the link field of the node containing number 10. As another example, in the reversed list the node containing 9 is between the nodes containing 10 and 8. Hence, the link of the node containing 9 should be the xor of the addresses of its predecessor and successor nodes, that is, 00133400 ^ 00133330 = 00000730 as shown in the node. The same procedure can be used to verify all the links throughout the insertion process. Observe that the numbers 10 down to 7 were inserted in that order and, since insertions are done in ascending order, function xorList::OrderedInsert inserted them in the proper order.
At the end of the while loop, the list is reversed. Instead of implementing a Reverse function in the derived class, it was implemented in the base class. The algorithm is simple: since the list is doubly-linked and circular, set up pointers to the beginning and end of the list, traverse the list in both directions swapping the contents of the info fields of each pair of nodes, and stop when the traversals reach the middle of the list:
void xorList::Reverse()
{
xorPtr p, q;
genPtr g;
p = StartForwardScan();
q = StartBackwardScan();
while ( !EndOfDualScan() )
{
g = p->info;
p->info = q->info;
q->info = g;
p = MoveForward();
q = MoveBackward();
}
}
Adding two more protected pointer variables to the xorList base class
xorPtr E2, succE2;
the protected auxiliary functions are as follows:
xorPtr xorList::StartForwardScan()
{
E1 = hdr1;
succE1 = Successor( hdr2, hdr1 );
return succE1;
}
xorPtr xorList::StartBackwardScan()
{
E2 = Predecessor( hdr2, hdr1 );
succE2 = hdr2;
return E2;
}
int xorList::EndOfDualScan()
{
return (E1 == E2) || (succE1 == E2);
}
xorPtr xorList::MoveBackward()
{
_1stepBackward( &E2, &succE2 );
return E2;
}
Function xorList::MoveForward has already been written, and function xorList::Reverse is the reason for its existence. Also, function xorList::_1stepBackward has already been written.
Generic, XOR-Coded, Double-Ended Queues
A double-ended queue (deque, pronounced "deck") is a queue that allows enqueue and dequeue operations at both ends. (See G.L. Lipovski Object-Oriented Interfacing to 16-BIT Microcontrollers, Prentice-Hall 1993, pp. 71-73; Mark A. Weiss Data Structures and Algorithm Analysis, Benjamin/Cummings 1992, p. 86 Exercise 3.26 and p. 443 Exercise 11.13; Thomas H. Cormen, Charles E. Leiserson and Ronald L. Rivest Introduction to Algorithms, The MIT Press 1996, p.203 Exercise 11.1-5.) Generic double-ended queues can be implemented in terms of the xorList functionality.
class xorDeck : public xorList {
public:
void EnqueueAtHdr1( genPtr );
void EnqueueAtHdr2( genPtr );
genPtr DequeueFromHdr1();
genPtr DequeueFromHdr2();
};
void xorDeck::EnqueueAtHdr1( genPtr gp )
{
xorPtr r = AllocXorStr();
r->info = gp;
InsertBetween( r, hdr1, Successor( hdr2, hdr1 ) );
}
void xorDeck::EnqueueAtHdr2( genPtr gp )
{
xorPtr r = AllocXorStr();
r->info = gp;
InsertBetween( r, Predecessor( hdr2, hdr1 ), hdr2 );
}
genPtr xorDeck::DequeueFromHdr1()
{
if ( IsEmpty() )
{
printf( "\nThe deck is empty\n" );
return NULL;
}
return RemoveAtS( hdr1, Successor( hdr2, hdr1 ) );
}
genPtr xorDeck::DequeueFromHdr2()
{
if ( IsEmpty() )
{
printf( "\nThe deck is empty\n" );
return NULL;
}
return RemoveAtP( Predecessor( hdr2, hdr1 ), hdr2 );
}
Functions xorDeck::DequeueFromHdr1 and xorDeck::DequeueFromHdr2 provide the reason for functions xorList::RemoveAtS and xorList::RemoveAtP to return a pointer to the element they remove.
Generic, XOR-Coded Stack and Queues
Given the implementation of generic, xor-coded, double-ended queues, it is a simple matter to implement generic stacks and queues as special cases of the xorDeck class.
class xorStack : public xorDeck {
public:
void Push( genPtr gp ) { EnqueueAtHdr1( gp ); }
genPtr Pop() { return DequeueFromHdr1(); }
genPtr Tos();
genPtr Tos_1();
};
genPtr xorStack::Tos()
{
if ( Length() >= 1 )
{
xorPtr q = Successor( hdr2, hdr1 );
return q->info;
}
else
{
printf( "\nThe stack is empty\n" );
return NULL;
}
}
genPtr xorStack::Tos_1()
{
if ( Length() >= 2 )
{
xorPtr q = Successor( hdr1, Successor( hdr2, hdr1 ) );
return q->info;
}
else
{
printf( "\nNot enough elements on the stack\n" );
return NULL;
}
}
Observe that functions xorStack::Tos and xorStack::Tos_1 do not remove stack elements. They merely "peek" at the two top elements of the stack, if they exist. These two functions are very useful for compilers that use an explicit stack to keep track of symbols (see Alfred V. Aho and Jeffrey D. Ullman Principles of Compiler Design, Addison-Wesley 1979, Chapter 5.)
class xorQueue : public xorDeck {
public:
void Enqueue( genPtr gp ) { EnqueueAtHdr2( gp ); }
genPtr Dequeue() { return DequeueFromHdr1(); }
void DeleteLast() { DequeueFromHdr2(); }
int EQtoLast( genPtr );
};
int xorQueue::EQtoLast( genPtr gp )
{
if ( Length() >= 1 )
{
xorPtr r = Predecessor( hdr2, hdr1 );
return (*CmpFn)( gp, r->info ) == EQ;
}
else
{
printf( "\nThe queue is empty\n" );
return NULL;
}
}
Integer XOR-Coded Stacks and Queues
As was done in the case of integer xor-coded lists, integer xor-coded stacks and queues can be implemented, respectively, as specific instances of the xorStack and xorQueue classes. In each case, I will show the definition of the derived class, plus a simple test _tmain function compiled as a console application and followed by the program output (omitting the information printed by the destructor).
class IntXorStack : public xorStack {
public:
IntXorStack()
{
PrnFn = PrnInt; CmpFn = CmpInts;
verbose = 1;
}
};
int _tmain( int argc, _TCHAR* argv[] )
{
int *ip, i;
IntXorStack stack;
stack.Print();
for ( i = 10; i > 6; --i )
{
ip = (int *)malloc( sizeof( int ) );
*ip = i;
stack.Push( (genPtr)ip );
stack.Print();
}
printf( "\n" );
stack.Pop();
stack.Pop();
ip = (int *)malloc( sizeof( int ) );
*ip = 25;
stack.Push( (genPtr)ip );
stack.Print();
printf( "\n" );
return 0;
}
Program output:
Header1: 002F3228 </, 00000000> Header2: 002F3260 </, 00000000>
[ ]
Header1: 002F3228 </, 000000A8> Header2: 002F3260 </, 000000E0>
[ 002F32C8<10,00000048> ]
Header1: 002F3228 </, 00000150> Header2: 002F3260 </, 000000E0>
[ 002F3330< 9,000000E0> 002F32C8<10,00000150> ]
Header1: 002F3228 </, 000001F8> Header2: 002F3260 </, 000000E0>
[ 002F3398< 8,00000118> 002F3330< 9,00000150> 002F32C8<10,00000150> ]
Header1: 002F3228 </, 00000660> Header2: 002F3260 </, 000000E0>
[ 002F3400< 7,000001B0> 002F3398< 8,00000730> 002F3330< 9,00000150> 002F32C8<10,00000150> ]
removing element (at S)002F3228< /,00000660>
removing element (at S)002F3228< /,000001F8>
Header1: 002F3228 </, 00000660> Header2: 002F3260 </, 000000E0>
[ 002F3400<25,00000118> 002F3330< 9,000006C8> 002F32C8<10,00000150> ]
class IntXorQueue : public xorQueue {
public:
IntXorQueue()
{
PrnFn = PrnInt; CmpFn = CmpInts;
verbose = 1;
}
};
int _tmain( int argc, _TCHAR* argv[] )
{
int *ip, i;
IntXorQueue queue;
queue.Print();
for ( i = 10; i > 6; --i )
{
ip = (int *)malloc( sizeof( int ) );
*ip = i;
queue.Enqueue( (genPtr)ip );
queue.Print();
}
printf( "\n" );
queue.Dequeue();
queue.Dequeue();
ip = (int *)malloc( sizeof( int ) );
*ip = 25;
queue.Enqueue( (genPtr)ip );
queue.Print();
printf( "\n" );
return 0;
}
Program output:
Header1: 00523228 </, 00000000> Header2: 00523260 </, 00000000>
[ ]
Header1: 00523228 </, 000000A8> Header2: 00523260 </, 000000E0>
[ 005232C8<10,00000048> ]
Header1: 00523228 </, 000000A8> Header2: 00523260 </, 00000118>
[ 005232C8<10,00000118> 00523330< 9,000000A8> ]
Header1: 00523228 </, 000000A8> Header2: 00523260 </, 000001B0>
[ 005232C8<10,00000118> 00523330< 9,00000150> 00523398< 8,00000150> ]
Header1: 00523228 </, 000000A8> Header2: 00523260 </, 00000628>
[ 005232C8<10,00000118> 00523330< 9,00000150> 00523398< 8,00000730> 00523400< 7,000001F8> ]
removing element (at S)00523228< /,000000A8>
removing element (at S)00523228< /,00000150>
Header1: 00523228 </, 000001F8> Header2: 00523260 </, 000000E0>
[ 00523398< 8,00000628> 00523400< 7,00000150> 005232C8<25,00000660> ]
Running the Code
For the purpose of writing this article, I put all the code under a top-level directory named XORstructures on drive D: of my computer. That directory is contained in the downloadable ZIP file and can be placed anywhere, provided that all the include paths are changed accordingly. Each of the subdirectories (except Common) contains an unmanaged C++ solution, and each solution is a console application. All the code was written, compiled and built using Visual Studio 2010. The solutions, listed in order of dependency, are as follows:
GxorList: Full implementation of generic, doubly-linked, xor-coded lists.
GxorDeck: Full implementation of generic, double-ended queues (depends on GxorList, and supports stacks and queues as special cases).
MinGxorList: Minimal implementation of GxorList (contains the code described in this article).
MinGxorDeck: Implementation of generic, double-ended queues conformant with MinGxorList.
IntXorList: Implementation of integer xor-coded lists (can use either GxorList or MinXorList).
IntXorStack and IntXorQueue: Implementation of integer xor-coded stacks and queues (can use either GxorDeck or MinGxorDeck).
