Frequency Analyser V2.0 - Have you ever wondered what will make tones sound in tune with each other?

• Download BloodShed code - 44.9 KB
• Download source code (VS2003) - 61.3 KB
• Download source code (VS2005) - 62.0 KB

• Download version 2.0 with play functionality (VS2003) - 63.9 KB
• Download version 2.0 with play functionality (VS2005) - 64.4 KB

Introduction

Vibrations, we are surrounded by them and we are making them constantly, shifting the air to communicate. When it comes to music, we have a standard for how they should sound like when they are together and in tune with each other. All we can do is listen to the sounds and see if they are in tune, but why? It would make it easier if we could see what we hear; we need to visualize these tones which will make it easier to analyse them. The sine is a good start to calculate what to visualize. The best way to do this is to use a common machine almost everybody has in their homes, the computer.

To analyze why waves sound good to our ears, we need to be able to take at least two sounds and visualize them. This way we can see what we hear and see the common patterns in these waves. What is already known is that the tone system we use today is built on the twelfth square of two formula and the only real intone sounds are the octaves that are one frequency value split in half or multiplied by two. There are softwares for analyzing waveforms available on the market but the purpose of these programs is not to analyze and learn why sounds are intone with each other. Instead they are more used to record music and make waveforms sound better by the use of filters. Those kinds of software will give you more than you will need here. For analyzing, it would be good to develop a new software that is used for just this single task. Already existing software, as mentioned earlier, are not cheap enough to use for just this purpose. One otherwise good software is Cool Edit from Synthrillium (Adobe audition) and they have a free to use demo trial version, but it is still not useful for analyzing waveforms on this level as needed.

There are plenty of examples from people who have already tried to make this, but they didn't make it exactly shaped for this purpose either. One such example is published here on The site Code Project. This example takes an input signal and transforms it into an equalizer, showing the frequencies extracted from the input signal and transformed by the FFT (Fast Fourier Transform). This software I'm describing in this article is based on a hypothesis that waves do sound better the more they intercept with each other in a time scale. To reject or establish this hypothesis, we need a tool and search for some theories. This project is based on the problem: when not seeing the pattern between tones, why is a C a C and why E an E and why they sound good together. I found in my research that there is a constant multiplied by a frequency of a given tone that will give us the next tone in the scale. This constant is, as mentioned earlier, brought from the twelfth square of two formula were the twelve is the number of tunes in an octave and the number two is half of one octave. An A at 440 Hz is what we have set as the standard note for the starting position in the tone scale. Here we can implement the constant by either multiplying or dividing it with a known tone to get the next half of a tone step up or down. This project and the sample snippets that are included in this document are in C. I've also added a project each for Visual Studio C++ .NET 2003 and 2005. The version 2.0 of this application has a Play function that the first version didn't have.

This article will describe..

• Using the code
• Mixing the waveforms
• DFT - Discrete Fourier Transform
• The Play function
• Points of interest
• Appendix - Pseudo code
• References
• History
• License

Using the code

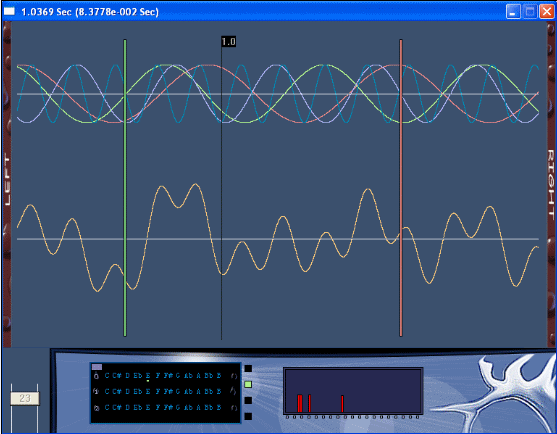
The software is developed in DevC++ (BloodShed) environment in C syntax, with a Win32 API appearance. There are no menus, only mouse events based on where the user clicks in the screen area. The figure shows a screenshot of the demo version; the arrows will point out what it's all about. I have also made a version for VS 2003 and 2005.

1. The title bar shows where the mouse pointer is placed in the view in seconds. And it will also show the time selection between the markers that the user can select by left mouse clicking repeatedly so that two markers will appear, one in red and the other in green.
2. Here are the separate waveforms painted over each other. Visualized in different colors to make it easy to follow one single wave.
3. The ruler shows the user a measurement in time which makes it easy to understand where you are in time.
4. All waves that the user has chosen are mixed together and shown here.
5. User clicks here with the left mouse button to scroll the view about a constant of 0.0625 seconds to the right or to the left if the user clicked on the left side. And if the user clicks with the right mouse button, it will move about 0.5 seconds instead.
6. Zoom bar, can be scaled from 0 to 100 where 50 is half of the usual startup view.
7. Tone board is used to choose which tones you want to analyze. With a right mouse button click in the purple box in the upper left corner of the tone board, the tone will become mute, parked under the purple box. There are 3 octaves to choose from and connect to each tone.
8. Selection of which waveform to be edited on the tone board. As mentioned earlier in this document, there are up to four tones to handle.
9. Frequency domain, which will show the user which frequencies the mixed waveform contains.

Remember - If the user clicks in the waveform view with the right mouse button, the view will scroll to this point. This makes it easy to analyze a specific point in time. There is also a Play button in the newer version 2.0 that will play the mixed sound so that you can here your mix of tones.

Back to top?

Mixing the waveforms

For the calculation of the waveforms, there is the function:

double CalculationZenit(double i, double step, double fq, int type)
{
    if(type==0) return -sin(( i + ( step * HUNDREDS ) * fq ) * DEGREES);
    else if(type==1) 
        return -sin(((i*fq) + ( step * HUNDREDS ) * fq ) * DEGREES);
    else if(type==2) 
        return sin(i*(int)fq * DEGREES);
    return 0;
}

This function takes a value in time (i), a scroll step (step), frequency (fq), and returns a value depending on what the function retrieves in the variable (type). HUNDREDS is a definition to recalculate to hundreds of a second. To mix separate waves together, we use this algorithm:

for(i=0;i<(DEG_SEC*2)/zoom;i=i+(1/zoom/calib))
{
    double temp1 = CalculationZenit(i,step,wH1.freq,1);
    double temp2 = CalculationZenit(i,step,wH2.freq,1);
    double temp3 = CalculationZenit(i,step,wH3.freq,1); 
    double temp4 = CalculationZenit(i,step,wH4.freq,1);
    wHM.rY = temp4 + temp3 + temp2 + temp1; wHM.rX = i*zoom;
    WavePainter (dc, &wHM, RGB(250, 200, 120));
}

This will call WavePainter that will paint the mix on the screen.

void WavePainter(HDC dc, struct WaveHolder *wH, COLORREF rgb)
{ 
    //Check if we need to paint pixel, if we moved one pixel side up or ...
    if((int)wH->rX!=wH->pX||(int)(wH->amp * wH->rY)!=wH->pY)
    {
        wH->pX = (int)(wH->rX);
        wH->pY = (int)(wH->amp * wH->rY);
        SetPixel (dc, wH->sX + wH->rX, wH->sY + wH->amp * wH->rY, rgb );
    }
}

This algorithm loops from 0 to 2 seconds of time and calculates each of the wave form's delta, adding the values together and then putting it on screen by the SetPixel command. wHM is a structure called WaveHolder which holds the information of a wave.

Back to top?

DFT - Discrete Fourier Transform

The following function is the DFT and it is based on the Discrete Fourier Transform formula being used for signal processing that finds all the frequencies in a wave, and it looks like this:

int DFT ( int lenght, double *input, double *output)
{ 
    long i,ii = 1;
    if (NULL==input)
        return ( FALSE );

    for ( i = 1; i < lenght; i++)
    {
        for(ii = 1; ii < lenght; ii++)
        {
            output[i]+= (input[ii]*-sin(i*ii*2*PI/lenght))/length;
        }
    }
    return ( TRUE );
}

Stripped down from the DFT formula, but still can split a waveform into pieces. It takes the length of the data that will be processed and an input buffer that contains this data. It also takes an output buffer where the frequency domain will be stored. What it does is loop through the whole data buffer by a step of 1 with the variable i, and then steps through it again in a nestled loop by the step of 1 with the variable ii. Here, when i is 1 and ii is also 1, it adds the content of field 1 in the input buffer and multiplies it with the negative sin (i*ii*2*PI/length) of the input buffer, and then the sum of this is divided by the length once again. Thus the input value is multiplied by the negative sine of one complete rotation divided by the length, which gives us the frequency domain in the output buffer when it's all done. We divide everything by the length value to normalize it to an acceptable length. If we look closer at the algorithm, we have i multiplied by ii, which will give us these following values when stepping through.

Now if we add the rest of the values inside the negative sin function, we will get:

We must calculate the value of the length; this value is set to 360 in this project, which for us means 1 second in the time scale. If we pretend that the length is 4 and recalculate the previous values, we will get:

If we use these values we have, we can create the fastest frequency we can out of the chosen sample rate. According to Nyquist, the frequency can only be the sample rate / 2; half of 4 Hz sample rate, which in our case gives us the result 2 Hz. The first value when we step through will be 1, second –1, and third will be 1 again, and so on. This is in a 2 Hz frequency. We did this to scale things down and make it possible to calculate and watch what will happen with these values.

Now if we add each row together, we'll get the final result in each field in the output array, which would be:

Half of this result is only needed because of the Nyquist theorem. When i is 1, we have the value of 1 Hz. When i is 2, we have the maximum possible frequency of 2 Hz. Also, note that the value is negative when i is 1 and positive when i is 2, which means that 2 Hz is dominant. This here proves and establishes that the wave we made is made of a 2 Hz frequency. The higher the value shown around i, the more dominant Hertz is around this point. That's the way my stripped down DFT works and is a fast and easy way to analyze frequencies. There's not much more to explain about the code. The rest of the functions are explained in pseudo code in the attachments. They can be found at the end of this document before the References section.

Back to top?

The Play function

Here we have a function implemented in the new version 2.0 that will create a mix of the chosen frequencies and play them:

int PlayIt(struct WaveHolder *wH1,struct WaveHolder *wH2, 
           struct WaveHolder *wH3,struct WaveHolder *wH4)
{
    HWAVEOUT     hWOut; //Handle for sound card
    WAVEHDR      WHeader;//WAVE header
    WAVEFORMATEX WFormat;//The wave format

    char info<BUFFERSIZE>; //Sound data
    HANDLE init_done;

    double x1; //Waves ...
    double x2;
    double x3;
    double x4;

    //Set format
    WFormat.wFormatTag = WAVE_FORMAT_PCM; //Uncompressed
    WFormat.nChannels = 1; //1=Mono 2=Stereo
    WFormat.wBitsPerSample = 8; //8 Bits per sample
    WFormat.nSamplesPerSec = 44100; //Sample per sec
    WFormat.nBlockAlign = WFormat.nChannels * WFormat.wBitsPerSample / 8;
    WFormat.nAvgBytesPerSec = WFormat.nSamplesPerSec * WFormat.nBlockAlign;    
    WFormat.cbSize = 0;

    init_done = CreateEvent (0, FALSE, FALSE, 0);
    
    if (waveOutOpen(&hWOut,0,&WFormat,(DWORD) init_done, 0,CALLBACK_EVENT) != MMSYSERR_NOERROR) 
        return 0;

    double mix;
    
    //Create the mix!
    for(int i=0;i<BUFFERSIZE; i++)
    {
        x1 = sin(i*2.0*PI*((wH1->freq)*OCTAS)/(double)WFormat.nSamplesPerSec); 
        x2 = sin(i*2.0*PI*((wH2->freq)*OCTAS)/(double)WFormat.nSamplesPerSec); 
        x3 = sin(i*2.0*PI*((wH3->freq)*OCTAS)/(double)WFormat.nSamplesPerSec); 
        x4= sin(i*2.0*PI*((wH4->freq)*OCTAS)/(double)WFormat.nSamplesPerSec); 
       
        mix = 128+((x1+x2+x3+x4)*30); //Mix them!
        info[i] = (char)mix;
    }    
    //Put header and sound data together
    WHeader.dwFlags=0;
    WHeader.lpData=info;
    WHeader.dwBufferLength=BUFFERSIZE;
    WHeader.dwFlags=0;
   
    if (waveOutPrepareHeader(hWOut,&WHeader,sizeof(WHeader))!= MMSYSERR_NOERROR)
        return 0;

    ResetEvent(init_done);

    if (waveOutWrite(hWOut,&WHeader,sizeof(WHeader)) != MMSYSERR_NOERROR)
        return 0; //Can't write to card!
    if (WaitForSingleObject(init_done,INFINITE) != WAIT_OBJECT_0)
        return 0; //Could not wait anymore!

    //Disconnect.
    if (waveOutUnprepareHeader(hWOut,&WHeader,sizeof(WHeader))!= MMSYSERR_NOERROR)
        return 0;

    //Shut down device.
    if (waveOutClose(hWOut) != MMSYSERR_NOERROR)
        return 0;

    //Close handle!
    CloseHandle(init_done);
}

The project runs mainly on a Pentium 4 3.2 GHz Intel processor when it is tested, but can also run in other environments like Windows 2000 and NT. All of the tests were made on a PC with a Windows Operating System. The BloodShed version in C uses about 2 MB RAM memory and approximately 400-KB disk space. Most of the RAM usage is caused by the graphics, that uses 372 KB of disk space. The SetPixel GDI function takes machine time when it is called and the algorithms that are using this function had to be rearranged/optimized so that we could reduce this time when painting higher frequencies.

Back to top?

Points of interest

If there will be a next version of this software, there will be better structuring of the code, using more structures and functions. One of the findings was that it's hard to make a software of this size without having the constant problem of changing the whole code when changing a small piece somewhere in it. When it comes to the point of using the software, a test subject must put time and effort into this. If the complete mix down has rhythms in time, it shows a more intone result than the sounds that are in contrary to this. And when it comes to the software, it might have some leaks for the moment, but this will be solved before it's completed.

The most enlightening thing about this is that you can change the frequencies fast, which is timesaving when analyzing. The Fourier Transform in this project is a bit unnecessary here because it's not fully used, the frequencies are already known from the beginning. But this is a function ready to implement and develop in the next version when a loading function will be present to let the user analyze .wav files. The project is most useful as a learning tool, a fast way to analyze the tones you're playing on a guitar or piano etc.

This version is limited in function when it comes to how many tones you're able to analyze at the same time; in a guitar accord, you use up to 6 tones if the guitar has 6 strings. Here you only have 4 tones to deal with, but it would anyhow be like a maze to look at more tones than 4 if it's drawn over each other on the screen. One other thing to mention is that the software needs a three button mouse with a wheel button installed to work; the wheel is needed to scale/zoom the waveforms up or down. The purpose of this software is achieved at the point that it can visualize the sound, but you should try it out to find out if it's working like it is meant to do.

Back to top?

Appendix

Here is the pseudo code for the project, starting with the structures.

STRUCTURE CLICKER 
s1Marked; 
s1Tone; 
s2Marked; 
s2Tone; 
s3Marked; 
s3Tone; 
s4Marked; 
s4Tone; 
STRUCTURE – END 

STRUCTURE WAVEHOLDER 
freq; 
amp; 
sX; 
sY; 
rX; 
rY; 
pX; 
pY; 
STRUCTURE – END 

FUNCTION INITWINDOW 
Input variables - hInstace 
Local variables - hwnd, wincl. 
SET - A winddowclass 
IF - it fails 
RETURN - 0 
IF - END 
CREATE – A window. 
RETURN – hwnd. 
FUNCTION – END 

FUNCTION STEERINGMOTOR 
Input variables – hwnd, msg,zoom,step,x,y,cSTRUCTURE clicko,done 
Local variables – r,sender 
IF – mouse move 
Calculate and transform mouse coordinates into time. 
DISPLAY – coordinates in titelbar. 
IF – END 
IF – mousewheel 
Transform wheel delta into zoom value. 
END _ IF 
IF – left mouse button down 
IF – mouse pointer is within the left scroll area. 
DECREASE – variable step by 6.25. 
ELSE – IF – mouse button is within the right scroll area. 
INCREASE – variable step by 6.25 
ELSE – IF – mouse pointer is within first frequency button. 
SELECT – frequency or deselect. 
ELSE – IF – mouse pointer is within second frequency button. I 
SELECT – frequency or deselect. 
 
ELSE – IF – mouse pointer is within third frequency button. 
SELECT – frequency or deselect. 
ELSE – IF – mouse pointer is within fourth frequency button. 
SELECT – frequency or deselect. 
ELSE - IF – END 
IF – mouse is within the toneboard 
SET – a new higheer position on the marker by one half tone step.
 To indicate that a new tone has been given. 
IF – END 
IF – right mouse button down 
IF – mouse pointer is within the left scroll area. 
DECREASE – variable step by 50.0 
ELSE – IF – mouse pointer is within the right scroll area. 
INCREASE – variable step by 50.0 
ELSE – IF –END 
END – IF 
IF – mouse pointer is within the scroll view 
INCREASE – variable step as mutch as needed to make the view scroll
 to the chosen point. 
END – IF 
IF – mouse is within tone board area 
SET – the tone board marker to a new lower tone by a half tone step. 
IF – END 
FUNCTION – END 

FUNCTION – PAINTRECT 
Input variables – dc,x1,y1,x2,y2,rgb 
Local variables – old,br 
CREATE – create a brush with the color stored in the rgb variable. 
DISPLAY – The box on the screen at given cordinates. 
FUNCTION - END 

FUNCTION WAVEPAINTER 
Input variable – dc,STRUCTURE wH, rgb 
IF – it's a new point, then it´s time to paint. 
DISPALY – pixel on the screen. 
IF – END 
FUNCTION – END 

FUNCTION PAINTRULER 
Input variable – dc, zoom,step,discount 
Local variable – meter,o 
LOOP – While o is less than 2 seconds of time. 
IF – One second of time has elapsed. 
DISPLAY – a line over this point in vertical direction. 
IF - END 
LOOP – END 
FUNCTION – END 

FUNCTION – PAINTGRAPHIX 
Input variable – hwnd,zoom,step,fout,foutimg,done,discount,STRUCTURE clicko 
Local variable – dc,ps, wH1,wH2,wH3,wH4.wHM,o,i,time,c0,calib 
SET – wH1 to wH4 by a tone frequency and amplitude. 
IF – a frequency is unselected. 
SET – this frequency to 0. II 
IF – END 
 SET – the highest frequency to the variable calib. 
LOOP – trough 2 seconds of time. 
FUNCTION CALL – Call the CALCULATIONZENTIT function. 
SET – wH1 to wH4 whit the return value from previous function call. 
DISPLAY – all four waveforms. 
LOOP – END 
LOOP – trough 2 seconds of time. 
FUNCTION CALL – Call the CALCULATIONZENIT function. 
CALCULATE – the complete mix by the four wasveforms. 
DISPALY – te mixdown of waves. 
LOOP – END 
IF – if this is not yet done. 
SET – variable done to 1 to indicate it's done. 
LOOP – one half second of time. 
SET – DFT field with wave info. 
LOOP – END 
IF – END 
DISPLAY – all bitmap graphics and frequency domain, and the ruler. 
FUNCITON – END 

FUNCTION – TONEBOARDMARKER 
Input variables – dc,clicko 
Local variables – x,y,temp,cR 
DISPLAY – the four frequency buttons and the tone board marker. 
FUNCTION – END 
FUNCTION – DFT 
Input variable – length,input,output 
Local variable – i,ii 
IF – input field is NULL 
RETURN – FALSE 
IF – END 
LOOP – from 1 to variable length by the step of one in variable i. 
LOOP - from 1 to variable length by the step of one in variable ii. 
CALCULATE – the DFT values in the output buffer. 
LOOP – END 
RETURN – the value TRUE. 
LOOP – END 
FUNCTION – END 

FUNCTION – CACULATIONZENIT 
Input variables – i,step,fq,type 
IF – type is 0 
RETURN - -sin((i+(step*HUNDREDS)*fq)*DEGREES) 
IF – END 
IF type is 1 
RETURN - -sin(((i*fq)+(step*HUNDREDS)*fq)*DEGREES) 
IF – END 
IF – type is 2 
RETURN – sin (i*(int)fq*DEGREES) 
IF – END 
RETURN – 0 
FUNCTION – END 
Input variables – hBitmap 
LOAD – a bitmap and store it. 
RETURN – hBitmap 
FUNCTION – END 

FUNCTION – PAINTBITMAP 
Input variables – dc,hBitmap,x1,y1,width,height 
DISPLAY – bitmap on the screen. 
FUNCTION – END

Back to top?

References

Works of reference

• Bilting, Skansholm "Vagen till C" – ISBN: 91-44-01460-6
• Kochan G. S. "Programming in C" – Third Edition – ISBN: 0-672-32666-3
• LaMothe, André "Tricks of the windows programming gurus" – ISBN: 0-672-31361-8
• Svardstrom, Anders "Tillampad signalanalys" – ISBN: 91-44-25391-5

Links

• Adobe Audition 2.0.
• FFT of waveIn audio signals - By Fred Ackers.
• Written by Paul Bourke June 1993.
• "A = 440Hz - men varfor?" av Paul Guy
• Half Steps and Whole Steps By: Catherine Schmidt-Jones
• Anti-Aliased Line Drawing
• The C Programming Language.

Back to top?

History

• Version 1.0: Uploaded ? November, 2007 - Version one, had no Play function.
• Version 2.0: Uploaded 26 November, 2007 - A Play function was implemented.
• Version *: Updated 30 November, 2007 - Made a few changes to the article.

Back to top?

License

This software is provided 'as-is' without any express or implied warranty. In no event will the author(s) be held liable for any damages arising from the use of this software. Permission is granted to anyone to use this software for learning purpose only. And never could you claim that it is yours.