Distributed Caching Using a Hash Algorithm

Introduction

This article presents an idea for a hashing algorithm that can be used in distributed caching of data in web farms or implementing a distributed hash table (DHT)

The Algorithm

Using state or caching data in memory is usually a problem in high volume web sites because it is difficult to scale. Out-of-the-box ASP.NET offers three ways of storing session information – in process, out of process and using a database but none of them can be easily scaled out. In addition, using a database for storing session state is quite expensive.

Ideally for session management in a large scale web application, we should be able to "plug-in" relatively low spec "cache machines" and have an infrastructure that spreads evenly the data to be cached across the whole pool. The diagram below illustrates what I am referring to.

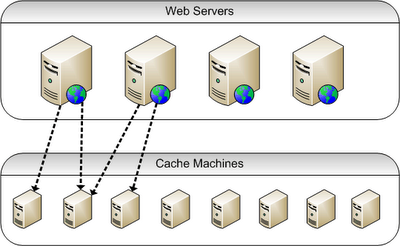
We have a layer of web servers that handle the requests and a pool of machines that are used for caching. Each web server should be able to access any of the cache machines. The tricky aspect here is that when we cache some data as a result of a request to a particular web server, we should be able to retrieve that data from any of the other web servers.

After doing some searching, I came across Memchached, which uses a hashing mechanism to distribute the cached data across the pool of cache machines and also provides a reliable way of retrieving the data. That's what prompted me to try and develop a similar algorithm in C# that can be used in such a scenario.

There are two features that we can benefit from if we use hashing for this type of solution. First of all, when we hash a piece of data the resulting bit array is always of the same length. Secondly, I am not sure if this is applicable to all hashing algorithms but the produced hashes are statistically random so we may assume that they form some kind of a uniform distribution.

Here is what we can do. We want to cache key value pairs and then at a later stage get hold of a cached value by providing the corresponding key. The code below takes a key and produces a hash bit array using SHA1. Then after some transformations we derive an integer number. A given key always produces the same number. In addition, all numbers are uniformly distributed which allows us to "page" them and assign them to a given number of cache machines or "buckets".

With this algorithm, we ensure that each key will always point to the same bucket and all keys will be evenly spread across the pool of cache machines.

KeyDistributor Class

public class KeyDistributor<TKey>
{
    private int _numBuckets;
    private int _pageSize;
    private SHA1 _sha;

    public int CalculateBucketIndex(TKey key)
    {
        if (_numBuckets == 1)
        {
            return 0;
        }

        // Create a SHA1 hash of the provided key
        byte[] result;
        byte[] data = BitConverter.GetBytes(key.GetHashCode());
        result = _sha.ComputeHash(data);

        // Split the hash into 4 integer numbers
        uint n1 = BitConverter.ToUInt32(result, 0);
        uint n2 = BitConverter.ToUInt32(result, 4);
        uint n3 = BitConverter.ToUInt32(result, 8);
        uint n4 = BitConverter.ToUInt32(result, 12);
        uint n5 = BitConverter.ToUInt32(result, 16);

        // Apply XOR to derive a combined number
        uint index = n1 ^ n2 ^ n3 ^ n4 ^ n5;

        // Calculate the bucket index
        int bucketIndex = Convert.ToInt32(Math.Floor((double)(index / _pageSize)));

        return bucketIndex;
    }

    public KeyDistributor(int numBuckets)
    {
        _numBuckets = numBuckets;

        if (_numBuckets > 1)
        {
            // Based on the number of buckets calculate the page size.
            // It will be to link a given key to a specific bucket
            _pageSize = Convert.ToInt32
			(Math.Ceiling((double)(uint.MaxValue / numBuckets)));
            _sha = new SHA1Managed();
        }
    }
} 

Testing the Code

Let's now test this algorithm. The static method below creates a number of buckets and caches items in them. Each item is a key-value pair where the key is a GUID.

static void Main(string[] args)
{
    // The number of items to cache
    int k = 10000;
    // The number of buckets
    int bucketsNum = 8;
    List<Dictionary<Guid, string>> buckets = new List<Dictionary<Guid, string>>();
    List<Guid> values = new List<Guid>();

    // Initialize the buckets
    for (int i = 0; i < bucketsNum; i++)
    {
        buckets.Add(new Dictionary<Guid, string>());
    }

    // Create an instance of the KeyDistributor class
    KeyDistributor<Guid> kd = new KeyDistributor<Guid>(bucketsNum);

    for (int i = 0; i < k; i++)
    {
        // Create a Guid type of key
        Guid guid = Guid.NewGuid();
        // Calculate the bucket index
        int bucketIndex = kd.CalculateBucketIndex(guid);
        // Cache the item in the bucket
        buckets<bucketindex>.Add(guid, guid.ToString());
        // Add the key to a list so that we can later retrieve corresponding value
        values.Add(guid);
    }

    // Display the number of items in each bucket
    for (int i = 0; i < buckets.Count; i++)
    {
                Console.WriteLine("Bucket " + i + ": " + buckets[i].Count);
    }

    // Retrieve each cached item. This is to check that we can get hold of
    // each cached item
    for (int i = 0; i < values.Count; i++)
    {
        Guid guid = values[i];
        int bucketIndex = kd.CalculateBucketIndex(guid);
        string val = buckets<bucketindex>[guid];

        // If the item is not found raise an error
        if (String.IsNullOrEmpty(val))
        {
            throw new Exception("Cached item cannot be found");
        }
    }

    Console.ReadLine();
} 

These are the results:

Number of buckets 3, items to cache 10,000.
Bucket 0: 3297
Bucket 1: 3342
Bucket 2: 3361

Number of buckets 8, items to cache 1,000,000.
Bucket 0: 125195
Bucket 1: 125419
Bucket 2: 124767
Bucket 3: 125105
Bucket 4: 124933
Bucket 5: 125086
Bucket 6: 125045
Bucket 7: 124450

As it can be seen, the distribution of items is almost even across the pool of buckets. The code does not raise any errors, which means that we can successfully retrieve each cached item.

Next Steps

In another article, I will illustrate a complete distributed caching prototype using named pipes.

History

• 1^st December, 2007: Initial post