Basic Recursion
The intention of this article is to explain the basics of algorithms through the use of basic recursion. Later on, we will look at how data structures relate to stacks and queues. This article, however, is partly referenced from Kyle Loudon's book "Mastering Algorithms with C". But in general, the correctly-chosen algorithm will solve problems and are basically a computational model that uses data structures and abstractions. These help to itemize data via list data, sort data, stack data, queue data, list data on a linked list, and so on. When writing an algorithm to solve a problem, one must break down that problem into its constituent parts. This is why recursion is important. Recursion allows something to be defined in terms of itself. That is, a recursive function will call itself. In computing, recursion is supported via recursive functions. Each successive call works on a more refined set of inputs, bringing us closer to the solution of the problem. Visualize the number of core rings on a sawn tree trunk. They primarily have the same shape, and get smaller and smaller to help scientists calculate the age of the tree. If one is faced with a computational problem, then an important choice the developer has to figure out is how to partition the original problem into individual sub-parts to then write functions to solve them. This will be evidenced in the code examples given. Having said that, let's explore how recursion works to show how to define some problems in a recursive manner.
Basic recursion is a principle that allows a problem to be defined in terms of smaller and smaller instances of itself. In computing, we solve problems defined recursively by using recursive functions, which, again, are functions that call themselves. To begin, let's consider a simple problem that normally we might not think of in a recursive way. Suppose we could like to compute the factorial of a number n. The factorial of n, written n!, is the product of all numbers from n down to 1. For example, 4! = (4)(3)(2)(1). One way to calculate this is to loop through each number and multiply it with the product of the preceding numbers. This is an iterative approach, which can be defined more formally as:
n! = (n)(n - 1)(n - 2) . . . (1)
Another way to look at this problem is to define n! as the product of smaller factorials. To do this, we define n! as n times the factorial of n-1. Of course, solving (n-1)! is the same problem as n!, only a little smaller. If we then think of (n-1)! as n-1 times (n-2)!, as n-2 times (n-3)!, and so forth until n = 1, we end up computing n!
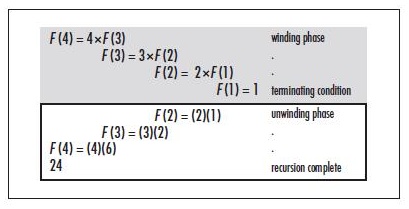
The figure below illustrates computing 4! using the recursive approach just described. It also delineates two basic phases of the recursive process: winding and unwinding. In the winding phase, each recursive call perpetuates the recursion by making an additional recursive call to itself. The winding phase terminates when one of the calls reaches a terminating condition. A terminating condition defines the state at which a recursive function should return instead of making another recursive call. For example, in the computing of factorial of n, the terminating conditions are n = 1 and n = 0, for the function simply returns 1. Every recursive function must have at least one terminating condition. Otherwise, the winding phase never terminates. Once the winding phase is complete, then process the unwinding phase in which the previous instances of the function are revisited in reverse order. The phase completes until the original call returns, at which point the recursive process is complete.
Tail recursion is a form of recursion for which compilers are able to generate optimized code. Most modern compilers recognize tail conversion, and should therefore be capitalized on. Here is a sample code, with user-defined header files to exemplify the recursion principle in a factorial computation:
#ifndef FACT_H
#define FACT_H
int fact(int n);
#endif
The next user-defined header file
#ifndef FACTTAIL_H
#define FACTTAIL_H
int facttail(int n, int a);
#endif
These header files should be copied and pasted into the include directory of whatever version of VC++ you are using. Now, here are those files that implement the functions in the header files. Recall that these functions were written to solve the problem that will be broken into a "basic" recursion" and "tail" recursion.
#include "fact.h"
int fact(int n) {
if (n < 0)
return 0;
else if (n == 0)
return 1;
else if (n == 1)
return 1;
else
return n * fact(n - 1);
}
Here is the second file that implements the functions defined in its corresponding header file:
#include "facttail.h"
int facttail(int n, int a) {
if (n < 0)
return 0;
else if (n == 0)
return 1;
else if (n == 1)
return a;
else
return facttail(n - 1, n * a);
}
The above two C source files compile into object files. They define the two functions written to handle the parts of the divided problem. They will be linked to the main file when the main is compiled. We'll do this on the command line to gain a sharper understanding. Below is the main program, called main.c, that contains the main-entry point. Note that this file will not compile without being linked to the two above files. Those files are compiled using the /LD switch of the Visual Studio 2008 cl.exe compiler (or the command line configuration property of the project property page). Using this switch means that the above two files compile as DLLs, but are linked to this main file as object files:
#include <stdio.h>
#include "fact.h"
#include "facttail.h"
int main(int argc, char **argv) {
int n;
for (n = 0; n <= 13; n++) {
fprintf(stdout, "%2d! recursive: %-10d ", n, fact(n));
fprintf(stdout, "tail recursive: %-10d\n", facttail(n, 1));
}
return 0;
}
OK. So we have two user-defined header files, two files that define what is in those header files, and a main program that will not compile without linking to those definition files. A common question would be the fprintf() function. The fprintf() function writes formatted output to an open file. Here is an example:
#include <stdio.h>
#include <time.h>
int main(int argc, char *argv[])
{
FILE *fp_log;
time_t sec;
fp_log = fopen("example.log", "a");
if (fp_log != NULL)
{
time(&sec);
fprintf(fp_log, "%.24s Opened lg file.\n", ctime (&sec) );
}
return 0;
}
Output: Check the bin directory of the command line for the VS 2008 cl.exe compiler and you will find a file called example.log. Open it with Notepad and it will say:
Sat Mar 06 05:35:35 2010 Opened log file.
Now we want to compile these algorithm files. We know to add those user-defined header files to the include directory. Remember to run the vcvars32.bat command to set the environment prior to any attempt at compiling. The command 'type con > some_file.c gives you a blank screen with a cursor. Copy and paste these files into that blank screen, and then press the Control-Z keyboard combination to terminate the file and return to the prompt.
#include "fact.h"
int fact(int n) {
if (n < 0)
return 0;
else if (n == 0)
return 1;
else if (n == 1)
return 1;
else
return n * fact(n - 1);
}
^Z
C:\PROGRA~1\MICROS~1.0\VC\bin>cl /LD fact.c
Microsoft (R) 32-bit C/C++ Optimizing Compiler Version 15.00.30729.01 for 80x86
Copyright (C) Microsoft Corporation. All rights reserved.
fact.c
/out:fact.dll
/dll
/implib:fact.lib
fact.obj
C:\PROGRA~1\MICROS~1.0\VC\bin>type con > facttail.c
#include "facttail.h"
int facttail(int n, int a) {
if (n < 0)
return 0;
else if (n == 0)
return 1;
else if (n == 1)
return a;
else
return facttail(n - 1, n * a);
}
^Z
C:\PROGRA~1\MICROS~1.0\VC\bin>cl /LD facttail.c
Microsoft (R) 32-bit C/C++ Optimizing Compiler Version 15.00.30729.01 for 80x86
Copyright (C) Microsoft Corporation. All rights reserved.
facttail.c
Microsoft (R) Incremental Linker Version 9.00.30729.01
Copyright (C) Microsoft Corporation. All rights reserved.
/out:facttail.dll
/dll
/implib:facttail.lib
facttail.obj
C:\PROGRA~1\MICROS~1.0\VC\bin>type con > main.c
#include <stdio.h>
<stdio.h />#include "fact.h"
#include "facttail.h"
int main(int argc, char **argv) {
int n;
for (n = 0; n <= 13; n++) {
fprintf(stdout, "%2d! recursive: %-10d ", n, fact(n));
fprintf(stdout, "tail recursive: %-10d\n", facttail(n, 1));
}
return 0;
}
^Z
C:\PROGRA~1\MICROS~1.0\VC\bin>cl main.c /link fact.obj facttail.obj
Microsoft (R) 32-bit C/C++ Optimizing Compiler Version 15.00.30729.01 for 80x86
Copyright (C) Microsoft Corporation. All rights reserved.
main.c
Microsoft (R) Incremental Linker Version 9.00.30729.01
Copyright (C) Microsoft Corporation. All rights reserved.
/out:main.exe
fact.obj
facttail.obj
main.obj
Output:
C:\PROGRA~1\MICROS~1.0\VC\bin>main.exe
0! recursive: 1 tail recursive: 1
1! recursive: 1 tail recursive: 1
2! recursive: 2 tail recursive: 2
3! recursive: 6 tail recursive: 6
4! recursive: 24 tail recursive: 24
5! recursive: 120 tail recursive: 120
6! recursive: 720 tail recursive: 720
7! recursive: 5040 tail recursive: 5040
8! recursive: 40320 tail recursive: 40320
9! recursive: 362880 tail recursive: 362880
10! recursive: 3628800 tail recursive: 3628800
11! recursive: 39916800 tail recursive: 39916800
12! recursive: 479001600 tail recursive: 479001600
13! recursive: 1932053504 tail recursive: 1932053504
Stack Winding and Unwinding
Return to the simple example of 4!. That is, 4 * 3 * 2 * 1 = 24. The recursive approach defined also delineates two basic phases: winding and unwinding. In the winding phase, each recursive call perpetuates the recursion by making an additional recursive call itself. The winding phase terminates when one of the class reaches a terminating condition. A terminating condition defines the state at which a recursive function should return instead of making another recursive call. This is basically stack unwinding. When the function is called, a stack is allocated to push the function's parameters onto the stack while the function performs a task. The function completes the task (ideally) and then takes the path of return to the return address, also on the stack. The instruction pointer (CS:IP) register points at the next instruction that follows. In fact, this is one way to really understand recursion: by taking a look at the way functions are executed in the C language. For this, it helps to understand about the organization of a C program in memory.
Program memory is divided into four segments: code (text) area , static data area, heap, and stack. Each segment represents a special portion of memory that is set aside for a certain purpose. The static data segments are used to store global and static program variables. The data segment is filled with the initialized global variables, strings, and other constants that are used through the program.. Although these segments are writable, they also have a fixed size.
The heap segment is used for the rest of the program variables. One notable point about the heap segment is that it isn't of fixed size, meaning it can grow larger or smaller as needed.
The stack segment also has variable size and is used as a temporary scratchpad to store context during function calls. When a program calls a function, that function will have its own set of passed variables, and the function's code will be at a different memory location in the text (or code) segment. Because the context and the EIP must change when a function is called, the stack is used to remember all of the passed variables and where the EIP should return to after the function is finished.
A stack is an abstract data structure that is used frequently. It has first-in, last-out (FILO) ordering, which means the first item that is put into a stack is the last item to come out of it. Like putting beads on a piece of string that has a giant knot on the end, you can't get the first bead off until you have removed all the other beads. When an item is placed into a stack, it's known as pushing, and when an item is removed from a stack, it's called popping.
This small code segment first declares a test function that has four arguments, which are all declared as integers: a, b, c, and d. The local variables for the function include a single character called flag and a 10-character buffer called buffer. The main function is executed when the program is run, and it simply calls the test function. When our_function is called from the main function, the various values are pushed to the stack to create the stack frame as follows. When our_function() is called, the function arguments are pushed onto the stack in reverse order (because it's FILO). The arguments for the function are 1, 2, 3, and 4, so the subsequent push instructions push 4, 3, 2, and finally 1 onto the stack. These values correspond to the variables d, c, b, and a in the function.
#include <stdlib.h>
void our_function(int a, int b, int c, int d)
{
char flag;
char buffer[10];
}
void main()
{
our_function(1, 2, 3, 4);
}
Suffice it to say that the code area runs the machine instructions that are executed as the machine runs. The static data area contains data that persists through the life of the program, such as global variables and local static variables. Now when a function is called in a C program, a block of storage is allocated on the stack to keep track of information associated with the call. Each call is referred to as activation. The block of storage placed on the stack is called an activation record or, alternatively, a stack frame. An activation record consists of five regions: incoming parameters, space for a return value, temporary storage used in evaluating expressions, saved state information for when the activation terminates, and outgoing parameters. Incoming parameters are the parameters passed into the activation. Outgoing parameters are the parameters passed to functions called within the activation. The outgoing parameters of one activation record become the incoming parameters of the next one placed on the stack. The activation record for a function call remains on the stack until the call terminates. Now consider what happens when one computes 4!:
The call to fact results in one activation record being placed on the stack with an incoming parameter of n = 4. Since this activation record does not meet any of the terminating conditions of the function, fact is recursively called with n = 3. This places another activation of fact on the stack, but with an incoming parameter of n = 3. Here, n = 3 is also an outgoing parameter of the first activation since that activation invoked the second activation. The process continues until n = 1, where a terminating condition is encountered and fact returns 1. Once the n = 1 activation terminates, the recursive expression in the n = 2 activation is evaluated a (2)(1) = 2. Consequently, the recursive expression in the n = 3 activation return 6. Finally, the recursive expression in the n = 4 activation is evaluated as (4)(6) = 24 and the n = 4 activation terminates with a return value of 24. At this point, the function has returned from the original call, and the recursive process is complete.
Stacks & Queues
Now we will, for the sake of proof of concept, explore stacks and queues. The reader may wonder why I am not using a language like C#, Java, Visual C++, or ISO C++. The reason is that C was the first language ever used to write an Operating System. It was written by Dennis Ritchie and Brain Kernaum as a solution to the B language. C was not written during the Internet age and was therefore not considered a security threat. It was written to write the UNIX system, and later the Windows system. C compiles directly down to machine-level code, which outputs an object (module) file (or a resource file). The headers are comprised of predefined functions, in which the type of the function is of the type of the name of the header file. The C library is static, and the linker links the object file to the source code file in order to build the executable by copying those predefined functions onto the building of the executable. If these functions were not predefined, then their definitions would then involve a string extraction process through a hardware I/O port, a process that would take longer than writing the program and compilation. But if the underlying principles of algorithms can be understood, then they can be transferred to more powerful languages like C# for serious problem solving. They can also result in solutions that use the powerful .NET graphics.
Recall the activation record. Earlier we used the term data structure. It is important to store data so when it is retrieved later, it is automatically presented in some prescribed order. One way to retrieve data is in the opposite order as it was stored. For example, consider the data blocks a program maintains to keep track of function calls as it runs. As we have just seen, these blocks are called activation records. For a set of functions {f1, f2, f3} in which f1 calls f2 and f2 calls f3, a program allocates one activation record each time one of the functions is called. Each record persists until its function returns. Since functions return in the opposite order as they were called, activation records are retrieved and relinquished in the opposite order as they were allocated. Another common way to retrieve data is in the same order as it was stored. For example, this might be useful with a bunch of things to do; often we want to do the first item first and the last item last. Stacks and queues are simple data structures that help store data in a way that is predefined according to the needs. Stacks are abstract data structures for storing and retrieving data in a last-in first-out way. Queues are data structures useful for storing data structures in a first-in first-out (FIFO) order.
Here is some code that should be examined in correlation with the explanation of the stack's pushing and popping functions. There are two user-defined header files, stack.h and list.h, along with three source files: stack.c, list.c, and main_stack.c. The latter file contains the main point of entry. The two previous files must be compiled as modules, yet are both interdependent on each other to compile prior to compiling the main_stack.c file. These two header files can be copied and pasted to the include directory of whatever version of Visual Studio you are using:
#ifndef LIST_H
#define LIST_H
#include <stdlib.h>
typedef struct ListElmt_ {
void *data;
struct ListElmt_ *next;
} ListElmt;
typedef struct List_ {
int size;
int (*match)(const void *key1, const void *key2);
void (*destroy)(void *data);
ListElmt *head;
ListElmt *tail;
} List;
void list_init(List *list, void (*destroy)(void *data));
void list_destroy(List *list);
int list_ins_next(List *list, ListElmt *element, const void *data);
int list_rem_next(List *list, ListElmt *element, void **data);
#define list_size(list) ((list)->size)
#define list_head(list) ((list)->head)
#define list_tail(list) ((list)->tail)
#define list_is_head(list, element) ((element) == (list)->head ? 1 : 0)
#define list_is_tail(element) ((element)->next == NULL ? 1 : 0)
#define list_data(element) ((element)->data)
#define list_next(element) ((element)->next)
#endif
And here is the second header file, stack.c:
#ifndef STACK_H
#define STACK_H
#include <stdlib.h>
#include "list.h"
typedef List Stack;
#define stack_init list_init
#define stack_destroy list_destroy
int stack_push(Stack *stack, const void *data);
int stack_pop(Stack *stack, void **data);
#define stack_peek(stack) ((stack)->head == NULL ? NULL : (stack)->head->data)
#define stack_size list_size
#endif
The other header files come with any version of Visual C++. Here is the list.c file:
#include <string.h>
#include <stdlib.h>
#include "list.h"
void list_init(List *list, void (*destroy)(void *data)) {
list->size = 0;
list->destroy = destroy;
list->head = NULL;
list->tail = NULL;
return;
}
void list_destroy(List *list) {
void *data;
while (list_size(list) > 0) {
if (list_rem_next(list, NULL, (void **)&data) == 0 &&
list->destroy != NULL) {
list->destroy(data);
}
}
memset(list, 0, sizeof(List));
return;
}
int list_ins_next(List *list, ListElmt *element, const void *data) {
ListElmt *new_element;
if ((new_element = (ListElmt *)malloc(sizeof(ListElmt))) == NULL)
return -1;
new_element->data = (void *)data;
if (element == NULL) {
if (list_size(list) == 0)
list->tail = new_element;
new_element->next = list->head;
list->head = new_element;
}
else {
if (element->next == NULL)
list->tail = new_element;
new_element->next = element->next;
element->next = new_element;
}
list->size++;
return 0;
}
int list_rem_next(List *list, ListElmt *element, void **data) {
ListElmt *old_element;
if (list_size(list) == 0)
return -1;
if (element == NULL) {
*data = list->head->data;
old_element = list->head;
list->head = list->head->next;
if (list_size(list) == 1)
list->tail = NULL;
}
else {
if (element->next == NULL)
return -1;
*data = element->next->data;
old_element = element->next;
element->next = element->next->next;
if (element->next == NULL)
list->tail = element;
}
free(old_element);
list->size--;
return 0;
}
This file compiles as follows: >cl /LD list.c. Now here is the stack.c file:
#include <stdlib.h>
#include "list.h"
#include "stack.h"
int stack_push(Stack *stack, const void *data) {
return list_ins_next(stack, NULL, data);
}
int stack_pop(Stack *stack, void **data) {
return list_rem_next(stack, NULL, data);
}
This file, stack.c, compiles as a module (object file), with list.obj as a dependency. Why? The structure Stack is the stack data structure. One way to implement a stack is as a linked list. A simple way to do this is to typedef Stack to List. In addition to simplicity, using a typedef has the benefit of making the stack somewhat polymorphic. Informally, polymorphism is a principle normally associated with object-oriented languages that allows an object (a variable) of one type to be used in place of another. This means that because the stack is a linked list, and hence has the same properties as a linked list, we can use linked list operations on it in addition to those of a stack. Thus, the stack can behave like a linked list when we want it to. Below is the compilation:
c:\Program Files\Microsoft Visual Studio 9.0\VC\bin>cl /LD stack.c /link list.obj
Microsoft (R) 32-bit C/C++ Optimizing Compiler Version 15.00.30729.01 for 80x86
Copyright (C) Microsoft Corporation. All rights reserved.
stack.c
/out:stack.dll
/dll
/implib:stack.lib
list.obj
stack.obj
Here the main file, main_stack.c. It is broken down into parts that use the functions defined in the module (object, function-definition) files to solve the problem or perform the calculation:
#include <stdio.h>
#include <stdlib.h>
#include "list.h"
#include "stack.h"
static void print_stack(const Stack *stack) {
ListElmt *element;
int *data,
size,
i;
fprintf(stdout, "Stack size is %d\n", size = stack_size(stack));
i = 0;
element = list_head(stack);
while (i < size) {
data = list_data(element);
fprintf(stdout, "stack[%03d]=%03d\n", i, *data);
element = list_next(element);
i++;
}
return;
}
int main(int argc, char **argv) {
Stack stack;
int *data,
i;
stack_init(&stack, free);
fprintf(stdout, "Pushing 10 elements\n");
for (i = 0; i < 10; i++) {
if ((data = (int *)malloc(sizeof(int))) == NULL)
return 1;
*data = i + 1;
if (stack_push(&stack, data) != 0)
return 1;
}
print_stack(&stack);
fprintf(stdout, "Popping 5 elements\n");
for (i = 0; i < 5; i++) {
if (stack_pop(&stack, (void **)&data) == 0)
free(data);
else
return 1;
}
print_stack(&stack);
fprintf(stdout, "Pushing 100 and 200\n");
if ((data = (int *)malloc(sizeof(int))) == NULL)
return 1;
*data = 100;
if (stack_push(&stack, data) != 0)
return 1;
if ((data = (int *)malloc(sizeof(int))) == NULL)
return 1;
*data = 200;
if (stack_push(&stack, data) != 0)
return 1;
print_stack(&stack);
if ((data = stack_peek(&stack)) != NULL)
fprintf(stdout, "Peeking at the top element...Value=%03d\n", *data);
else
fprintf(stdout, "Peeking at the top element...Value=NULL\n");
print_stack(&stack);
fprintf(stdout, "Popping all elements\n");
while (stack_size(&stack) > 0) {
if (stack_pop(&stack, (void **)&data) == 0)
free(data);
}
if ((data = stack_peek(&stack)) != NULL)
fprintf(stdout, "Peeking at an empty stack...Value=%03d\n", *data);
else
fprintf(stdout, "Peeking at an empty stack...Value=NULL\n");
print_stack(&stack);
fprintf(stdout, "Destroying the stack\n");
stack_destroy(&stack);
return 0;
}
Here is how we compile these files, if we use the command line:
c:\Program Files\Microsoft Visual Studio 9.0\VC\bin>cl stack.c /link stacks.obj list.obj
main_stack.c
Microsoft (R) Incremental Linker Version 9.00.30729.01
Copyright (C) Microsoft Corporation. All rights reserved.
/out:main_stack.exe
stacks.obj
list.obj
main_stack.obj
Output:
Pushing 10 elements
Stack size is 10
stack[000]=010
stack[001]=009
stack[002]=008
stack[003]=007
stack[004]=006
stack[005]=005
stack[006]=004
stack[007]=003
stack[008]=002
stack[009]=001
Popping 5 elements
Stack size is 5
stack[000]=005
stack[001]=004
stack[002]=003
stack[003]=002
stack[004]=001
Pushing 100 and 200
Stack size is 7
stack[000]=200
stack[001]=100
stack[002]=005
stack[003]=004
stack[004]=003
stack[005]=002
stack[006]=001
Peeking at the top element...Value=200
Stack size is 7
stack[000]=200
stack[001]=100
stack[002]=005
stack[003]=004
stack[004]=003
stack[005]=002
stack[006]=001
Popping all elements
Peeking at an empty stack...Value=NULL
Stack size is 0
Destroying the stack
The most effective way to understand a queue is to visualize a line at a shopping store. As the line grows, shoppers are added at the tail. When the cashier finishes with a customer and becomes available, the head of the queue goes next. When we add a shopper to the tail, we "enqueue" it. When we remove a shopper from the head, we dequeue it. To write a queue, we use the list.h and the list.c files, along with three other files: a queue.h file, a queue.c file, and a main_queue.c file:
File:
#ifndef QUEUE_H
#define QUEUE_H
#include <stdlib.h>
#include "list.h"
typedef List Queue;
#define queue_init list_init
#define queue_destroy list_destroy
int queue_enqueue(Queue *queue, const void *data);
int queue_dequeue(Queue *queue, void **data);
#define queue_peek(queue) ((queue)->head == NULL ? NULL : (queue)->head->data)
#define queue_size list_size
#endif
And here is the queue.c file:
#include <stdlib.h>
#include "list.h"
#include "queue.h"
int queue_enqueue(Queue *queue, const void *data) {
return list_ins_next(queue, list_tail(queue), data);
}
int queue_dequeue(Queue *queue, void **data) {
return list_rem_next(queue, NULL, data);
}
The queue.c file compiles, again as a module, or as an object file. Of course, it does this using the list.obj file as a dependency. Afterwards, we need to write code to execute the functions defined in the header file and prototyped in the C source code file:
cl /LD queue.c /link list.obj
Now we can compile the main_queue.c file, having built these modules. Here is the main_queue.c file:
#include <stdio.h>
#include <stdlib.h>
#include "list.h"
#include "queue.h"
static void print_queue(const Queue *queue) {
ListElmt *element;
int *data,
size,
i;
fprintf(stdout, "Queue size is %d\n", size = queue_size(queue));
i = 0;
element = list_head(queue);
while (i < size) {
data = list_data(element);
fprintf(stdout, "queue[%03d]=%03d\n", i, *data);
element = list_next(element);
i++;
}
return;
}
int main(int argc, char **argv) {
Queue queue;
int *data,
i;
queue_init(&queue, free);
fprintf(stdout, "Enqueuing 10 elements\n");
for (i = 0; i < 10; i++) {
if ((data = (int *)malloc(sizeof(int))) == NULL)
return 1;
*data = i + 1;
if (queue_enqueue(&queue, data) != 0)
return 1;
}
print_queue(&queue);
fprintf(stdout, "Dequeuing 5 elements\n");
for (i = 0; i < 5; i++) {
if (queue_dequeue(&queue, (void **)&data) == 0)
free(data);
else
return 1;
}
print_queue(&queue);
fprintf(stdout, "Enqueuing 100 and 200\n");
if ((data = (int *)malloc(sizeof(int))) == NULL)
return 1;
*data = 100;
if (queue_enqueue(&queue, data) != 0)
return 1;
if ((data = (int *)malloc(sizeof(int))) == NULL)
return 1;
*data = 200;
if (queue_enqueue(&queue, data) != 0)
return 1;
print_queue(&queue);
if ((data = queue_peek(&queue)) != NULL)
fprintf(stdout, "Peeking at the head element...Value=%03d\n", *data);
else
fprintf(stdout, "Peeking at the head element...Value=NULL\n");
print_queue(&queue);
fprintf(stdout, "Dequeuing all elements\n");
while (queue_size(&queue) > 0) {
if (queue_dequeue(&queue, (void **)&data) == 0)
free(data);
}
if ((data = queue_peek(&queue)) != NULL)
fprintf(stdout, "Peeking at an empty queue...Value=%03d\n", *data);
else
fprintf(stdout, "Peeking at an empty queue...Value=NULL\n");
fprintf(stdout, "Destroying the queue\n");
queue_destroy(&queue);
return 0;
}
Here is how we compile these files: cl.exe main_queue /link list.obj queue.obj.
Here is the output:
Enqueuing 10 elements
Queue size is 10
queue[000]=001
queue[001]=002
queue[002]=003
queue[003]=004
queue[004]=005
queue[005]=006
queue[006]=007
queue[007]=008
queue[008]=009
queue[009]=010
Dequeuing 5 elements
Queue size is 5
queue[000]=006
queue[001]=007
queue[002]=008
queue[003]=009
queue[004]=010
Enqueuing 100 and 200
Queue size is 7
queue[000]=006
queue[001]=007
queue[002]=008
queue[003]=009
queue[004]=010
queue[005]=100
queue[006]=200
Peeking at the head element...Value=006
Queue size is 7
queue[000]=006
queue[001]=007
queue[002]=008
queue[003]=009
queue[004]=010
queue[005]=100
queue[006]=200
Dequeuing all elements
Peeking at an empty queue...Value=NULL
Destroying the queue
