Solving LCA by Reducing to RMQ in C#

• Download source - 3.68 KB

Introduction

I spent a bit of time yesterday looking for an algorithm to find the least common ancestor in a given tree. The LCA is the first node shared by two child nodes.

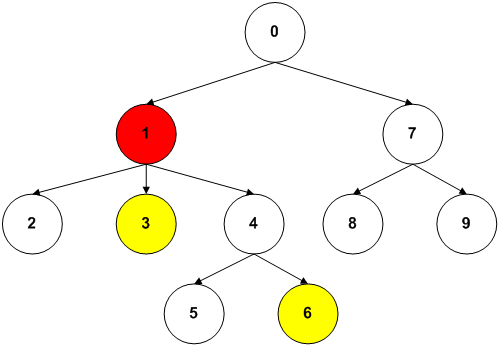
In the picture above, the least common ancestor for 3 and 6 is 1. The node 0 is also a common ancestor, but not the least common.

Least common ancestor has many applications for social networks, computer networks, common subexpression elimination in compilers, etc. My requirement is to find the common ancestor in an expression tree. I could not find anything on the internet in C#. I decided to write one based off of work by Robert Tarjan, Omer Berkman, and Uzi Vishkin.

A node in my graph has a value and a set of child nodes. We do not have a reference to the parent node. The only way to "identify" a node in this graph is by reference.

/// <summary>
/// A tree node.
/// </summary>
/// <typeparam name="T">The type of the value associated with this node.</typeparam>
public interface ITreeNode<T>
{
    /// <summary>
    /// Gets or sets the value.
    /// </summary>
    /// <value>The value.</value>
    T Value { get; set; }

    /// <summary>
    /// Gets the children.
    /// </summary>
    /// <value>The children.</value>
    IEnumerable<ITreeNode<T>> Children { get; }
}

Using the Code

We will create a helper class that has a single method. This method takes two nodes and returns their most common parent.

IGraphNode<T> FindCommonParent(ITreeNode<T> x, ITreeNode<T> y) 

The algorithm by Berkman and Vishkin is very straight forward. We do a bit of preprocessing first. We visit each node using Eulerian path and store this in an array. Eulerian path can be found using depth first transversal. We start at the root and record the path from the root to the first child. If that child also has a child node, then we record the path to that child all the way until we get to the bottom of the graph. Once we get to the bottom, we work our way up recording the path from the child back to the parent. If the parent has another child, we perform the same process until we have visited every node in the graph and made our way back up to the root.

private void PreProcess()
{
    // Eulerian path visit of graph 
    Stack<ProcessingState> lastNodeStack = new Stack<ProcessingState>();
    ProcessingState current = new ProcessingState(_rootNode);
    ITreeNode<T> next;
    lastNodeStack.Push(current);

    NodeIndex nodeIndex;
    int valueIndex;
    while (lastNodeStack.Count != 0)
    {
        current = lastNodeStack.Pop();
        if (!_indexLookup.TryGetValue(current.Value, out nodeIndex))
        {
            valueIndex = _nodes.Count;
            _nodes.Add(current.Value);
            _indexLookup[current.Value] = new NodeIndex(_values.Count, valueIndex);
        }
        else
        {
            valueIndex = nodeIndex.LookupIndex;
        }
        _values.Add(valueIndex);

        // If there is a next then push the current value on to the stack along with 
        // the current value.
        if (current.Next(out next))
        {
            lastNodeStack.Push(current);
            lastNodeStack.Push(new ProcessingState(next));
        }
    }
    _nodes.TrimExcess();
    _values.TrimExcess();
}

After the preprocessing is finished, we can start calculating the LCA by using Range Minimum Query. Range Minimum Query works exactly as it sounds. For a given range in an array, we need to find the minimum value. Our range is defined by the first time a node is visited. We do a hash table lookup to get this information for the given nodes followed by a simple FOR loop to find the minimum value in the given range. Not including the hashtable lookups, we can say the worst case time is O(n) where n is the number of nodes in the graph.

public ITreeNode<T> FindCommonParent(ITreeNode<T> x, ITreeNode<T> y)
        {
            // Find the first time the nodes were visited during preprocessing.
            NodeIndex nodeIndex;
            int indexX, indexY;
            if (!_indexLookup.TryGetValue(x, out nodeIndex))
            {
                throw new ArgumentException("The x node was not found in the graph.");
            }
            indexX = nodeIndex.FirstVisit;
            if (!_indexLookup.TryGetValue(y, out nodeIndex))
            {
                throw new ArgumentException("The y node was not found in the graph.");
            }
            indexY = nodeIndex.FirstVisit;

            // Adjust so X is less than Y
            int temp;
            if (indexY < indexX)
            {
                temp = indexX;
                indexX = indexY;
                indexY = temp;
            }

            // Find the lowest value.
            temp = int.MaxValue;
            for (int i = indexX; i < indexY; i++)
            {
                if (_values[i] < temp)
                {
                    temp = _values[i];
                }
            }
            return _nodes[temp];
        } 

Points of Interest

There is one small issue with this solution. If we are calculating the LCA for nodes X, Y and Y is descendant of X, then this solution will return X. For my requirement, this is not an issue but in some cases may want to return the immediate parent of X instead.

This was my first crack at this and I am not an algorithm expert. There are plenty of more optimal solutions for this problem. This solution has very little code and very simple to understand. Please let me know if you have any feedback.